Различные виды уравнения прямой

Глава 1 Прямая на плоскости

Каждая прямая на плоскости определяется линейным уравнением первой степени с двумя неизвестными. Обратно: каждое линейное уравнение первого порядка с двумя неизвестными определяет некоторую прямую на плоскости.

I Уравнение прямой с угловым коэффициентом имеет вид: 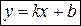, (1)

где - угловой коэффициент прямой (, где - угол, который прямая образует с положительным направлением оси ), - ордината точки пересечения прямой с осью (рисунок 1).

Рисунок 1

II Уравнение прямой, проходящей через данную точку в данном направлении: , (2)

где ( - угол, образуемый прямой с осью ); - координаты данной точки (рисунок 2).

Рисунок 2

III Уравнение прямой, проходящей через две данные точки и , где и имеет вид: (3)

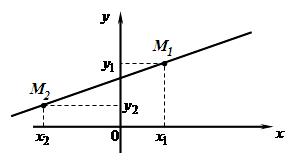
Рисунок 3

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

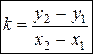(4)

Если , то уравнение прямой (3) имеет вид ;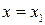

если , то: .

IV Общее уравнение прямой: , (5)

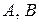где и 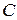- постоянные коэффициенты, причем 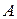и одновременно не обращаются в нуль (рисунок 4).

Рисунок 4

Заметим, что - нормальный вектор прямой ( перпендикулярен прямой). Частные случаи этого уравнения:

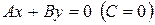- прямая проходит через начало координат (рисунок 5);

- прямая параллельная оси 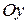(рисунок 6);

- прямая параллельна оси (рисунок 7);

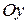- прямая совпадает с осью ;

- прямая совпадает с осью .

Рисунок 5 Рисунок 6 Рисунок 7

Уравнение прямой, проходящей через точку и нормальный вектор : (5)

Уравнение прямой в отрезках: 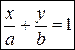, (5^/)

где и - длины отрезков (с учетом знаков), отсекаемых прямой на осях и соответственно () (рисунок 8).

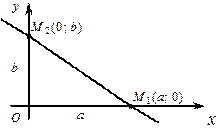Рисунок 8

V Каноническое уравнение прямой: , (6)

где - координаты точки лежащей на данной прямой и 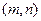- координаты направляющего вектора

Параметрическое уравнение прямой: , (6^/)

где - переменный параметр, .

В векторной форме уравнение (6^/) имеет вид , где , .

VI Нормальное уравнение прямой: 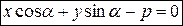, (7)

где 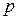- длина перпендикуляра, опущенного из начала координат на прямую, - угол, который этот перпендикуляр образует с положительным направлением оси (рисунок 9).

Общее уравнение прямой (5) можно преобразовать в нормальное уравнение (7) путем умножения на нормирующий множитель ; знак перед дробью берется противоположным знаку свободного члена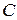

(в общем уравнении прямой).

Рисунок 9