
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перевірка
|
|
ПРАКТИЧНЕ ЗАНЯТТЯ № 1.
ТЕМА: «Обчислення визначників, формули Крамера.»
Індивідуальні завдання:
1. Обчислити визначник А (табл. 1):
а) за правилом трикутника; б) за правилом Саррюса; в) методом розкладання.
2. Обчисліть визначник В:
а) методом розкладання; б) методом зниження порядку;
в) методом зведення визначника до трикутного вигляду.
3. Обчисліть визначник С.
Таблиця 1.
| № | А | В | С | ||||||||||||||||||||||||||||||||||||||||||||||||||
| 1. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| 9. |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| 10. |
|
|
|
4. Розв'яжіть систему лінійних рівнянь методом Крамера:
| № | а) | б) |
| 1. | 
| 
|
| 2. | 
| 
|
| 3. | 
| 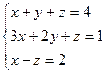
|
| 4. | 
| 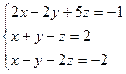
|
| 5. | 
| 
|
| 6. | 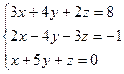
| 
|
| 7. | 
| 
|
| 8. | 
| 
|
| 9. | 
| 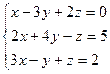
|
| 10. | 
| 
|
Зразки виконання завдань:
1. а) Обчислити визначник за правилом трикутників.
Розв’язання:

 .
.
б) Обчислити визначник за правилом Саррюса.
Розв’язання:

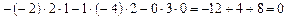 .
.
в) Обчислити визначник методом розкладання 
Розв’язання:
Обчислимо визначник шляхом розкладання його за елементами 3-го рядка, так як один елемент рядка дорівнює нулю,
.
2. Обчисліть визначник:
б)методом зниження порядку.
Розв’язання:

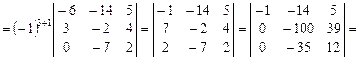

Для утворення нулів у рядку або стовпчику зручно мати розв’язувальний елемент, що дорівнює одиниці. Даний визначник такого елемента не має. Для його утворення можна, наприклад, помножити останній рядок визначника на –1 і додати до передостаннього, при цьому визначник не зміниться. У такий спосіб у третьому рядку утворилися три одиниці (достатньо мати одну). Для утворення нулів, наприклад у третьому рядку, можна взяти за розв’язувальний елемент одиницю, що стоїть на перетині першого стовпчика і третього рядка.
Помножимо елементи першого стовпчика спочатку на –1 і складемо з відповідними елементами другого стовпчика, тоді на місці елемента (3, 2) утвориться нуль. Далі множимо всі елементи того ж першого стовпчика на –3 і складаємо з елементами третього стовпчика. На місці елемента (3, 3) знову утворився нуль. У такий же спосіб, помноживши перший стовпчик на –1 і склавши з останнім, на місці елемента (3, 4) також утвориться нуль. Слід зазначити, що для утворення нулів у рядку працюють з елементами стовпчиків, а для утворення нулів у стовпчиках — з елементами рядків.
в) Обчислити визначник методом зведення до трикутного вигляду.
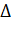 =
= 
Розв’язування.
Перший стовпчик визначника ненульовий, і в ньому на першому місці стоїть ненульовий елемент. Тому можна в першому стовпчику одержати нулі на всіх місцях, починаючи з другого. Для цього від другого рядка віднімаємо перший, помножений на 2:
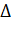 =
=  .
.
Далі від третього рядка віднімаємо перший, помножений на 3:
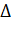 =
=  .
.
Від четвертого рядка віднімаємо перший, помножений на 2:
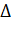 =
=  .
.
Нарешті від п’ятого рядка віднімемо перший:
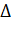 =
=  .
.
У другому стовпчику одержаного визначника на другом місці знаходиться ненульовий елемент. Тому одержуємо нулі у другому стовпчику на всіх місцях, починаючи з третього. Для цього від третього рядка віднімемо другий, від четвертого віднімемо другий, помножений на 11, і до п’ятого рядка додамо другий, помножений на 2.
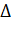 =
=  .
.
У третьому стовпчику одержаного визначника на другому місці знаходиться ненульовий елемент. Одержуємо нулі у третьому стовпчику, починаючи з четвертого місця. Для цього до четвертого рядка додамо третій помножений на 10, а від п’ятого віднімемо третій, помножений на 4
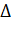 =
=  .
.
У даному визначнику четвертий елемент четвертого стовпчика не дорівнює нулю. Тому можна від п’ятого рядка відняти четвертий, помножений на  і одержати визначник трикутного вигляду відносно головної діагоналі
і одержати визначник трикутного вигляду відносно головної діагоналі
D =  .
.
Тоді D = 1× (-1)× 1× (-3)×  = 52
= 52
4. Розв’язати систему лінійних рівнянь методом Крамера:
а)  ; в)
; в)  .
.
а) Запишемо і обчислимо основний визначник системи:


Так як основний визначник системи відмінний від нуля, то система має єдиний розв’язок, який знайдемо за допомогою формул Крамера. Обчислимо допоміжні визначники 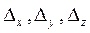 :
:

 ;
;

 ;
;

 ;
;
Використаємо формули Крамера: 
 ;
;  ;
; 
Перевірка
Підставимо знайдені  в ліві частини рівнянь заданої системи:
в ліві частини рівнянь заданої системи:
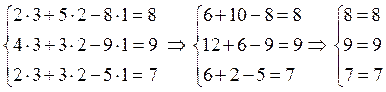
Сукупність чисел (3, 2, 1) являється єдиним розв`язком системи.
в) Запишемо і обчислимо основний визначник системи:

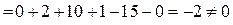
Так як основний визначник системи відмінний від нуля, то система має єдиний розв’язок, який знайдемо за допомогою формул Крамера. Обчислимо допоміжні визначники 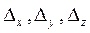 :
:

 ;
;

 ;
;


Використаємо формули Крамера: 
 ;
;  ;
; 