Краткое описание алгоритма Форда-Фалкерсона.

Формулировка цели и задачи.

Цель работы: изучение алгоритма нахождения максимального потока в двухполюсной сети.

Постановка задачи: нахождение реберно-независимых цепей между парой вершин (истоком и стоком) в графе с помощью алгоритма Форда-Фалкерсона.

Краткое описание алгоритма Форда-Фалкерсона.

Алгоритм начинается с произвольного потока из источника NS в сток NT. Алгоритм состоит в систематическом поиске всех возможных путей их NS в NT, увеличивающих поток (процесс расстановки пометок), и в соответствующем увеличении потока (процесс изменения потока).

ШАГ 1. Процесс расстановки пометок. На шаге 1 каждый узел находится в одном из трех состояний:

– " не помечен",

– " помечен и не просмотрен",

– " помечен и просмотрен".

Вначале все узлы не помечены. Пометка произвольного узла всегда состоит из двух частей. Первая часть – индекс узла Ni, который указывает, что можно послать поток из Ni в Nj. Вторая часть пометки – число, указывающее максимальную величину потока, который можно послать из источника NS в Nj, не нарушая ограничений на пропускные способности дуг. Прежде всего, источник NS получает пометку (S+, E(s)= ∞). Первая часть этой пометки означает, что можно послать поток из узла NS в этот узел; символ ∞ означает, что величина потока не ограничена сверху. Теперь узел NS " помечен и не просмотрен". А все остальные узлы " не помечены".

Выберем любой помеченный и не просмотренный узел Nj. Пусть он имеет пометку (i+, E(j)) или (i–, E(j)).

Два узла будем называть соседними, если они соединены дугой. Из всех узлов, соседних с Nj, выделим те узлы Nk, которые не помечены и для которых xjk < bjk.

Припишем каждому узлу Nk пометку (j+, E(k)), где E(k)=min { E(j), bjk – xjk }.

Такие узлы Nk теперь " помечены и не просмотрены". После этого всем соседним с Nj узлам Nk, которые не помечены и для которых xkj > 0, приписываем пометку (j–, E(k)), где E(k)=min { E(j), xkj }.

Такие узлы Nk теперь также " помечены и не просмотрены". Сейчас все узлы, соседние с Nj, имеют пометки. Тогда узел Nj считается помеченным и просмотренным, и его можно больше не рассматривать на этом шаге.

Может оказаться, что некоторые соседние с Nj узлы помечены, а остальные не могут быть помечены (либо все соседние с Nj узлы не могут быть помечены). В таких случаях узел Nj также считается помеченным и просмотренным. Знаки " + " и " – " в первой части пометок указывают, как должен меняться поток на шаге 2 (при знаке " + " увеличиваем поток, при знаке " – " уменьшаем поток).

Продолжим приписывать пометки узлам, которые являются соседними для помеченных и не просмотренных узлов до тех пор, пока либо узел NT окажется помеченным, либо нельзя будет больше пометить ни один узел и сток NT окажется непомеченным. Если NT не может быть помечен, то не существует пути из NS в NT, увеличивающего поток, и, следовательно, полученный поток максимален. Если же NT помечен, то на шаге 2 можно найти путь, увеличивающий поток.

ШАГ 2. Изменение потока. Предположим, что сток NT имеет пометку (k+, E(t)). Тогда заменим xkt на (xkt + E(t)). Если же он имеет пометку (k–, E(t)), то xkt заменим на (xkt –E (t)). Затем в любом из этих случаев переходим к узлу Nk. Вообще, если узел Nk имеет пометку (j+, E(k)), то xjk заменим на (xjk +E(t)), и перейдем к узлу Nj. Если узел Nk имеет пометку (j–, E(k)), то xkj заменим на (xkj – E(k)) и перейдем к узлу Nj. После этого сотрем все старые пометки узлов и вновь перейдем к шагу 1 следующей итерации. Количество итераций алгоритма зависит от числа реберно независимых путей в графе между истоком и стоком.

Описание с детализацией по шагам применение алгоритма Форда-Фалкерсона для нахождения реберно-независимых цепей для заданного варианта графа.

Число узлов коммутации проектируемой сети N=7+i(mod 4).

i=3 ( номер варианта).

N=7+1(mod 4)=8.

Построение ориентированного графа G=(V, R) с N вершинами и R множеством ребер:

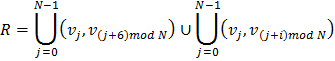
S = i mod N = 1

T = (i + 1)² mod N = 4

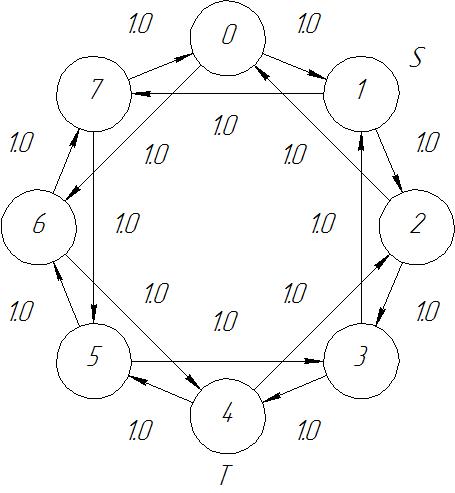
B_jk - пропускная способность дуги.

X_jk - текущий поток в дуге.

E(K)-величина потока в узле K

условие пометки (+)

b_jk-x_jk> 0

условие пометки (-)

x_jk> 0