Шаг 1(итерация 2). Расстановка пометок.

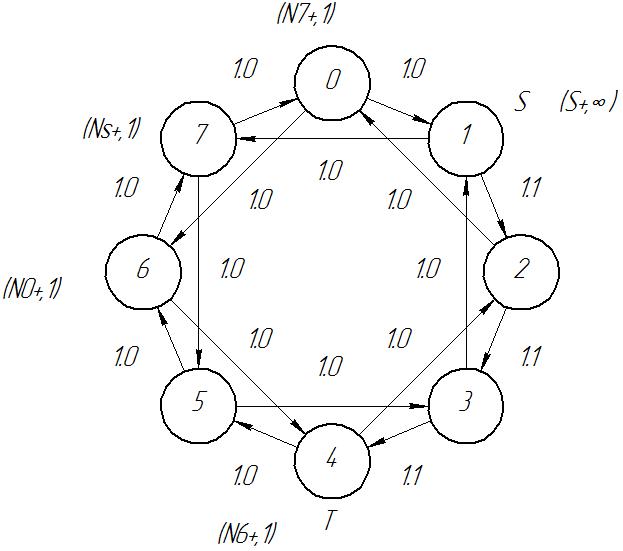
Приписываем узлу Ns пометку (S+, ∞). Узел Ns имеет 4 соседние непомеченные вершины: N0, N2, N3, N7. Узлы N0 и N3 пометить нельзя, так как Xij = 0. Узел N2 пометить так же нельзя, так как B_S2-X_S2=0. Пометим узел N7 как (S+, E(7)), где E(7)=min(E(s), B_S7-X_S7)=1.

Узел N7 имеет 3 соседние непомеченные вершины: N0, N5, N6. Узел N6 пометить нельзя, так как X₇₆=0. Пометим узел N0 как (N7+, E(0)), где E(0)=min(E(7), B₇₀-X₇₀)=1.

Узел N0 имеет 2 соседние непомеченные вершины: N2, N6. Узел N2 пометить нельзя, так как X₀₂=0. Пометим узел N6 как (N0+, E(6)), где E(6)=min(E(0), B₀₆-X₀₆)=1.

Узел N6 имеет 2 соседние непомеченные вершины: Nt, N5. Узел N5 пометить нельзя, так как X₆₅=0. Пометим узел Nt как (N6+, E(t)), где E(t)=min(E(6), B_6T-X_6T)=1. Так как узел Nt помечен, то переходим к шагу 2.

Шаг 2(итерация 2). Изменение потока.

Максимальный поток увеличен на E(t)=1.

Пометка N7 есть (Ns+, 1), увеличиваем X_S7 на 1. X^’_S7=X_S7+1=1.

Пометка N0 есть (N7+, 1), увеличиваем X₇₀ на 1. X^’₇₀=X₇₀+1=1.

Пометка N6 есть (N0+, 1), увеличиваем X₀₆ на 1. X^’₀₆=X₀₆+1=1.

Пометка Nt есть (N6+, 1), увеличиваем X_6T на 1. X^’_6T=X_6T+1=1.

Шаг 3.

Так как в графе больше нет реберно-независимых путей, алгоритм завершен.

Вывод:

С помощью алгоритма Форда-Фалкерсона между парой вершин S и T найдены 2 реберно-независимые цепи:

- (S-2), (2-3), (3-T).

- (S-7), (7-0), (0-6), (6-T).

Анализ результатов исследования заданного графа сети(ST-отделяющееся множество, ST-разделяющееся множество, разрез, пропускная способность и максимальный поток, обоснование выбора диаметра).

ST-разделяющим множеством называется множество A дуг графа, обладающее тем свойством, что любая дуга, принадлежащая всякой простой цепи из S в T, содержится в A.

ST-разделяющее множество A ={(S, 2), (2, 3), (3, T), (S, 7), (7, 5), (5, 3), (7, 0), (0, 6), (6, T), (5, 6), (2, 0}.

ST-отделяющим множеством называется множество B вершин графа (не содержащее S и T), обладающее тем свойством, что любая простая цепь из S в T, проходит через вершину из B и все вершины, через которые проходит всякая простая цепь S в T, включены в B.

ST-отделяющее множество B ={0, 2, 3, 5, 6, 7}.

Разрезом называется такое разделяющее множество, никакое собственное подмножество которого не является разделяющим.

Пропускной способностью разреза называется сумма пропускных способностей принадлежащих ему дуг.

Разрез {{S, N2}, {S, N7}} с пропускной способностью равной 2.

Диаметром графа называется максимальная длина кратчайших маршрутов в графе (максимум берется по всем парам вершин).

Диаметр

{N0-N1}-1

{N0-N2}-2

{N0-N3}-3

{N0-N4}-2

{N0-N5}-3

{N0-N6}-1

{N0-N7}-2

Диаметр = 4

Теорема 3 (Форда-Фалкерсона)

Если в сети существует цепь, идущая из Ns в Nt, то максимальный поток из Ns в Nt равен минимальной пропускной способности разрезов, разделяющих Ns и Nt.

Максимальный поток между истоком и стоком равен2.