
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Билет №1
|
|
Линейные дифференциальные уравнения n -ого порядка. Свойства их решений
В общем случае данные уравнения имеют вид  ,
,
где  - непрерывные функции.
- непрерывные функции.
Обозначим левую часть дифференциального уравнения, линейную относительно y и ее производных через  , т. е.
, т. е.
 . Тогда уравнение можно записать в виде
. Тогда уравнение можно записать в виде 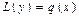 . Этому неоднородному уравнению соответствует однородное уравнение
. Этому неоднородному уравнению соответствует однородное уравнение  .
.
Свойство 1. Если  и
и  являются решениями однородного уравнения
являются решениями однородного уравнения  , то их сумма
, то их сумма  также является решением этого уравнения. Действительно, в силу линейности функции
также является решением этого уравнения. Действительно, в силу линейности функции 
 .
.
Свойство 2. Если  является решением уравнения
является решением уравнения  , то
, то  , где
, где  , также является решением этого уравнения.
, также является решением этого уравнения.
Свойство 3. Если  являются решениями уравнения
являются решениями уравнения  , то
, то  , где
, где  - постоянные также является решением этого уравнения.
- постоянные также является решением этого уравнения.
В силу линейности уравнения имеем  .
.
Свойство 4. Если  являются решениями однородного уравнения
являются решениями однородного уравнения  , а
, а  решением неоднородного уравнения
решением неоднородного уравнения  , то
, то  также является решением неоднородного уравнения.
также является решением неоднородного уравнения.