Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Московский Государственный Открытый Университет
|
|
Московский Государственный Открытый Университет
Губкинский институт (филиал МГОУ)
Курсовая работа
по “Теоретическим основам
электротехники”
курсовик выполнен верно!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Выполнил:
Студент 3 курса
горного факультета
гр. ГЭ-04
Шифр: 804314
Специальность: 140211
Панков А. И.
Проверил:
Богданов Виктор
Михайлович
Губкин
2007
Определение варианта к индивидуальному заданию.
ШИФР:
| А | Б | В | Г | Д | Е |
| Последняя цифра шифра | ||||||||||
| А | ||||||||||
| Б |
А-2; Б-3; В-1; Г-2; Д-3; Е-4.
Рассчитанный код:
| А | Б | Д | Г | В | Е |
| a | b | c | d | e | f |
ЗАДАНИЕ 1
Исходные данные.
В схеме каждая ветвь содержит источник ЭДС и резистивный элемент, а одна ветвь только источник тока.
Ecd=E(5-c) (5-e)=E32=E24=50 B.
E(5-c) (5-f)=E(5-f) (5-d)=E(5-d) (5-e)=E21=E13=E34=30 B.
Jab=J23=0, 9 A.
Rcd= Rdf= Rde=R32=R24=R21=80 Ом.
Rce =Rсf= Ref=R31=R34=R14=40 Ом.
Ief=I14=0, 6 A.
Eef=E14=?
Необходимо выполнить следующие пункты:
1. Начертить схему согласно исходным данным, соединяя зажимы ветвей, пронумерованные одинаково в один узел.
2. Произвести анализ схемы и определить число независимых уравнений Кирхгофа, составить и решить систему из этих уравнений.
3. Определить неизвестные токи и ЭДС, применив метод контурных токов.
4. Составить уравнение баланса мощности.
5. Считая известными все ЭДС и ток источника тока J23 определить ток в элементе R32, применив метод эквивалентного генератора,
попутно использовать метод узловых потенциалов и метод эквивалентных преобразований соединений резистивных элементов.
Решение.
1. Начертим схему согласно исходным данным.
2. Составим 3 уравнения по первому закону Кирхгофа и 3 уравнения по второму закону:
Подставив в систему уже известные значения, получаем:
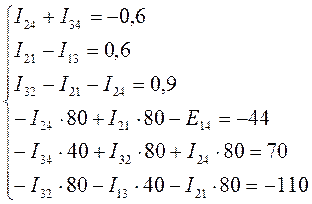
Решаем эту систему уравнений в Mathcad, получаем:
I24= -0, 302A; I34= -0, 298A; I21= 0, 431A; I13= -0, 169A;
I32= 1, 029A; E14= 102, 667B;
3. Заменяем две ветви одной эквивалентной:
Определяем неизвестные токи и ЭДС методом контурных токов.
Собственные сопротивления контуров:
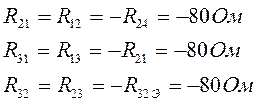
Контурные ЭДС:
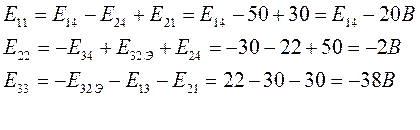
Составляем уравнения:
I11= I14=0, 6А
Решаем систему уравнений в Mathcad:
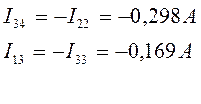
I24= -0, 302A; I34= -0, 298A; I21= 0, 431A; I13= -0, 169A;
I32= 1, 029A; E14= 102, 667B;
4. Составим уравнение баланса мощности:
Определим доставляемую источником тока мощность.
По закону Ома:
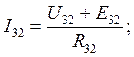
125, 95=125, 95
Следовательно, количество теплоты, выделяющейся в единицу времени в сопротивлениях схемы равняется энергии, доставляемой за тоже время источниками питания.
5. Рассчитаем j1, j2, j3 методом узловых потенциалов. При этом считаем, что ветвь, содержащая элемент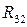 
разомкнута:
Заземляем 4 узел, т.е. j4=0.
Получим систему:
Решив ее, найдем j1, j2, j3.
Ток I32 найдем по формуле:
Определяем входное сопротивление всей схемы по отношению к зажимам 2 и 3 при закороченных источниках ЭДС. Считаем, что ветвь, содержащая источник тока J23 разомкнута.
Преобразуем треугольник в звезду:
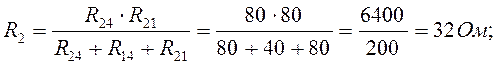
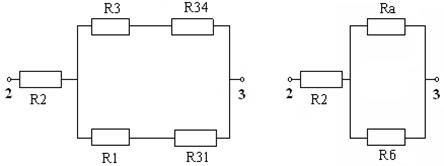
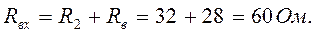
Определяем ток в элементе R32, применив метод эквивалентного генератора.
