
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическое обоснование. Эксперимент проводим над лампочками в количестве N=100 штук, со средним временем безотказной работы q =100 часов по плану [N,Б,T]
|
|
Эксперимент проводим над лампочками в количестве N=100 штук, со средним временем безотказной работы q =100 часов по плану [N, Б, T]. План типа [N, Б, T]- это эксперимент, при котором испытывается N элементов, каждый отказавший элемент не заменяется новым, а наблюдения ведутся до момента T.
Достаточной статистикой являются:
d(T)- число отказов за время T, и сумма времен, в течение которой проработал каждый элемент, т.е Sб- суммарная наработка элементов за время проведения испытаний.
Сгенерируем на всем временном интервале моменты отказов для 100 лампочек, распределенных по экспоненциальному закону с параметром
l = —
q
Последовательно просуммируем моменты отказов Σ ti, найдем
d(T)- число лампочек, отказавших за время Т. Затем вычислим суммарную наработку всех испытываемых элементов за время проведения эксперимента по формуле:
Sб=Σ ti + (N- d(T))T
С помощью соотношения
d(T)
l= ——
Sб
получим оценку lˆ.
Найдем смещение оценки lˆ по формуле:
Δ λ = lˆ - l
Для того чтобы определить, на сколько точно оценивается параметр l, повторим эксперимент 800 раз по описанному выше алгоритму. По полученным данным построим гистограмму и эмпирическую функцию для Δ l.
Вычислим математическое ожидание Δ l, т.е среднее арифметическое всех Δ l, по формуле:
Σ Δ l
MΔ l = ——
n
Данные действия выполним 10 раз при различных значениях Т(10, 20, 30, 40, 50, 60, 70, 80, 90, 100).
Построим график зависимости MΔ λ от времени T, на основе которого сделаем выводы о проведенном эксперименте.
5.5. Экспериментальные данные
Зададимся следующими параметрами:
Количество повторений опытов n=800
Количество элементов, над которыми проводится эксперимент N=100 лампочек
Среднее время работы одной лампочки θ =100 часов
Параметр экспоненциального распределения λ =1/100=0, 01
5.5.1. Зададим время проведения эксперимента Т=10 часов
На рис.1 приведена гистограмма распределения, на рис.2 приведена эмпирическая функция распределения оценки Δ l.
 Рис.1
Рис.1
|
| Гистограмма оценки l |
| Эмпирическая функция оценки l |
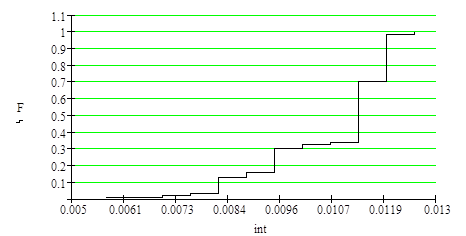 Рис.2
Рис.2
|
Математическое ожидание MΔ l = 0.011
5.5.2. Зададим время проведения эксперимента Т=20 часов
На рис.3 приведена гистограмма распределения, на рис.4 приведена эмпирическая функция распределения оценки l.
| Гистограмма оценки l |

|
Рис.3
| Эмпирическая функция оценки l |

|
Рис.4
Математическое ожидание MΔ l = 8.457 × 10-3
5.5.3. Зададим время проведения эксперимента Т=30 часов
На рис.5 приведена гистограмма распределения, на рис.6 приведена эмпирическая функция распределения оценки l.
| Гистограмма оценки l |
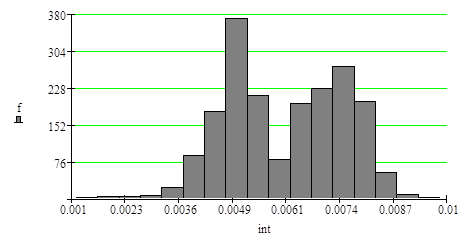
|
Рис.5
| Эмпирическая функция оценки l |

|
Рис.6
Математическое ожидание MΔ l = 6.061 × 10-3
5.5.4. Зададим время проведения эксперимента Т=40 часов
На рис.7 приведена гистограмма распределения, на рис.8 приведена эмпирическая функция распределения оценки l.
| Гистограмма оценки l |

|
Рис.7
| Эмпирическая функция оценки l |

|
Рис.8
Математическое ожидание MΔ l = 5.281 × 10-3
5.5.5. Зададим время проведения эксперимента Т=50 часов
На рис.9 приведена гистограмма распределения, на рис.10 приведена эмпирическая функция распределения оценки l.
| Гистограмма оценки l |

|
Рис.9
| Эмпирическая функция оценки l |

|
Рис.10
Математическое ожидание MΔ l = 4.05 × 10-3
5.5.6. Зададим время проведения эксперимента Т=60 часов
На рис.11 приведена гистограмма распределения, на рис.12 приведена эмпирическая функция распределения оценки l.
| Гистограмма оценки l |

|
Рис.11
| Эмпирическая функция оценки l |

|
Рис.12
Математическое ожидание MΔ l = 3.624 × 10-3
5.5.7. Зададим время проведения эксперимента Т=70 часов
На рис.13 приведена гистограмма распределения, на рис.14 приведена эмпирическая функция распределения оценки l.
| Гистограмма оценки l |
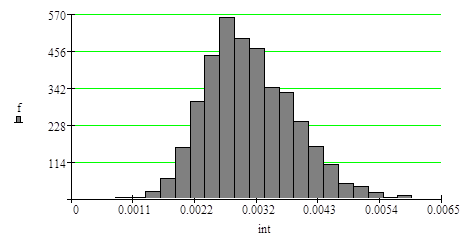
|
Рис.13
| Эмпирическая функция оценки l |
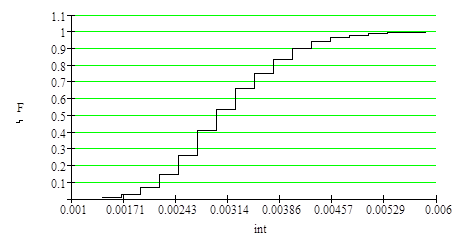
|
Рис.14
Математическое ожидание MΔ l = 3.118 × 10-3
5.5.8. Зададим время проведения эксперимента Т=80 часов
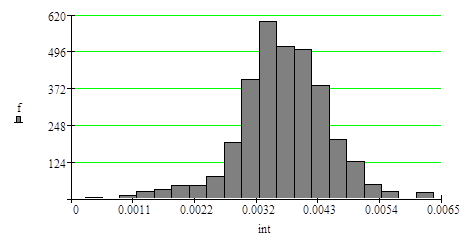
На рис.15 приведена гистограмма распределения, на рис.16 приведена эмпирическая функция распределения оценки l.
| Гистограмма оценки l |
|
Рис.15
| Эмпирическая функция оценки l |

|
Рис.16
Математическое ожидание MΔ l = 3.708 × 10-3
5.5.9. Зададим время проведения эксперимента Т=90 часов
На рис.17 приведена гистограмма распределения, на рис.18 приведена эмпирическая функция распределения оценки l.
| Гистограмма оценки l |

|
Рис.17
| Эмпирическая функция оценки l |

|
Рис.18
Математическое ожидание MΔ l = 3.054 × 10-3
5.5.10. Зададим время проведения эксперимента Т=100 часов
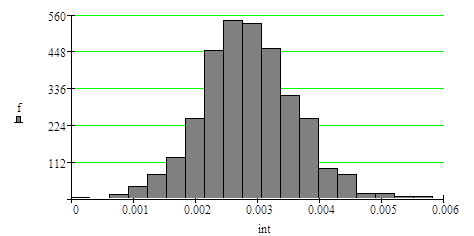
На рис.19 приведена гистограмма распределения, на рис.20 приведена эмпирическая функция распределения оценки l.
| Гистограмма оценки l |
|
Рис.19
| Эмпирическая функция оценки l |

|
Рис.20
Математическое ожидание MΔ l = 2.847 × 10-3
5.5.11. На основе найденных мат. ожиданий оценки Δ l можно построить график зависимости между средним значением оценки параметра l и временем наблюдения T, который представлен на Рис.21.
| График зависимости между Dl и T |

|
Рис.21
6. ЗАКЛЮЧЕНИЕ
Анализируя экспериментальные данные можно прийти к следующим выводам:
6.1. С увеличением времени усечения смещение оценки Δ l уменьшается. Максимальное значение математического ожидания смещения оценки параметра λ при повторении опыта 800 раз не превышает 0.011 (см. таблица 1). Это дает основание говорить о большой точности оценки l^.
Таблица1
| Время усечения T, часов. | Смещение оценки Δ l |
| T=10 | 0.011 |
| T=20 | 0.008457 |
| T=30 | 0.006061 |
| T=40 | 0.005281 |
| T=50 | 0.00405 |
| T=60 | 0.003624 |
| T=70 | 0.003118 |
| T=80 | 0.003708 |
| T=90 | 0.003054 |
| T=100 | 0.002847 |
Точность оценки l^ увеличивается. Это дает основание говорить о большой точности оценки. Данные заключения подтверждают экспериментальные данные, полученные в ходе исследования.
В реальной жизни нет возможности проводить эксперимент длительное время, поэтому компенсировать непродолжительность наблюдений можно увеличением числа одновременно испытываемых изделий. В ходе эксперимента использовалось 100 одновременно работающих лампочек, которые в последствие отказа не заменялись. Однако при увеличении количества лампочек можно получить более точные экспериментальные данные и лучшую точность оценки l^.
7. СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Вентцель Е.С. Теория вероятностей. М., 1969.
2. Бомас В.В., Булыгин В.С., Машкин М.Н. Теория вероятностей и математическая статистика: Лекции. М.: НПК “ Поток ”, 2000
- Гнеденко Б.В., ”Математические методы в теории надежности”
4. Кирьянов Д.В., Самоучитель Mathcad 11.- СПб.: БХВ-Петербург, 2003.
ПРИЛОЖЕНИЕ
| 4. Проведение эксперимента [N, Б, T]. Результаты счета |
| 4.1. Генерация моментов отказа |

|
| - Количество повторений опытов |

|
| - Количество элементов (100 лампочек) |

|
| - Среднее время работы одной лампочки |

|
| - Задаваемый параметр в экспоненциальном распределении |

|

|

|
| - Генерация интервалов между моментами отказов, подчиненных экспоненциальному закону |

|

|
| - Функция создания массива при усеченном наблюдении |
| 4.2. Оценка характеристик при T=100 |

|
| - Время проведения эксперимента |

|

|
| - Число элементов, отказавших за время T |

|
| - Суммарная наработка элементов за время Т |
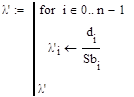
|
| - Вектор оценок l |

|
| - Вектор смещений |
| Построение гистограммы для оценок Dl |

|
| - Количество интервалов разбиения |

|
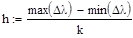
|
| - Расчет шага |
| - Расчет интервалов гистограммы |

|

|
| - Функция гистограммы |

|
| Гистограмма оценки Dl |

|
| Построение эмпирической функции |

|

|
| - Эмпирическая функция |
| Эмпирическая функция оценки Dl |

|

|

|
| - Расчет мат. ожидания оценки Dl |