
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нагрузочная характеристика.
|
|
Это зависимость U = f ( ) при I = const, cos φ = const и f 1 = fном, т.е. х.х.х. – это частный случай нагрузочной характеристики, когда I = 0.
) при I = const, cos φ = const и f 1 = fном, т.е. х.х.х. – это частный случай нагрузочной характеристики, когда I = 0.
Практический интерес представляет индуктивная нагрузочная характеристика, которая соответствует чисто индуктивной нагрузке СГ (cosφ =0).
Из векторной диаграммы видно, что  и
и 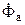 здесь складываются алгебраически, а
здесь складываются алгебраически, а 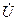 и
и  (
( ) – арифметически.
) – арифметически.
При этом I=Iн. Если положить, что ra =0, то векторная диаграмма будет иметь вид:

Рисунок 5.2.7 – Векторная диаграмма СГ в режиме индукционной характеристики
По характеристикам х.х. и индукционной нагрузочной, можно построить реактивныйтреугольник, вертикальный катет которого СВ равен падению напряжения в

Рисунок 5.2.8 – Построение реактивного треугольника
сопротивлении рассеяния Iнxσ a, а горизонтальный АВ равен н.с. реакции якоря в масштабе тока if, или kidIн.
Этот треугольник можно построить, если известны:
1) сопротивление рассеяния  ;
;
2) прямолинейная часть характеристики х.х.;
3) OA = if к – ток возбуждения при коротком замыкании, Iк = Iн, U =0, т.е. для точки А уравнение СГ:
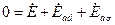 ; (ra =0) ; (ra =0)
| (5.2.13) |
Поскольку все три э.д.с. совпадают по фазе, то можно перейти к алгебре:
 , ,
| (5.2.14) |
т.е. при коротком замыкании ОА часть н.с. идёт на  (ОВ), а остаток – на
(ОВ), а остаток – на  .
.
Если известно 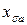 , то можно по х.х.х. найти if, необходимый для компенсации
, то можно по х.х.х. найти if, необходимый для компенсации  (ОВ). Следовательно АВ = ОА–ОВ – в масштабе if – н.с. р.я..
(ОВ). Следовательно АВ = ОА–ОВ – в масштабе if – н.с. р.я..
Поскольку  и
и  практически не зависят от
практически не зависят от 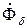 , то индуктивную нагрузочную характеристику можно построить по х.х.х., передвигая треугольник ОСА параллельно, причём точка С должна скользить по х.х.х..
, то индуктивную нагрузочную характеристику можно построить по х.х.х., передвигая треугольник ОСА параллельно, причём точка С должна скользить по х.х.х..
Для точки  ОК должна индуктировать
ОК должна индуктировать  . DK индуктирует
. DK индуктирует  ; OD -
; OD - 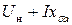 (
( ) – что и требовалось доказать.
) – что и требовалось доказать.
По двум характеристикам можно найти xσ a.
Из точки  отложить
отложить  , затем
, затем  параллельно ОС (найти точку
параллельно ОС (найти точку  ), потом
), потом
 , ,
| (5.2.15) |
кроме того, можно найти:
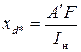 . .
| (5.2.16) |