Ошибки выборочного наблюдения.

Расхождения между показателями генеральной и выборочной совокупностей называются ошибками репрезентативности; они возникают потому, что выборочная совокупность не точно воспроизводит состав генеральной совокупности. Для средней величины ошибка является разницей между генеральною и выборочной средними; для части - разницей между генеральною и выборочной частями.

Предельная ошибка репрезентативност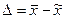и , или 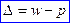, где w - часть исследуемого признака в генеральной совокупности, а p - часть исследуемого признака в выборочной совокупности).

Различаются:

- ошибки выборки;

- ошибки регистрации.

Ошибки регистрации возникают при неправильном установлении факта в процессе наблюдения. Они свойственны как сплошному наблюдению, так и выборочному, но в выборочном их меньше.

По природе ошибки бывают:

- систематические – преднамеренные, т.е. были отобраны либо лучшие, либо худшие единицы совокупности. При этом наблюдения теряют смысл;

- случайные – основной организационный принцип выборочного наблюдения состоит в том, чтобы не допустить преднамеренного отбора, т.е. обеспечить строгое соблюдение принципа случайного отбора.

В теории выборочного наблюдения существуют два метода отбора: повторный и бесповторный отбор. Сущность повторного отбора состоит в том, что каждая, попавшая в выборку единица, после наблюдения возвращается в генеральную совокупность и может быть исследована повторно. При повторном отборе средняя ошибка выборки рассчитывается:

На практике повторный отбор применяется редко. При бесповторном отборе, численность генеральной совокупности N в ходе выборки сокращается, формула средней ошибки выборки для количественного признака имеет вид:

, тогда

где - средняя ошибка выборки, которая характеризует степень отклонения выборочной средней от генеральной средней.

Вычислим средние ошибки по нашему примеру (табл. 2).

для повторного отбора

для бесповторного отбора

Вычисленные ошибки дают возможность определить пределы средней генеральной совокупности:

при повторном отборе:

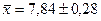
Для бесповторного отбора:

Средний процент естественных потерь в генеральной совокупности - в пределах от 7, 58 до 8, 1 %. Опираясь на теорию вероятностей, мы этот результат можем утверждать с вероятностью 0, 683, или только на 68, 3 %. То есть, если отобрать 1000 партий товара, то 683 из них будут иметь процент естественных потерь в вычисленных выше пределах.

Средняя ошибка части единиц, которые имеют определенные значения признака, вычисляется по формулам:

Для повторного отбора:

Для бесповторного отбора:

Вычислим для нашего примера (табл. 2) среднюю ошибку части:

Для повторного отбора:

Для бесповторного отбора:

Это свидетельствует, что часть продукции с естественными потерями свыше 10 % в выборочной совокупности отклоняется от части в генеральной совокупности на 4%. Т.е. часть в генеральной совокупности будет составлять:

Где можно утверждать с вероятностью 0, 683, то есть ошибка не превышает 1 . Такая вероятность часто не устраивает исследователей. Чтобы увеличить вероятность, нужно расширить пределы отклонений, принять за меру удвоенную ошибку выборки (2 ). В этом случае вероятность утверждения достигнет 0, 954, а средний процент естественных потерь уже будет в пределах:

= 0, 26%; 0, 26*2 = 0, 52%;

7, 58% ±0, 52%; 7, 06% 8, 10%.

Следовательно, часть признака будет находиться в пределах: = 4; 4 *2= 8; 10%±8%;

2 % 18 %.

Ошибка выборки, вычисленная с вероятностью больше чем 0, 683, называется в статистике предельной и вычисляется по формуле:

где - предельная ошибка; t - коэффициент доверия соответствует вероятности Р. На практике чаще всего используют такие вероятности:

0, 683 , при 0, 954 , при 0, 987 .

Исходя из того, что предельная ошибка выборки для вероятностей Р является максимальным отклонением распределения значений выборочной оценки от характеристики генеральной совокупности, возможные пределы значений генеральной средней и части определяют так:

Приведенные формулы дают возможность вычислить объем выборки, при котором отклонении выборочных показателей от генеральных не превысят заранее заданных размеров, с определенной вероятностью.