Основні види матриць.

– Матриці А і В називаються рівними, якщо всі їх відповідні елементи і рівні, тобто = . Отже, рівними можуть бути тільки матриці одної розмірності.

– Матриця, в якої число рядків дорівнює числу стовпців, називається квадратною.

– Матриця, у якої всього один рядок, називається матрицею-рядком (ковектором).

– Матриця, у якої всього один стовпець – матрицею-стовпцем (контравектором). Їх також називають вектор-рядком і вектор-стовпцем відповідно.

– Діагональною називається матриця, у якої всі елементи, що не належать головній діагоналі, рівні нулю.

– Одинична матриця – це діагональна матриця, у якої всі елементи головної діагоналі рівні 1. Позначається одинична матриця літерою E або I.

- одинична матриця третього порядку.

– Якщо всі елементи матриці, що знаходяться нижче або вище головної діагоналі, дорівнюють нулю, то матриця називається трикутною.

– Матрицю називають транспонованою до , якщо . Якщо матриця А розміром , то матриця має розміри .

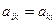– Якщо в має місце рівність , то матриця називається симетричною.

– Якщо , то називається антисиметричною. В антисиметричної матриці головна діагональ складається з нулів.

До кожної квадратної матриці розмірності можна скласти визначник . Його обчислюють за правилами, які розглянуті на лекції №1. Зазначимо, що прямокутна () матриця визначника не має.