
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Динамика. Основные законы механики. Колебательное движение материальной точки.
|
|
Динамика
Динамика – раздел механики, в котором изучаются законы движения материальных тел под действием сил. В динамике решаются два типа задач. Первая состоит в определении действующих сил при заданном законе движения материального объекта (точки или системы). Вторая задача обратная первой: определяется закон движения материального объекта при известных действующих на него силах.
Осн.законы механики (зак-ны Галилея-Ньютона):
Закон инерции (1-ый закон): материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит это состояние;
Инерция (инерционность) - свойство материальных тел, заключающееся в стремлении их сохранять неизменной скорость своего движения (или состояние покоя), т.е. сохранять данное кинематическое состояние.
Сила инерции материальной точки представляет собой противодействие материальной точки изменению ее скорости и приложена к телу, сообщающему этой точке ускорение. Сила инерции равна по модулю произведению массы материальной точки на модуль ее ускорения и направлена в сторону, противоположную ускорению  . При неравномерном криволинейном движении точки силу инерции, представленной в виде касательной (
. При неравномерном криволинейном движении точки силу инерции, представленной в виде касательной ( ), и нормальной (
), и нормальной (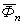 ) силами инерции. Эти силы направлены противоположно касательному и нормальному ускорению
) силами инерции. Эти силы направлены противоположно касательному и нормальному ускорению 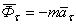 ,
, 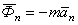 ,
, 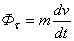 ,
, 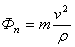 . В случае равномерного движения точки по кривой
. В случае равномерного движения точки по кривой 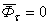 . В случае равномерного движения точки по прямой
. В случае равномерного движения точки по прямой  . Если точка принадлежит твердому телу, вращающемуся вокруг неподвижной оси, то модуль ее вращательной и центробежной сил инерции определяется по формулам:
. Если точка принадлежит твердому телу, вращающемуся вокруг неподвижной оси, то модуль ее вращательной и центробежной сил инерции определяется по формулам:  ,
,  , где
, где 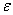 ,
,  — угловое ускорение и угловая скорость тела.
— угловое ускорение и угловая скорость тела.
Мерой инерции материальных тел являются: масса (при поступательном движении); момент инерции (при вращении).
Масса - количество материи данного вида в данной точке (в данном объеме) или количественная мера инерционности тела. Единица измерения массы - килограмм (кг).
Масса определяет инерционность тела только при поступательном движении, так как в этом случае скорости и ускорения всех точек тела в данный момент времени геометрически равны. При вращении вокруг оси инерционность тела определяется не только массой тела, но и тем как масса распределена окрест оси вращения. Чем компактнее (ближе к оси) распределена масса тела, тем меньше инерционность тела и наоборот. Поэтому при вращении тела вокруг оси его инерционность определяет момент инерции тела. Определяют моменты инерции тела относительно: точки (начала декартовой системы координат); оси (координатных осей); плоскости (координатных плоскостей).
Основной закон динамики (2-ой закон (Ньютона)): ускорение матер.точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление  ;
;
Законы инерции и пропорциональности силы и ускорения справедливы для инерциальных систем отсчета.
Система отсчета, в которой проявляются 1-ый и 2-ой законы, назыв. инерциальной системой отсчета. Для большинства задач за такую систему отсчета можно принять систему осей, связанных с Землей.
Закон равенства действия и противодействия (3-й закон (Ньютона)): всякому действию соответствует равное и противоположно направленное противодействие;
Закон независимости сил: несколько одновременно действующих на матер.точку сил сообщают точке такое ускорение, какое сообщила бы ей одна сила, равная их геометрической сумме. В классической механике масса движущегося тела принимается равной массе покоящегося тела, – мера инертности тела и его гравитационных свойств. Масса = весу тела, деленному на ускорение свободного падения.  , где g»9, 81м/с2. g зависит от географической широты места и высоты над уровнем моря – не постоянная величина, то в отличие от массы тела его вес не является постоянной величиной. Наибольший вес тело имеет на полюсе, а наименьший на экваторе.
, где g»9, 81м/с2. g зависит от географической широты места и высоты над уровнем моря – не постоянная величина, то в отличие от массы тела его вес не является постоянной величиной. Наибольший вес тело имеет на полюсе, а наименьший на экваторе.
Сила – 1Н (Ньютон) = 1кг× м/с2.
Дифференциальные уравнения движения материальной точки:  , в проекции на декартовы оси коорд.:
, в проекции на декартовы оси коорд.:  , на оси естественного трехгранника:
, на оси естественного трехгранника: 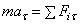 ;
;  ;
;  (
( – проекция ускорения на бинормаль), т.е.
– проекция ускорения на бинормаль), т.е.  (
( – радиус кривизны траектории в текущей точке). В случае плоского движения точки в полярных координатах:
– радиус кривизны траектории в текущей точке). В случае плоского движения точки в полярных координатах:  .
.
Две основные задачи динамики:
При решении этих задач исходными являются дифференциальные уравнения движения точки, записанные в общем виде в декартовых или естественных координатах.
Первая задача динамики – зная закон движения точки, определить действующую на нее силу;
Вторая задача динамики (основная) – зная действующие на точку силы, определить закон движения точки.
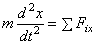 – дифференциальное ур-ие прямолинейного движения точки. Дважды интегрируя его, находим общее решение
– дифференциальное ур-ие прямолинейного движения точки. Дважды интегрируя его, находим общее решение  .
.
Постоянные интегрирования C 1, C 2 ищут из начальных условий: t =0, x = x 0,  =Vx=V0, x=f(t, x 0, V 0) – частное решение – закон движения точки.
=Vx=V0, x=f(t, x 0, V 0) – частное решение – закон движения точки.
Принцип относительности классической механики можно сформулировать так: никакие механические явления, происходящие в среде, не могут обнаружить ее прямолинейного и равномерного поступательного движения.
Материальная точка находится в состоянии относительного покоя, если геометрическая сумма приложенных к точке сил и переносной силы инерции равны нулю  .
.
Тела, падающие на землю, незначительно отклоняются от вертикали на восток за счет того, что сила инерции Кориолиса направлена на восток  , где
, где  — широта, на которой находится точка.
— широта, на которой находится точка.
Тело, брошенное вертикально вверх, отклоняется от вертикали на запад, т. к. сила инерции Кориолиса в этом случае направлена перпендикулярно плоскости меридиана к западу.
Состояние покоя механической системы. Состояние покоя механической системы может быть устойчивым, неустойчивым и безразличным.
Состояние покоя называется устойчивым, если система, выведенная из положения покоя, совершает малые колебания около этого положения.
Состояние покоя называется неустойчивым, если при сколь угодно малом отклонении из положения покоя система удаляется от этого положения.
Состояние называется безразличным, если при отклонении системы из положения покоя она и в новом положении может оставаться в состоянии покоя.
Критерий устойчивости состояния покоя механической системы, устанавливаемый теоремой Лагранжа — Дирихле.
Те положения покоя консервативной системы, в которых потенциальная система достигает минимума, являются ее устойчивыми состояниями покоя  .
.
Вид состояния покоя механической системы с одной степенью свободы в том случае, если 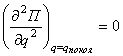 .
.
Если 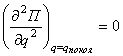 , необходимо вычислить последовательные производные
, необходимо вычислить последовательные производные  . Если первая не равная нулю производная имеет четный порядок и при этом положительна, то при
. Если первая не равная нулю производная имеет четный порядок и при этом положительна, то при 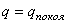 потенциальная энергия имеет минимум и устойчивое положение.
потенциальная энергия имеет минимум и устойчивое положение.