
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Библиографический список
|
|
1. Победря Б.Е., Георгиевский Д.В. Основы механики сплошной среды. - М., Физматлит, 2006 г.
2. Лойцянский Л.Г. Механика жидкости и газа. - М., Дрофа, 2003 г.
3. Механика жидкости и газа. Избранное. Под общей ред. Крайко А.Н. - М., Физматлит, 2003 г.
4. Винников В.А., Каркашадзе Г.Г. Гидромеханика. - М., МГГУ, 2003 г.
ЛАБОРАТОРНАЯ РАБОТА №3
ИССЛЕДОВАНИЕ ЗАКОНОМЕРНОСТЕЙ СТРУЙНОГО ПРИБОРА
1. ЦЕЛЬ РАБОТЫ
1. Исследовать экспериментально влияние отношения диаметров 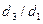 , формы входа в смеситель и взаимного расположения сопла и смесителя на кратность инжекции.
, формы входа в смеситель и взаимного расположения сопла и смесителя на кратность инжекции.
2. Сравнить кратность инжекции, полученную в опыте, с расчетной.
2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Струя, вытекающая из сопла в трубу, открытую с двух сторон, называется частично ограниченной. Вытекающая струя обладает большой скоростью и за счет трения (сцепления) непрерывно увлекает частицы окружающей среды по направлению потока.
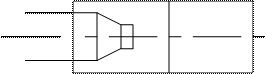
Свойство струи захватывать окружающую среду используют в струйных аппаратах. Простейший струйный аппарат состоит из сопла и смесителя (рис.27).

Рис.27. Схема струйного прибора и характер изменения пьезометрического давления по его длине:
1 - сопло; 2 – смеситель; 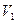 - рабочая среда;
- рабочая среда; 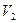 - подсасываемая среда;
- подсасываемая среда;  - смесь;
- смесь; 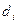 - диаметры;
- диаметры; 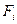 - площадь
- площадь
Из рис.27 видно, что при частичном ограничении струи происходит изменение пьезометрического давления по длине. На входе в смеситель создается разряжение, которое обеспечивает непрерывное поступление окружающей среды к началу смесителя. Возникает эффект всасывания. Этот эффект усиливается при установке конфузора. Конфузор также уменьшает потери при входе подсасываемой (инжектируемой) среды в смеситель.
В смеситель, в результате стесняющего влияния его стенок, происходит повышение пьезометрического давления.

Кратность m
Рис.28. Обеспечения максимального перепада давлений (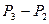 )
)
Чем больше повышение давления в смесителе, тем больше работа проталкивания, т.е. работа, необходимая для вытеснения потока из смесителя. Поэтому часто смеситель снабжается диффузором (расширяющейся насадкой) – устройством для повышения пьезометрического давления за счет снижения скоростного.
В зависимости от назначения струйные приборы называют либо инжекторами, либо эжекторами.
Инжектор - прибор для нагнетания какой – либо среды в рабочее пространство. Например, вовлечение окружающего воздуха в смеситель струей газообразного топлива и подача этой газо-воздушной смеси в печь.
Эжектор - прибор для отсасывания какой – либо среды. Например, сжатый воздух в качестве рабочего (эжектирующего) газа, за счет высокого разряжения перед смесителем, вовлекает продукты сгорания топлива из рабочего пространства печи в смеситель, а затем через диффузор удаляет их в атмосферу.
Основная характеристика работы струйного прибора –кратность инжекции (эжекции).
Кратность инжекции (эжекции) может быть объемная и массовая.
Объемная кратность инжекции(эжекции) характеризует отношение объемного расхода инжектируемой среды к объемному расходу рабочей среды.
 (1)
(1)
Массовая кратность инжекции (эжекции) характеризует отношение массового расхода инжектируемой среды к массовому расходу рабочей среды
 , (2)
, (2)
где  ;
;  - плотность среды;
- плотность среды;
Иногда кратность инжекции (эжекции) выражается как отношение объемного (массового) расхода смеси к объемному (массовому) расходу рабочей среды.
 ;
; 
Кратность инжекции (эжекции) зависит от отношения диаметров  , сопротивление на входе подсасываемой среды и от взаимного расположения сопла и смесителя. Отношение
, сопротивление на входе подсасываемой среды и от взаимного расположения сопла и смесителя. Отношение  при котором кратность инжекции достигает максимального значения, называется оптимальным. Сопротивление на входе подсасываемой среды можно уменьшить применением конфузора (см.рис.27). Существует также оптимальное расположение смесителя относительно сопла, при котором кратность инжекции (эжекции) максимальна. Расчет инжектора (эжектора) с целью определения его размеров
при котором кратность инжекции достигает максимального значения, называется оптимальным. Сопротивление на входе подсасываемой среды можно уменьшить применением конфузора (см.рис.27). Существует также оптимальное расположение смесителя относительно сопла, при котором кратность инжекции (эжекции) максимальна. Расчет инжектора (эжектора) с целью определения его размеров 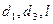 , производят путем решения уравнения энергетического баланса струйного прибора. Энергетический баланс струйного прибора представляет собой закон сохранения энергии: сумма кинетический энергий, подсасываемой и рабочей сред, расходуется на создание скорости смеси, потери на удар и работу проталкивания.
, производят путем решения уравнения энергетического баланса струйного прибора. Энергетический баланс струйного прибора представляет собой закон сохранения энергии: сумма кинетический энергий, подсасываемой и рабочей сред, расходуется на создание скорости смеси, потери на удар и работу проталкивания.
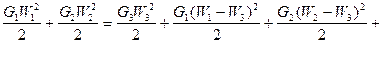
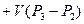 , (3)
, (3)
где  - массовые расходы рабочей, инжектируемой среды и смеси;
- массовые расходы рабочей, инжектируемой среды и смеси;
 - работа прокаливания (полезная);
- работа прокаливания (полезная);
 - объем смеси;
- объем смеси;
 - повышении давления в смесители;
- повышении давления в смесители;
Для удобства расчета инжектора (эжектора) уравнение (3) приводит к виду:  , (4)
, (4)
где  - объемная кратность инжекции (эжекции);
- объемная кратность инжекции (эжекции);
 - отношение плотностей газа инжектируемого к инжектирующей;
- отношение плотностей газа инжектируемого к инжектирующей;
 - отношение диаметров смесителя и сопла;
- отношение диаметров смесителя и сопла;
 - коэффициент, характеризующий работу противодавления (проталкивания);
- коэффициент, характеризующий работу противодавления (проталкивания);
 - повышения давления в смесителе, численно равно сумме потерь давления на трассе инжектируемого газа;
- повышения давления в смесителе, численно равно сумме потерь давления на трассе инжектируемого газа;
 - среднее скоростное давление инжектирующего газа на срезе сопла. Зная величину
- среднее скоростное давление инжектирующего газа на срезе сопла. Зная величину  и
и  потерь из уравнения (4), можно определить
потерь из уравнения (4), можно определить  - кратность инжекции, путем решения квадратного уравнения. Уравнение (4) представляют в виде:
- кратность инжекции, путем решения квадратного уравнения. Уравнение (4) представляют в виде:
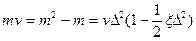 (5)
(5)
и решают относительно  .
.
Размеры струйного прибора зависят от его назначения. При малых значениях  приборы являются высоконапорными, создают значительный перепад по длине смесителя
приборы являются высоконапорными, создают значительный перепад по длине смесителя 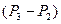 . Но при этом не могут обеспечить большую кратность инжекции (эжекции).
. Но при этом не могут обеспечить большую кратность инжекции (эжекции).
При большом значении  приборы обеспечивают значительную кратность инжекции (эжекции), но создают относительно небольшой перепад давления.
приборы обеспечивают значительную кратность инжекции (эжекции), но создают относительно небольшой перепад давления.
Если задана кратность инжекции (эжекции), то отношение  , обеспечивающее максимальный перепад давлений
, обеспечивающее максимальный перепад давлений 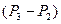 , можно определить по рис.28.
, можно определить по рис.28.
Геометрический параметры инжектора (эжектора) можно ориентировочно определить по рекомендациям Стельпроекта по рис.29.
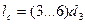 ;
;  ;
;  ;
;
угол раскрытия диффузора (6…9) град; угол сужения входного конфузора (30…45)град.
3. ОПИСАНИЕ УСТАНОВКИ
Установка для исследования струйного прибора представлена на рис.30. Рабочая среда (воздух)  подается от вентилятора через сопло 1. За счет разряжения окружающая среда
подается от вентилятора через сопло 1. За счет разряжения окружающая среда  подсасывается в смеситель 2. Из смесителя выходит смесь
подсасывается в смеситель 2. Из смесителя выходит смесь  .
.

Рис.29. Геометрический параметры инжектора

Рис.30. Схема установки:
1 - сопло; 2 – смеситель; 3 – трубка Прандтля;
4 – микроманометр; 5 – поворотная заслонка
Измерение скоростного давления на срезе сопла 1 и на срезе смесителя 2 производится с помощью пневматической трубки Прандтля 3, присоединенной к микроманометру 4. Предусмотрено перемещение трубки Прандтля вдоль и поперек оси струйного прибора. Регулирование расхода рабочей среды осуществляется поворотной заслонкой 5.
Установка включает три сменных смесителя, отличающихся диаметром и формой входа (см. рис. 30).
4. ПОРЯДОК ВЫПОЛНЕНИЕ РАБОТЫ
4.1. Ознакомиться с установкой.
4.2. Подготовить журнал наблюдений по форме (табл. 1, 2).
4.3. Произвести установку микроманометра по уровню, а жидкость по нулю. Синус угла наклона вначале сделать равным К=1, 0 и записать в журнал табл.1.
4.4. Трубку Прандтля, присоединенную к микроманометру, установить на срезе сопла по центру.
4.5. Включить вентилятор (включает лаборант или преподаватель).
4.6. Открыть поворотную заслонку 5.
4.7. Измерить максимальную скорость давления на срезе сопла ( ). Результата записать в соответствующую верхнюю строку журнала наблюдений (см. табл.1).
). Результата записать в соответствующую верхнюю строку журнала наблюдений (см. табл.1).
4.8. Трубку Прандтля удалить от сопла и установить смеситель 1 (при этом срез сопла совместить со срезом смесителя, а ось сопла должна совпадать с осью смесителя).
4.9. Подвести трубку Прандтля к срезу смесителя 1 и измерить скоростное давление по центру смесителя в его выходном сечении. Если величина давлений мала, то следует уменьшить “К” до 0, 5. Измеренное  по прибору, занести в журнал наблюдений (см.табл.1).
по прибору, занести в журнал наблюдений (см.табл.1).
4.10. Аналогичные измерения  произвести после установки смесителей 2 и 3. При установке срез смесителя на входе должен быть совмещен со срезом сопла (“нулевое” положение смесителя относительно сопла).
произвести после установки смесителей 2 и 3. При установке срез смесителя на входе должен быть совмещен со срезом сопла (“нулевое” положение смесителя относительно сопла).
4.11. Результаты, полученные со смесителя 2, перенести в табл. 2 в вариант установки “0”.
4.12. Переместить смеситель в положение “1” (-10 мм) (см. табл. 2 рисунок) и измерить также  на срезе смесителя по его центру. Результат занести в табл. 2 (вариант 1).
на срезе смесителя по его центру. Результат занести в табл. 2 (вариант 1).
4.13. Аналогичные измерения произвести для вариантов 2.3. Результаты занести в табл.2.
Примечание: Взаимное расположение сопла и смесителя.
 | |||
 | |||

 (-) (+)
(-) (+)
Перемещать смеситель через 10 мм влево (+), вправо (-).
5.1. Сделать перерасчет всех показаний  по прибору на истинные
по прибору на истинные  и записать а табл. 1 и 2 (
и записать а табл. 1 и 2 ( )
) 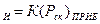 .
.
5.2. Подсчитать среднее скоростное давления:
а) на срезе сопла:
б) на срезе смесителя. При турбулентном движении среднее давление по сечению трубы  , измеренного по центру сечения. (
, измеренного по центру сечения. ( ) Результаты записать в соответствующие графы табл.1.2.
) Результаты записать в соответствующие графы табл.1.2.
5.3. Подготовить табл.3. “Обработка опытных данных” по прилагаемой форме, внести значение средних  и сделать необходимые расчеты, указанные в табл.3.
и сделать необходимые расчеты, указанные в табл.3.
5.4. По уравнению (5) определить расчетным путем объемную кратность инжекции (эжекции) для диаметра смесителя 70 и 90 мм (1 и 2). Величину 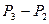 можно принять
можно принять  . Полученные данные занести в табл.3 и сравнить с опытными.
. Полученные данные занести в табл.3 и сравнить с опытными.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое частично ограниченная струя и каковы ее закономерности?
2. Каков характер изменения пьезометрического давления по длине смесителя.
3. Назначение диффузора на выходе и конфузора потока в струйном приборе?
4. Чем отличается инжектор от эжектора? Их назначение?
5. Что называется объемной и массовой кратностью инжекции (эжекции)?
6. От каких параметров и каким образом зависит кратность инжекции (эжекции) струйного прибора?
7. К чему сводится расчет инжекции (эжекции)?
8. Какое уравнение позволяет произвести расчет инжектора, какие величины оно связывает?
Таблица 1
Журнал наблюдений № 1
Влияние диаметров смесителя и формы входа на “  ”
”
| Место установки трубки Прандтля | Скоростное давле-ние Рск по центру сопла смесителя | 
| Среднее

| |
| На срезе сопла d = 20мм | . По приб | |||
| Истин | ||||
| №1 d=90 мм | По приб | |||
| Истин | ||||
| №2 d= 70 мм | По приб | |||
| Истин | ||||
| №3 (с конфузором) d= 70 мм | По приб | |||
| Истин |
Таблица 2
Журнал наблюдений №2
Влияние положения смесителя относительно сопла на “  ”
”
| Место установки трубки Прандтля | Вариант установки смесителя | Скоростное давление по центру смесителей №2/№3 |

| Среднее

| |
| На срезе смесителя №2/№3 d= 70 мм d=90 мм | По приб | ||||
| Истин | |||||
| (-10) | По приб | ||||
| Истин | |||||
| (+10) | По приб | ||||
| Истин | |||||
| (+20) | По приб | ||||
| Истин |
Таблица №3
Обработка опытных данных
| Параметры | Единицы измерения | На срезе сопла d = 20мм | На выходном срезе смесителя | На выходном срезе смесителя | |||||
| №1 d = 90мм | №2 d = 70мм (с конф) | №3 d = 70мм | 0 (0) | 1 (+10) | 2 (-10) | 3 (+20) | |||
Среднее скоростное давление 
| Н/м2 | ||||||||
Скорость, м/с
W = 1, 27 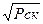
| м/с | ||||||||
Площадь сечения  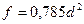
| м2 | ||||||||
Объемный расход 
| м3 /с | ||||||||
Опытная кратность 
| |||||||||
| Расчетная кратность по уравнению 5 | |||||||||
ЛАБОРАТОРНАЯ РАБОТА №4
ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ
1. Цель работы
1.1. Определить величину потери давления газа при выходе из сопла.
1.2. Определить коэффициент гидравлического сопротивления и построить график Eu=f(Re)
1.3. Определить коэффициент расхода газа μ.
1.4. Определить расход газа через сопло при различных пьезометрических давлениях.
1.5. Построить график зависимости V=f(P).
2. Теоретическая часть
Основное уравнение гидродинамики – уравнение Бернулли – широко используется в инженерной практике для решения технических задач. На его основе проводят расчеты трубопроводов и газоходов, насосных установок и гидравлических турбин. Принцип работы многих измерительных приборов также основан на использовании уравнения Бернулли: особо широкое применение находят приборы для измерения скоростей и расходов жидкости.
Закон (уравнение) Д.Бернулли есть частный случай закона сохранения энергии.
«Для установившегося течения идеальной несжимаемой жидкости сумма пьезометрического, геометрического и скоростного давлений (напоров) есть величина постоянная, равная полному давлению (напору) потока в данном сечении», т.е.
Рпьез + Ргеом + Рск = Рпол = const
или Рпьез + ρ qz + (pw² /2) = Рпол = const. (1)
где Рпьез – абсолютное пьезометрическое давление, Н/м² или (Па):
ρ qz – абсолютное геометрическое давление, Н/м² (Па):
(pw² /2) – абсолютное скоростное давление, Н/м² (Па).
Каждое давление есть соответствующая энергия (кинетическая, потенциальная положения или давления), отнесенная к 1 м³ жидкости (газа).
Разделив каждое слагаемое в уравнении (1) на pq, получим запись уравнения Бернулли в форме суммы соответствующих напоров.

(2)
где (Рпьез/pq), z, (w² /2q) – соответственно пьезометрический, геометрический и скоростной напоры, м.
Пьезометрический, геометрический и скоростной напоры – это соответствующие виды энергии отнесенные к 1 кг жидкости (газа).
Необходимо помнить, что в уравнениях (1) и (2) скорости соответствуют средним значениям скоростей в потоке жидкости.
 При движении реальной жидкости вследствие трения и вихревых движений часть механической энергии жидкости переходит в теплоту и рассеивается. Поэтому для составления уравнения Бернулли для двух выбранных сечений реальной жидкости при установившемся движении необходимо в правую часть уравнения добавить потерянную энергию. Тогда уравнение Бернулли для реальной жидкости имеет вид
При движении реальной жидкости вследствие трения и вихревых движений часть механической энергии жидкости переходит в теплоту и рассеивается. Поэтому для составления уравнения Бернулли для двух выбранных сечений реальной жидкости при установившемся движении необходимо в правую часть уравнения добавить потерянную энергию. Тогда уравнение Бернулли для реальной жидкости имеет вид
(3)
Уравнение (3) позволяет определить потери давления на участке трубопровода от сечения 1 до сечения 2 экспериментальным путем
Рпот = Р1 пол – Р2 пол. (4)
Таким образом, уравнение (4) указывает на одно из практических применений уравнения Бернулли, так как нахождение потерь давления и напора по газовому и водяному тракту является важнейшей задачей гидрогазодинамики.
Для иллюстрации уравнения (4) поместим в двух разных сечениях потока Г-образные трубки – трубки Пито, установив их навстречу потоку жидкости (рис. 1). Тогда трубки Пито укажут на полное давление в данных точках потока.

Рис. 31. Измерение полных давлений в сечениях 1 и 2
Уравнение Бернулли можно также применять для определения скорости истечения несжимаемой жидкости из объема через отверстие (сопло). А, следовательно, и для определения расхода жидкости 
Рис.3 2. Истечение несжимаемой жидкости через сопло
Жидкость считается несжимаемой, если в процессе движения ее плотность не меняется или меняется незначительно, т.е. p=const. В подавляющем большинстве случаев капельные жидкости считается несжимаемыми. Для газообразных сред при относительно невысоких скоростях и небольших перепадах давления (до 1000 Па) уравнение Бернулли также является справедливым. Эти условия характерны для движения газа в рабочем пространстве печей и дымовых каналов (боровах).
Запишем уравнение Бернулли для случая истечения газа из сопла (рис. 32), учитывая, что линии тока при приближении к отверстию искривляются, струя сжимается и это сжатие продолжается и становится максимальным на расстоянии ≈ 0.5d от среза сопла.
Отношение площади сечения сжатой струи fс к площади отверстия fо называется к о э ф ф и ц и е н т о м с ж а т и я струи
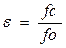
Полагая, что разность геометрических давлений в сечениях 1 и 2 равна нулю, т.к. поток горизонтален, запишем

(6)

где-потерянное скоростное давление, Па.
 Из уравнения (6) можно определить скорость потока в самом узком сечении
Из уравнения (6) можно определить скорость потока в самом узком сечении
(7)

 С учетом того, что
С учетом того, что
уравнение (7) примет вид

(8)
где φ – коэффициент скорости, который представляет собой
отношение

(9)
действительной скорости истечения к теоретической: он учитывает местное гидравлическое сопротивление и неравномерность распределения скоростей в самом узком сечении.
 |
Расход жидкости, вытекающей из отверстия, применительно к самому узкому сечению струи найдем из уравнения неразрывности (сплошности) потока:
 м3/c
м3/c
Измеренные значения перепада давления (мм вод.ст.) перевести в единицы системы СИ (Н/м²) (табл.1)
Таблица 1
Журнал наблюдений
| Пьезометрическое давление в сечениях | Полное давление в сечениях | |||||||
| По прибору, мм вод. ст. | нН/м² | по прибору, мм вод. ст. | нН Н/м² | по прибору, мм вод. ст. | Н/м² | По прибору , мм вод. ст. | Н/м² | |
| Температура воздуха в лаборатории t. °С - |
5. Обработка опытных данных
5. 1. Подготовить табл.2 «Результаты расчетов по опытным данным».
5. 2. Вычислить скоростные давления в сечениях 1 и 2 для каждого замера
 |
Если Р пьез < Р атм, то Р ск > Р пол.
 |
5. 3. Вычислить потери давления
Таблица 2
Результаты расчетов по опытным данным
| N№ П пп | Скоростное давление в сечениях | Потери давления, Р Н/м² | Коэффици-ент сопро- Тивления ξ | Коэффициент скорости φ | Расход воздуха м³ /с | Критерии | Плотность воздуха кг/м³ | |||
| Эйлера Eu | Рейнольд- са Re | |||||||||
 |
5. 4. Вычислить коэффициент гидравлического сопротивления
5. 5. Рассчитать плотность воздуха при температуре Тв.
 |
5. 6. Из уравнения (8) определить коэффициент скорости
5. 7. Найти среднее значение коэффициента скорости
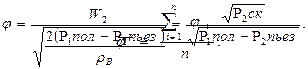 |
где n - число значений φ i.
Так как коэффициент сжатия ε ≈ 1, можно принять
 |
5. 8. Определить объемные расходы воздуха, вытекающего из сопла
 |
где f3 = 0.785d² = 0.785 * 0.02 = 0/000314 м² - площадь выходного сечения сопла.
5. 9. Определить действительную скорость для каждого опыта из уравнения расхода
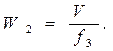 |
5. 10. Вычислить числа подобия Эйлера Eu и Рейнольдса Re, если критерий Re изменяется, а критерий Эйлера Eu остаётся постоянным, то наступает режим автомодельности.
 |
где d – диаметр сопла, d =0, 02 м:
u – коэффициент кинематической вязкости воздуха,
 |
5. 11. Результаты расчетов за
нести в табл. 2.
5. 12. По результатам расчетов построить графическую зависимость V = f (P2 cк), а также зависимость Eu = f (Re).
5. 13. В выводах указать:
- каким образом зависят потери давления от расхода жидкости (газа):
- какова величина коэффициента
- наблюдается ли автомодельность в рассматриваемом диапазоне расходов:
- как зависит расход жидкости через сопло от пьезометрического давления перед соплом.
Контрольные вопросы
1. Формулировка и физический смысл закона Бернулли.
2. Примеры практического применения уравнения Бернулли.
3. Что такое коэффициент сжатия струи? Коэффициент скорости? Коэффициент расхода?
4. Физический смысл коэффициента гидравлического сопротивления.
5. Что такое автомодельность потока? Когда она поступает в потоке жидкости?
6. Физический смысл чисел подобия Эйлера и Рейнольдса.
7. Как изменятся потери давления в трубопроводе при увеличении расхода жидкости (газа) вдвое?
Литература
1. Кривандин В.А., Марков Б.Л. Металлургические печи. –М.: Металлургия, 1977.
2.Теория, конструкции и расчеты металлургических печей: В 2-х томах. Т.1. Кривандин В.А., Филимонов Ю.П. Теория и конструкции металлургических печей. –М.: Металлургия, 1986.
3. Металлургическая теплотехника / В.А..Арутюнов, Б.С.Мастрюков и др. –М.: Металлургия, 1986
4. Абрамович Г.Н. Прикладная газовая динамика. –М.: Металлургия, 1969.