
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Умное число передает».
|
|
Николай Гумилев, «Слово»
Далее я практически дословно привожу описание модели «жертва–хищник», данное Владимиром Игоревичем Арнольдом в брошюре[434] «Жесткие» и «мягкие» математические модели». Брошюра представляет собой текст доклада, прочитанного академиком в 1997 г. на семинаре при президентском совете РФ. Целью доклада было рассказать чиновникам о применениях теории дифференциальных уравнений в таких науках, как экология, экономика и социология.
Моделью «жертва–хищник» принято называть знаменитую модель Лотки–Вольтерры, систему двух дифференциальных уравнений первой степени, описывающую борьбу за существование двух популяций, одна из которых является для другой пищевым ресурсом:
dX/dt = a * X – c * X * Y,
dY/dt = – b * Y + m * X * Y, [1]
где dX/dt, dY/dt – соответственно производные от X и Y по времени;
X – число карасей;
Y – число щук (желающие могут считать, что X – трудящиеся, а Y – бандиты, члены ОПГ).
Коэффициент «a» описывает скорость естественного прироста числа карасей в отсутствие щук, коэффициент «b» – естественное вымирание щук, лишенных карасей. Что означает, что среда стационарна и в неограниченном количестве обеспечивает всем необходимым для жизни один из видов (карасей), который мы называем «жертвой». Другой вид – «хищник» также находится в стационарных условиях, но питается лишь особями первого вида.
Вероятность взаимодействия (встречи) карася и щуки считается пропорциональной как количеству карасей, так и числу щук (учитывается в членах уравнений, содержащих произведение «X * Y»). Каждый акт взаимодействия уменьшает популяцию карасей (член «– c * X * Y» в правой части первого уравнения), но способствует увеличению популяции щук (член «+ m * X * Y» в правой части второго уравнения).
Модель Лотки–Вольтерры не обладает свойством структурной устойчивости, поскольку малые изменения описывающих модель параметров и функций существенно влияют на решения приведенных уравнений. Математический анализ этой (жесткой) модели показывает, что имеется стационарное состояние (A), всякое же другое начальное состояние (например, Б) приводит к периодическому колебанию численности как карасей, так и щук, так что по прошествии некоторого времени их количество возвращается к первоначальному состоянию в точке Б (рис. 19а, б).
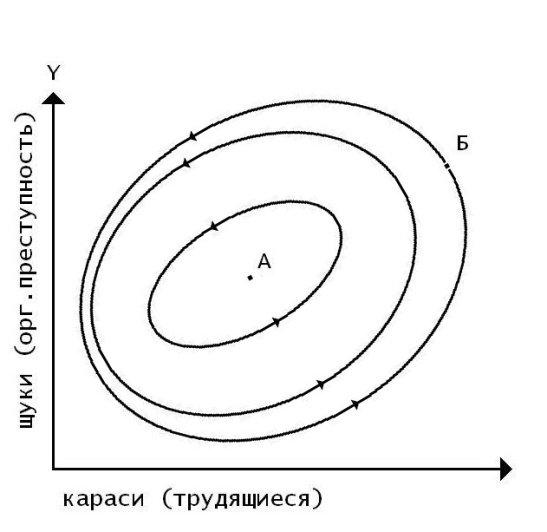
Рис. 19а. Вариант решения СДУ Лотки–Вольтерры – периодические колебания

Рис. 19б. Вариант решения СДУ Лотки–Вольтерры – периодические колебания (одно из семейства решений, показанных на рис. 19а)
При введении в модель малых изменений
dX/dt = a * X – c * X * Y + E * f(X, Y),
dY/dt = – b * Y + m * X * Y + E * g(X, Y), [2]
где E < < 1,
к правым частям уравнений добавляются малые члены (учитывающие, например, конкуренцию карасей за пищу и щук за карасей). В результате вывод о цикличности системы (о периодическом возвращении ее в исходное состояние Б), справедливый для первоначальной, жесткой системы Лотки–Вольтерры, теряет силу. В зависимости от вида малых поправок «f(X, Y)» и «g(X, Y)» возможны, например, уже структурно устойчивые сценарии, изображенные на рис. 20а, б, в.

Рис. 20а. Структурно устойчивый вариант решения СДУ Лотки–Вольтерры – сходящиеся траектории
В случае, изображенном на рис. 20а, равновесное состояние A устойчиво. При любых других начальных условиях (например, из точки Б) система через достаточно большой промежуток времени вернется в это устойчивое положение.
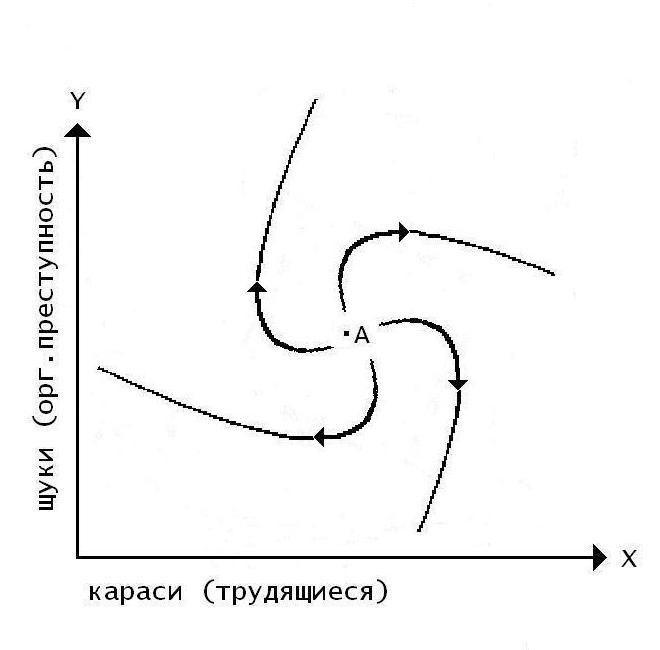
Рис. 20б. Структурно устойчивый вариант решения СДУ Лотки–Вольтерры – расходящиеся траектории
В случае, изображенном на рис. 20б, система «идет вразнос». Стационарное состояние неустойчиво, и малейшее отклонение от него может привести как к резкому увеличению числа бандитов, так и к их почти полному исчезновению (в том случае, когда трудящиеся настолько обездолены, что с них уже нечего взять, и между «братками» вспыхивают «браткоубийственные» войны). Такая система в конце концов попадает в область столь больших или столь малых значений X и Y, что модель выходит за границы своей применимости – эволюция переходит в революцию.
Комментарий.
Отдадим должное тонкому юмору академика.
Выступивший перед высоким начальством Владимир Игоревич по понятным причинам говорил о народе и бандитах, а также о том, что, согласно изложенной модели, в результате засилья бандитов происходит революция. Вряд ли кто из присутствовавших номенклатурных шишек (современный аналог «родовой знати» и высшего чиновничества, названных А. С. Пушкиным два века назад «светской чернью») понял, что указанные решения системы дифференциальных уравнений (СДУ) описывают текущую действительность, стоит лишь заменить слово «бандит» эквивалентным в нашей стране словом «чиновник».

Рис. 20в. Структурно устойчивый вариант решения СДУ Лотки–Вольтерры – траектории сходятся к движению по замкнутой кривой
В случае, изображенном на рис. 20в, в системе с неустойчивым стационарным состоянием A с течением времени устанавливается периодический режим C (подобный показанному на рис.19а). В отличие от исходной жесткой модели Лотки–Вольтерры, в этой модели установившийся периодический режим не зависит от начальных условий. Любое отклонение от стационарного состояния A приводит не к семейству колебаний вокруг A, а к колебанию вполне определенной (и не зависящей от значения отклонения) амплитуды. Возможны и другие структурно устойчивые сценарии (например, с несколькими периодическими режимами).
В заключение академик Арнольд дает ряд рекомендаций, которые мы приводим дословно:
«Вывод: жесткую модель всегда надлежит исследовать на структурную устойчивость полученных при ее изучении результатов по отношению к малым изменениям модели (делающим ее мягкой).
В случае модели Лотки–Вольтерры для суждения о том, какой же из сценариев 1–3 (или иных возможных) реализуется в данной системе, совершенно необходима дополнительная информация о системе (о виде малых поправок f и g в нашей формуле).
Математическая теория мягких моделей указывает, какую именно информацию для этого нужно иметь. Без этой информации жесткая модель может привести к качественно ошибочным предсказаниям. Доверять выводам, сделанным на основании жесткой модели, можно лишь тогда, когда они подтверждаются исследованием их структурной устойчивости».
Динамика дуальной пары Власть–Народ подробнее, точнее модели Лотки–Вольтерры описывается моделью структурно-демографических циклов[435], согласно которой «основная сила, разрушающая государство, – рост населения, ведущий к постепенному падению душевого дохода, пока в конечном итоге излишек сверх голодного существования становится недостаточным, чтобы удовлетворить правящий класс»[436]. О том же другими словами – в приведенной нами в начале первого Шага на третьей Ступени цитате из статьи Владимира Баранова: начальство подобно саранче, которая, сожрав все доступные ей пищевые ресурсы, в итоге сама начинает подыхать с голоду.
В результате структурно-демографического моделирования получается «…петля связей: рост населения → увеличение расходов государства → быстрый рост численности элиты → превышение несущей способности занимаемой территории → кризис элиты → развал государства → резкое сокращение населения. В соответствии с моделью эта цепочка дает колебания с периодом 200–300 лет. При наличии ресурсов может начаться новый цикл...»[437]
Нашей задачей, как вы понимаете, является поиск иного способа сосуществования граждан, не приводящий к периодическому развалу государства.
Заметка на полях.
Если быть до конца точным, структурно-демографическая теория описывает взаимодействие не двух, а трех сил: народа, элиты и государственного аппарата.
Цитата из интереснейшей статьи Петра Турчина:
«Структурно-демографическая теория (СДТ) представляет общество как динамическую систему, состоящую из трех основных подсистем: народ, элиты, государство [438]. Термин «элиты» используется нами в социологическом смысле: сегмент населения, который концентрирует власть в своих руках, «правящий класс». Т. к. в США основной вид социальной власти (из четырех, выделяемых Манном [439]) – экономический, то в первом (и достаточно точном) приближении мы можем определить американскую элиту как 1% наиболее состоятельных людей, которые контролируют американскую экономику (например, в 2007 г. в США этот сегмент населения владел 34, 6% всего национального достояния и 49, 7% инвестиционных активов) [440].
Нелинейные связи в системе народ – элиты – государство приводят к долгосрочным колебаниям в демографических, экономических, социальных и политических структурах обществ, «вековым циклам». Вековой цикл состоит из двух фаз: интегративной (сильное государство, внутренний мир и порядок) и дезинтегративной (слабое государство, социальная и политическая нестабильность, революции и гражданские войны). Характерная продолжительность каждой фазы – около столетия.
Переход от интегративной фазы к дезинтегративной происходит в результате действия трех основных структурно-демографических процессов, рассмотренных ниже. Заметим, что некоторые из этих процессов уже были изучены Томасом Мальтусом, другие – Карлом Марксом, третьи – Максом Вебером. Однако СДТ не является ни грубой мальтузианской теорией, ни неомарксизмом, а скорее новой синтетической теорией». [441]
Комментарий.
В стационарной, стабильной ситуации (в период, названный в статье интегративной фазой цикла) элиты и государственный аппарат представляют собой противостоящее Народу единое целое. Лишь в завершающей, дезинтегративной фазе цикла, когда перепроизводство элит приводит к появлению в ней страты «контрэлиты», слоя оттесненных от «корыта» недовольных, можно говорить о существовании в социуме трех взаимодействующих сил.
С триадной точки зрения на дезинтегративной фазе цикла происходит перепроизводство не элиты, а Дельцов в элите. Дельцы начинают активно делить «корыто» – что заканчивается революцией (к власти в стране приходят Воины из своих) или завоеванием страны соседним государством (к власти в стране приходят Воины чужие, из-за рубежа).
В подтверждение сказанному еще одна цитата из упомянутой статьи Петра Турчина: «В отличие от марксизма, согласно которому государство – не более чем орудие в руках правящего класса, в СДТ государство и элиты представляются как автономные подсистемы, хотя степень автономности может изменяться очень существенно. Например, в республиканском Риме элиты (сенаторский класс) и государство (сенат) были практически тождественны. С другой стороны, в таких бюрократических империях, как многие китайские, государство обладало высокой степенью автономности. В США XIX в. государство почти соответствовало марксистской модели. Однако в результате реформ, проведенных во время двух мировых войн (и во время Великой депрессии), оно перераспределило значительную часть ресурсов в свою пользу и получило бó льшую степень автономности (которую, впрочем, не следует переоценивать). Именно в это время доля ВНП, идущая на государственные нужды, выросла с 2% до 20%. Поэтому динамика государства играла незначительную роль в дезинтегративных процессах первого векового цикла США, но в XXI в., скорее всего, ситуация будет обратной».
Прежде чем перейти к «конструированию» системы дифференциальных уравнений, моделирующих движение триадной системы, сошлюсь на примеры подобной системы, существующие в живой природе.
На работу Алексея Меркурьевича Гилярова (1943–2013) – советского, русского зоолога, эколога, гидробиолога, публициста, доктора биологических наук, в которой описана возможность сосуществования трех колоний микроорганизмов: «Межвидовые отношения, построенные по принципу игры «камень–ножницы–бумага» (каждый вид контролирует рост численности какого-то другого вида, но сам при этом находится под контролем третьего), по-видимому, действительно встречаются в природе. Математическая модель становления сообщества разных видов, связанных подобным образом, показывает, что при размножении видов и расселении их по поверхности субстрата формируется сложная пространственная структура – чередование участков, занятых разными видами. (...)
В одной из математических моделей (Czá rá n et al., 2002)[442], построенных по принципу «камень–ножницы–бумага», рассматривается популяция бактерий, в которой появляется штамм «киллера». «Киллер» вырабатывает токсин, с помощью которого он уничтожает конкурентов и высвобождает пространство для роста собственных колоний. Однако, согласно модели, через некоторое время в популяции появляется «резистентный» штамм, устойчивый к действию токсина «киллера». Кроме того, в среде (точнее, в модели) продолжает существовать исходный «чувствительный» штамм. Выживание последнего обеспечивается очень высокой скоростью его размножения – ведь ему не надо расходовать ресурсы ни на производство токсина, ни на средства его нейтрализации. Скорость размножения «киллера», наоборот, наиболее низкая из всех трех штаммов (из-за трат на токсин и на защиту от него собственного организма). Скорость размножения «резистентного» штамма – промежуточная между «киллером» и «чувствительным»: он несет расходы на выработку противоядия, но не на сам токсин. Математическая модель такого сообщества из трех штаммов (видов), растущих на поверхности питательного субстрата и фактически конкурирующих за пространство обитания, показывает, что устойчивое сосуществование видов со временем достигается. При этом участки, занятые разными видами, образуют своего рода чересполосицу».[443]
В работе[444] Ivan D.Chase описывает случаи возникновения нетранзитивных триадных отношений лидерства-подчинения (так называемые «pecking triangles»), складывавашихся в группах домашних кур.
В статье Александра Маркова «Внутригрупповое сотрудничество помогает бактериальным популяциям противостоять конкурентам»[445] показано, что популяция, в рамках которой три вида бактерий взаимодействуют друг с другом триадным способом, по схеме «камень–ножницы–бумага», обладает преимуществом в борьбе за выживание с внешними бактериальными колониями. Так результаты научных исследований, изучающих взаимодействия колоний бактерий, подкрепляют нашу мысль о необходимости построения в России триадной системы управления, которая позволит стране получить конкурентные преимущества перед внешними цивилизационными конкурентами.
Заметка на полях.
Мысль о том, что социальные и природные системы существуют по одним и тем же законам, довольно популярна: в одной из своих книг писатель Сергей Норка, в недавнем прошлом кадровый офицер ГРУ, пишет:
«Термин «экология» означает равновесие в любой макро- или микросистеме, то есть наличие в системе составляющих ее элементов именно в той пропорции, которая является необходимым фактором для нормального функционирования, а иногда и существования самой системы. Если мы рассматриваем окружающую среду, то есть макросистему, то для нормального функционирования всех входящих в ее структуру биосистем необходима правильная пропорция всех имеющихся в этой макросистеме биологических и химических элементов.
Если вдруг под воздействием каких-либо факторов в природе, скажем, уменьшается количество кислорода или увеличивается количество углеродных соединений или тяжелых металлов, то данное нарушение экологии, то есть нарушение равновесия между всеми химическими элементами, вызывает различные, часто необратимые процессы, которые ставят под угрозу существование различных биологических элементов макросистемы и иногда саму макросистему. Это может вести к мутации или исчезновению целых видов фауны и флоры.
Природа старается регулировать все. Скажем, если в какой-то местности появляется избыток лосей, угрожающих местной флоре, то природа направляет туда «чистильщиков» – волков. Волки – это великие блюстители биологического равновесия. Когда-нибудь прозревшее человечество поставит памятник неизвестному волку, как ставило неизвестному солдату.
Так вот. Человеческое общество – это примитивная биологическая система, которая, как и любая другая система, имеет свои экологические показатели. Маркс был первым социальным экологом, разбившим общество на виды. Но эта разбивка была слишком примитивна, чтобы показать всю социальную экологию. Маркузе пошел дальше. Он разбил классы на страты, чем указал на наличие ряда социальных элементов, упущенных Марксом. Соотношение этих элементов и есть социальная экология. Ее нарушение ведет к различным негативным социально-экономическим процессам. Каким образом человек оказывается в той или иной социальной группе? На 95% это обусловлено его генетическими составляющими, конечным продуктом которых является его социальное поведение и его социальные возможности. В обществе не может быть двух одинаковых, а следовательно, двух равных людей. В любом обществе существует психологический тип людей, представляющих угрозу этому обществу. И состояние общества зависит от соотношения опасных и безопасных для него людей. Если количество опасных превышает норму, то это нарушение социальной экологии.
Должен сказать, что советская система пыталась отнестись к преступникам как к психологическому типу и наивно пыталась изменить его опасную для общества психологию путем перевоспитания, забывая при этом изменить его генетический код. С таким же успехом они могли перевоспитывать слепых и хромых от рождения». [446]
Приступая к описанию дифференциальных уравнений, описывающих движение триадной системы, еще раз с благодарностью вспоминаю работы[447] Владимира Баранова, подсказавшие мне возможность применения модели «жертва–хищник–суперхищник» к описанию цикличной триадной динамики.
Напишем уравнение для популяционной динамики, введя нового участника, суперхищника Z, являющегося жертвой членов популяции X и хищником для членов популяции Y.
Новое, третье уравнение в своей левой части будет содержать производную dZ/dt, в правой части будут присутствовать как члены, отвечающие за динамику популяции Z в качестве жертвы популяции X, так и члены, отвечающие за динамику популяции Z в роли хищника для популяции Y. В результате получаем:
dZ/dt = h * Z * Y – i * Z * X – j * Z, [3]
где h, i, j > 0.
Обратите внимание, мы считаем, что члены популяции Z питаются исключительно членами популяции Y (положительный знак перед членом «h * Z * Y» означает, что после встречи Z с Y число Z увеличивается), при этом сами члены популяции Z (и только они) являются пищей для членов популяции X (отрицательный знак перед членом «i * Z * X» – после встречи Z с X число Z уменьшается). Третий член в правой части уравнения отражает ту простую мысль, что в отсутствие пищи, коей для членов популяции Z являются члены популяции Y, популяция Z вымирает, даже в отсутствие питающихся ею членов популяции X, – вымирает по естественным причинам (от голода и по старости). В СДУ Лотки–Вольтерры [1] в правой части первого уравнения коэффициент при Х имеет положительный знак, что указывает на наличие ресурса, питания для карасей – для жертвы в этой простой модели «жертва–хищник». В нашем же случае система замкнута, и три участника модели питаются исключительно друг другом.
Модифицировав аналогичным способом первые два уравнения модели Лотки–Вольтерры [1], получим систему уравнений для нашей циклически замкнутой модели «жертва–хищник–суперхищник–жертва»:
dX/dt = a * X * Z – b * X * Y – c * X,
dY/dt = e * Y * X – f * Y * Z – g * Y,
dZ/dt = h * Z * Y – i * Z * X – j * Z, [4]
где dX/dt, dY/dt, dZ/dt – соответственно производные от X, Y и Z по времени;
X – число жертв;
Y – число хищников;
Z – число суперхищников (в свою очередь являющихся жертвами X);
a, b, c, e, f, g, h, i, j > 0.
Заметка на полях.
Вот он, записанный на языке математики принцип гармоничного существования общества, скрепляющий в единое целое представителей трех разных социотипов. Важность приведенной СДУ трудно переоценить – не удивлюсь, если придет время, когда она будет золотыми нитками вышита на треугольном знамени построенной на триадном принципе грядущей страны ГАМАЮН.
Физический (вернее, биологический) смысл у приведенной модели появляется, если популяции карасей и щук дополнить популяцией червей, питающихся исключительно щуками (черви, таким образом, выступают в качестве суперхищника). Сами щуки при этом червей не едят, зато караси червей поедают с превеликим удовольствием (аналогия довольно натянутая – в живой природе щуки довольно редко становятся жертвами червей). Впрочем, и формирующие социальную триаду Воины, Дельцы и Жрецы, чье взаимодействие мы стремимся описать приведенной системой уравнений, также практикуют каннибализм лишь в исключительно неблагоприятных жизненных условиях.
Аналогично решению двумерной системы уравнений (см. рис. 19б), одним из решений СДУ [4] является периодическое колебание, показанное на рис. 21.
Соответствующий системе уравнений [4] орграф приведен на рис. 22.

Рис. 21. Вариант решения СДУ «жертва–хищник–суперхищник» – периодические колебания

Рис. 22. Схема СДУ «жертва–хищник–суперхищник» – периодические колебания
Как и прежде (см. рис. 17), параметры модели, обозначенные на рис. 22 литерами a, b, e, f, h, i, есть коэффициенты, описывающие интенсивность взаимодействия между собой жертв (X), хищников (Y) и суперхищников (Z). Нетрудно заметить, что, в отличие от представленной на рис. 17 схемы взаимодействия, наша абсолютно симметрична относительно трех взаимодействующих элементов.