III шаг

Основные переменные: x , x , x , x .

Неосновные переменные: x , x .

Выражаем основные переменные через неосновные, начиная с разрешающего уравнения (из него выражается x ). Песле преобразований получаем

x = 3 - x + 3 x ,

x = 5 - x , (6)

x = 5 + 2 x - 5 x ,

x = 12 + 3 x - 9 x

Базисное решение Х 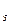= (3; 5; 0; 5; 0; 12) соответствует вершине В (3; 5;). Выражаем целевую функцию через неосновные переменные: F = 2 x + 3 x = 2(3 - x + 3 x ) + 3(5 - x ) = 21 - 2 x + 3 x . Третье базисное решение тоже не является оптимальным, т.к. при переменной x в выражении целевой функции через неосновные переменные содержится положительный коэффициент. Переводим x в основную переменную. При определении наибольшего возможного значения x обратим внимание на первое уравнение системы (6), которое не накладывает ограничений на значение переменной. При любом неотрицательном значении x переменная x будет неотрицательна. Поэтому x = min(; 5; 1; 12/9) = 1. Третье уравнение является разрешающим, а переменная x переходит в неосновные.

IV шаг

Основные переменные: x , x , x , x .

Неосновные переменные: x , x .

После преобразований получим

x = 6 + x - x ,

x = 4 - x + x ,

x = 1 + x - x ,

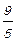x = 3 - x + x .

Базисное решение Х = (6; 4; 0; 0; 1; 3) соответствует вершине С(6; 4). Целевая функция, выраженная через неосновные переменные, имеет вид: F = 24 - x - x . Это выражение не содержит положительных коэффициентов при неосновных переменных, поэтому значение F = F(Х ) = 24 максимально.

Полученное решение является оптимальным решением задачи. Оно показывает, что максимальная прибыль, полученная от реализации произведенной продукции, составляет 24 денежные единицы, объем продукции 1-го вида – 6 единиц, продукции 2-го вида – 4 единицы. Дополнительные переменные x , x , x , x показывают разницу между запасами ресурсов каждого вида и их потреблением, т.е. остатки ресурсов. При оптимальном плане производства x = x = 0, т.е. ресурсы первого и второго видов израсходованы полностью, а ресурсы третьего и четвертого видов имеют остатки, равные соответственно 1 и 3 единицам.

Приведенное решение позволяет сформулировать критерий оптимальности решения при отыскании максимума целевой функции: если в выражении целевой функции через неоновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то решение оптимально.