Оптимизационные задачи. Содержательная и математическая постановка

Проблема эффективности является центральной в управлении большими (сложными) системами. Целью управления в конечном итоге является достижение высокой эффективности функционирования сложной экономической системы.

Под эффективностью понимают характеристику, которая отражает приспособленность системы к выполнению свойственных ей задач.

Оценку эффективности производят, как правило, математическими методами, которые позволяют получить количественное выражение данной характеристики системы. Естественно, что используемые при этом понятия также должны быть представлены количественно, или как говорят - квантифицированы. Для этого были введены понятия «показатель» и «критерий» эффективности.

Под показателем понимают количественное выражение какого-либо свойства системы или процесса. Например, важнейшим свойством сложной технической системы является ее надежность. В качестве показателя надежности принимают вероятность того, что система будет правильно функционировать в требуемых условиях дольше, чем некоторое заданное время.

С понятием эффективности органически связана проблема оптимизации, заключающаяся в том, чтобы выбрать одно из альтернативных решений, а именно то, которое является наилучшим в некотором смысле, или, как говорят, оптимальное решение.

Если мы ставим в соответствие цели некоторый численный показатель (например, надежности - вероятность), то он и будет измерителем эффективности. Граничное же значение показателя, отвечающее достижению цели, будет критерием эффективности.

Выбор критерия эффективности имеет решающее значение для принятия правильного решения и является одним из самых ответственных этапов организационного менеджмента и исследования операций.

При математической формализации цель функционирования организации представляется через количественный показатель в виде функции, называемой целевой функцией. Экстремум данной функции, который подлежит найти на области ограничений, отвечающих реальным ресурсным возможностям организации, и будет критерием ее эффективности.

Ресурсные возможности выражают через переменные, входящие в целевую функцию, и ограничения на них.

Набор переменных, при котором целевая функция достигает экстремума, представляет собой оптимальное решение и доставляет максимальную эффективность организации.

Максимальная эффективность в зависимости от конкретных условий может означать:

· получение максимального эффекта (результата) при заданных затратах;

· достижение заданного эффекта при минимальных затратах;

· максимальное отношение результата к затратам, т.е. максимальный эффект на единицу затрат.

Задача оптимизации точно может быть решена математически только для одного критерия оптимальности.

В общем случае применяются следующие способы выделения критерия оптимальности при наличии нескольких целевых показателей:

· часть показателей превращают в ограничения;

· несколько показателей свертывают (объединяют) в один обобщенный показатель (путем постановки общей цели, введением весовых коэффициентов и др.;

· варьируют постановку задачи, т.е. производят оптимизацию при разных критериях оптимальности и решение принимают на основании компромисса (метод уступок).

Пример формализации. (Определение оптимального плана выпуска продукции).

Имеется 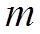видов ресурсов в количестве, определяемом вектором 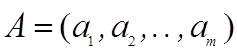, которые могут использоваться для производства 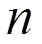видов продукции. Норма расхода 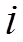- го ресурса на производство одной единицы -й продукции определяется величиной 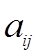, 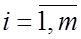; 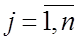. Эффективность выпуска единицы 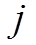-й продукции характеризуется показателем удельного дохода , .

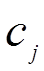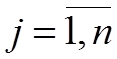Цель моделирования состоит в том, чтобы определить такой план выпуска продукции (расхода ресурсов), при котором общий эффект (суммарный доход) от проведения данной операции окажется максимальным.

Построим математическую модель процесса.

Планируемый выпуск продукции обозначим через , .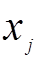

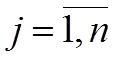Целевая функция в этом случае может быть записана в виде

.

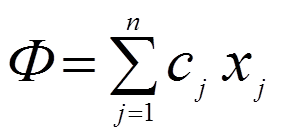Учитывая имеющееся количество ресурсов, запишем ограничения, которые определяют допустимую область решений:

, .

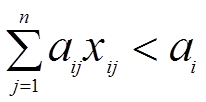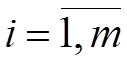Задача такого исследования состоит в поиске неотрицательных значений переменных 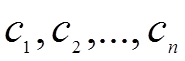, которые удовлетворяют ограничениям и обращают в максимум критерий эффективности.