Либо по другому.

На прямой возьмем текущую точку . Образуем вектор . Этот вектор должен быть перпендикулярен прямой или параллелен ее нормальному вектору . Их скалярное произведение будет равно:

Отсюда:

Так как уравнение прямой имеет вид , а точка лежит на прямой, т.е. ее координаты должны удовлетворять уравнению прямой.

Пример 11. Найти уравнение плоскости , проходящей через прямые

: и : .

Решение.

На искомой плоскости возьмем текущую точку и соединим ее с некоторой точкой прямой , координаты которой содержатся в каноническом уравнении этой прямой. Образуем текущий вектор . Из уравнений прямых получим направляющие вектора , , которые принадлежат плоскости . Заметим, что значит в составлении уравнения искомой плоскости может участвовать только один из этих векторов, например, . Отсюда возникает необходимость в том, чтобы найти еще один вектор, принадлежащий плоскости и не параллельный . Для этого на прямой возьмем некоторую точку . Координаты этой точки получим из уравнения прямой . Имеем . Составим вектор .

Для любой точки условие дает уравнение искомой плоскости α:

Пример 12. Найти уравнение плоскости , проходящей через точку 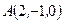, перпендикулярно прямой :

.

Решение.

На искомой плоскости составим текущий вектор . Найдем направляющий вектор :

= .

Для любой точки вектора и перпендикулярны, следовательно, для них выполняется условие , которое дает уравнение плоскости :

.

Пример 13. Найти уравнение прямой , проходящей через точку , перпендикулярно плоскости : .

Решение.

На прямой образуем текущий вектор .

Из общего уравнения плоскости получим координаты ее вектора нормали .

Так как для любой точки вектора , то условие коллинеарности

представляет собой уравнение искомой прямой.

Пример 14. Найти уравнение плоскости , проходящей через прямую :

перпендикулярно плоскости :

.

Решение.

На плоскости произвольным образом отметим точку . Каноническое уравнение прямой содержит координаты некоторой точки , лежащей на этой прямой. Соединив точки и , образуем текущий вектор .

Из уравнения прямой найдем направляющий вектор . Так как , , то . Из общего уравнения плоскости найдем координаты вектора нормали . Поскольку , , то .

Для любой точки вектора , , компланарны. Так как не параллелен , то условие порождает уравнение плоскости:

Пример 15. Дана прямая :

и плоскость :

.

a. Проверить, являются ли и параллельными.

b. Проверить, являются ли и перпендикулярными.

c. Найти угол между и .

Решение.

a) Из заданных уравнений получим координаты направляющего вектора прямой и вектора нормали плоскости.

Если , то . В нашем случае условие перпендикулярности векторов не выполняется, так как . Стало быть, не параллельна .

b) Если , то . В нашем случае условие параллельности векторов не выполняется, так как

.

Следовательно, не перпендикулярна .

d. Угол между прямой и плоскостью вычислим по формуле:

.

Отсюда .

Пример 16. Найти точку пересечения прямой

и плоскости

.

Решение.

Параметрическое уравнение прямой имеет вид:

.

Подставим эти значения в уравнение плоскости:

,

получим . Откуда . Следовательно, точка пересечения имеет координаты .

Пример 17. Найти полярные координаты точки . Решение. r= , , , . Так как угол находится в четверти, то . Отсюда, , или .

Пример 19. Установить, что уравнение

определяет гиперболу. Найти ее центр , полуоси, координаты фокусов , , вершины , , эксцентриситет, уравнения директрис и асимптот. Сделать чертеж.

Решение: 1. В уравнении линии выделим полные квадраты при одноименных переменных:

.

Разделив обе части уравнения на , будем иметь:

.

2. Введем новую систему координат 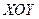, полученную сдвигом по каждой из координатных осей и связанную с равенствами:

(2).

В этой системе исследуемое уравнение представляет собой каноническое уравнение гиперболы:

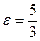с центром в точке , вещественной полуосью и мнимой . Точки , , где являются фокусами гиперболы, отсюда находим , , . Эксцентриситет , в нашем случае . Вершины гиперболы располагаются по оси симметрично относительно начала координат и на расстоянии от центра, поэтому , . По формулам асимптот и директрис:

и , найдем

- уравнения асимптот, - уравнения директрис.

3. Вернемся к исходной системе координат , воспользовавшись равенствами (2):

, , ,

, .

Асимптоты: ,

Директрисы: .

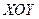4. Теперь построим гиперболу. С помощью параллельного переноса системы координат образуем новую систему координат так, чтобы новое начало координат совпадало с точкой . При указанном выборе, оси координат системы 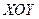являются осями симметрии гиперболы, а точка - центром симметрии.

Теперь симметрично по оси отложим отрезки длины , а по оси отрезки длины , образуем основной прямоугольник гиперболы. При пересечении основного прямоугольника с осью образуются вершины , . Через противоположные вершины основного прямоугольника проведем прямые, которые будут являться асимптотами гиперболы. Теперь проводя через вершины и приближаясь к асимптотам, рисуем ветви гиперболы. Фокусы гиперболы и располагаются по оси абсцисс симметрично начала координат на расстоянии .

Пример 20. Установить, что уравнение 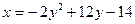определяет параболу, найти ее вершину, параметр, фокус, директрису. Сделать чертеж.

Решение: 1. В заданном уравнении сгруппируем слагаемые, содержащие переменную y, вынесем коэффициент при квадрате за скобку и выделим полный квадрат:

.

2. Введем новую систему координат 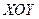, связанную со старой, следующими формулами:

, (3)

тогда исследуемое уравнение относительно новых осей примет вид:

.

Полученное уравнение представляет собой каноническую форму уравнения параболы, симметричной относительно оси , с ветвями, направленными в отрицательную сторону , и вершиной в точке . Константа перед , есть величина , поэтому , а параметр .

Фокус и уравнение директрисы при таком расположении параболы находятся по формулам , , отсюда имеем фокус , директриса .

3. Вернемся к исходной системе координат . Используя равенства (3), получаем: , , директриса .

4. Построение параболы. С помощью параллельного переноса системы координат так, чтобы новое начало координат совпадало с точкой , образуем новую систему .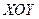

Рисуем параболу с вершиной в точке и обладающую перечисленными выше свойствами.

Фокус параболы лежит на расстоянии от вершины. Директриса параболы проходит через точку параллельно .