Прямая многократная засечка. Постановка задачи. По левые работы.

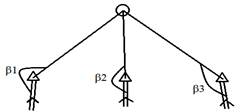
Выполняется при наличии 3-ех исходных пунктов и 3-ех исходных сторон.

r = 3 - 2 = 1

x = x_p + δ _x

y = y_p + δ _y

δ _x и δ _y - поправки в приближенные значения.

m_β = √ ∑ PVV/(n-k) - оценка точности полевых измерений

где V = V_{β i} – поправка в измеренные углы

Р – вес результата измерений

Мр = √ m²_x + m²_y

m_x = m_β /√ P_x

m_y = m_β /√ P_y

По заданной Мр не выполняя полевых измерений можно предрасчитать точность, выбрать средства измерений и разработать методику.

Обратная однократная засечка. Вывод формул вычисления координат пункта.

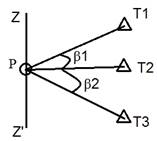
Дано:

x_T1, y_T1

x_T2, y_T2

x_T3, y_T3

Найти:

x_p и y_p

Пункт P закреплен таким образом, чтобы была видимость. Способом круговых приемов измеряются горизонтальные углы. На пункте Р устанавливается прибор.

Обратная геодезическая задача

(y_T1 – y_p) = (x_T1 – x_p)tgα ₁

(y_T2 – y_p) = (x_T2 – x_p)tgα ₂

(y_T3 – y_p) = (x_T3 – x_p)tgα ₃

α, x, y – неизвестные.

Раскрывая функцию tg как суммы 2-ух углов и выражая искомое неизвестное получаем:

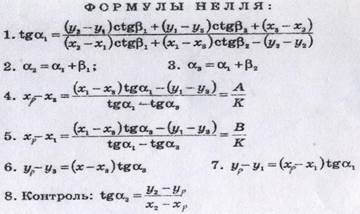
Обратная однократная засечка. Оценка точности планового положения пункта.

Единственный контроль – графическое определение координат пункта Р.

М²р = 1/4F² * (Ϭ ₁² + Ϭ ₂² + Ϭ ₃²)*m²_u

Путем построения инвертного треугольника.

F – площадь треугольника.

Ϭ _i – стороны треугольника.

m_u – СКО измерения 1-ого направления.

Направление – угол, образованный нулевым диаметром лимба и следом коллимационной плоскости, образованном при визировании на цель.

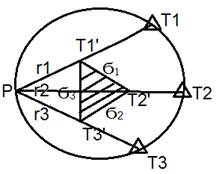
Опасный круг

PT2 = D

ri = ρ /Si – градиент направления

а = ρ /D

В этой ситуации площадь инвертного треугольника будет равна 0, а Мр стремится к бесконечности. Это означает, что при расположении пунктов на 1-ой окружности, задача не имеет решения. Чтобы не попасть в этот «опасный» круг, самое лучшее положение пункта Р внутри этой окружности.