Схема и модель МОБ производства и распределения продукции

Введем необходимые для дальнейшего понятия.

Промежуточным продуктом (промежуточным спросом ) будем называтьчасть валового продукта (спроса), представляющего собой закупки i-го вида продукции j-ми отраслями в качестве исходных материалов, т.е. это продукт, который поступает из i-й отрасли в j-ю для дальнейшей переработки в текущем периоде. В дальнейшем будем обозначать его через x_ij.

Напротив, конечным продуктом (конечным спросом) будем называть часть общего спроса, представляющего закупки конечных продуктов, т.е. продуктов, выходящих из сферы производства в область конечного использования на потребление и инвестиции. Конечный продукт превышает объем национального дохода, используемого на потребление и накопление на величину возмещения выбытия основных фондов и экспортно-импортного сальдо. Будем обозначать его через y_i.

Условно-чистая продукция или добавленная стоимость представляет факторные затраты отрасли, т.е. вновь созданную стоимость, распадающуюся на заработную плату, предпринимательский доход, различного вида налоги и амортизацию. Условно-чистая продукция – это стоимостной эквивалент конечной продукции, она превышает объем национального дохода на величину амортизационных отчислений. В дальнейшем будем обозначать ее через z_j.

С теоретической точки зрения МОБ представляет собой экономико-математическую модель процесса воспроизводства, которая в развернутом виде отражает взаимосвязи по производству, распределению, потреблению и накоплению каждого вида продукции в единстве материально-вещественного и стоимостного аспектов воспроизводства.

Объединение указанных характеристик в рамках единой модели на практике достигается посредством крестообразного наложения двух таблиц одна на другую. В первой из них (вертикальной) в отраслевом разрезе представлена структура затрат или структура используемых ресурсов, необходимых для каждой отрасли. В том числе и элементы условно-чистой продукции (добавленной стоимости). Во второй (горизонтальной) отражено распределение каждого вида продукции на нужды промежуточного (текущего производственного) и конечного использования. Итак, затраты отражены по столбцам таблицы, а распределение – по строкам.

Пересекающаяся часть этих двух таблиц образует так называемую “шахматку”, или первый квадрант общей схемы МОБ. Строки и столбцы “шахматки”, имеющие одинаковые номера, характеризуют процесс производства (по столбцам) и распределения (по строкам) продукции одной и той же отрасли на нужды текущего производственного потребления. Итак, в пределах “шахматки” (I квадранта МОБа) отражается внутрипроизводственный оборот (промежуточные затраты – промежуточный выпуск) предметов труда и услуг.

Межотраслевой анализ базируется на использовании статистических таблиц, называемых межотраслевыми, дающих картину общих межотраслевых пропорций за определенный период времени (как правило, за год), содержание которых составляют связи между отраслями. Рассмотрим общую схему МОБ, которая в стоимостном исчислении состоит из четырех разделов (квадрантов) (табл. 1.1.1).

Таблица 1.1.1

Общая схема межотраслевого баланса

Распределение Зат- продук- раты ции на производ- ство	Текущее производственное потребление в отраслях   1 2 … j …. n Итого	Конеч-ный продукт	Вало-вый про-дукт
Матери-   альные   затраты	… i … n	x11 x12 … x1j … x1n x21 x22 … x2j … x2n …….……I……………. xi1 xi2 … xij … xin ……………………….. xn1 xn2 … xnj … xnn		y1 y2 II… yi … yn	x1 x2 … xi … xn
	Итого	.
Условно-чистая продукция	Z1 Z2 … Zj III… Zn		IV
Валовая продукция	x1 x2 …. xj … xn

В I и II квадрантах отражаются важнейшие материально-вещественные взаимосвязи и пропорции национальной экономики, выраженные в стоимостных измерителях–отраслевая и материально-вещественная структура фондов текущего производственного потребления и конечной продукции.

Каждая строка таблицы характеризуется следующим балансом:

Выпуск данного вида продукции = Промежуточный спрос + Конечный спрос,

или , (1.1)

где x_i – валовой продукт i-й отрасли;

n - число отраслей.

В I и III квадрантах находят отражение важнейшие стоимостные пропорции по производству национального продукта. Здесь отражена стоимостная отраслевая структура затрат или структура используемых ресурсов, необходимых для каждой отрасли.

Каждый столбец таблицы характеризуется следующим балансом:

Расходы отрасли = Промежуточные затраты + добавленная стоимость,

что в математической записи выглядит так:

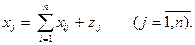(1.2)

Единство материально-вещественного и стоимостного составов валового (совокупного) национального продукта, конечного продукта и национального дохода проявляется в сбалансированности итогов строк и столбцов МОБ: итоги одноименных строк и столбцов таблицы МОБ равны, т.е. равны выпуск и расходы отрасли:

(при i = j),

а следовательно, общая сумма конечного спроса равна общей сумме добавленной стоимости:

. (1.3)

Равенство (1.1) называется системой уравнений распределения продукции, равенство (1.2) – системой уравнений производства продукции, а (1.3) – основное балансовое соотношение.

Будем считать, что объемы промежуточного производственного потребления прямо пропорциональны объемам производства продукции потребляющих отраслей, т. е.

x_ij = a_ij x_j (i, j = ), (1.4)

где коэффициентами пропорциональности a_ij являются коэффициенты прямых материальных затрат, определяемые из соотношений:

a_ij = x_ij / x_j (i, j = ). (1.5)

Из (1.5) следует смысл этих коэффициентов; они показывают объем материальных ресурсов i-го вида, необходимый для производства единицы валового продукта j-го вида. После подстановки (1.4) в (1.1) получаем

. (1.6)

Это и есть система уравнений модели В. Леонтьева “затраты-выпуск”, называемая статической моделью МОБ. Рассчитаем равновесный выпуск, найдя решение системы линейных уравнений (1.6), т.е. x_i (i = ) при фиксированных значениях спроса на конечную продукцию y_i (i = ).

Запишем систему уравнений (1.6) в матричной форме:

X = AX + Y, (1.6а)

(1.6а) является моделью МОБ леонтьевского типа.