Расчет равновесного выпуска и равновесных цен

Решим уравнение (1.6а) относительно Х, определив равновесный выпуск отраслей, обеспечивающий заданный уровень спроса Y на конечную продукцию. Известно, что

X = (E – A)^-1 Y. (1.7)

Матрица

В = (Е – А) ^–1 (1.8)

называется обратной матрицей Леонтьева или матричным мультипликатором, или мультипликатором Леонтьева. Ее элементы (b_ij) показывают потребность в валовом выпуске продукции i-й отрасли для производства единицы конечной продукции j-й отрасли. Матрица В является мультипликатором, отражающим эффект распространения спроса на валовую продукцию, первоначальным источником которого является спрос на конечную продукцию. Перепишем (1, 7) с учетом (1, 8) в виде

X = (1.9)

Элементы матрицы В называются коэффициентами полных материальных затрат. С учетом линейности соотношений (1.9) эффект распространения спроса DX, вызванный изменением конечного спроса на величину DY рассчитывается как

DX =

Говорят, что решение системы уравнений МОБ позволяет определить равновесный выпуск, имея в виду под общим равновесием соотношение в экономической системе, которое характеризуется равновесием спроса и предложения всех ее ресурсов.

Определим равновесные цены, воспользовавшись системой уравнений производства продукции. Равновесные цены позволяют исследовать эффект распространения изменения цены, вызванный изменением элементов добавленной стоимости и построить ценовую модель МОБ.

Введем в рассмотрение v_j = z_j/x_j - величину добавленной стоимости, приходящейся на единицу валовой продукции отрасли, называемой долей добавленной стоимости. Тогда, учитывая, что z_j = v_j x_j, (1.2) перепишем в виде:

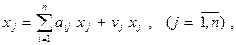(1.10)

или

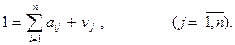(1.11)

Это выражение описывает формирование цены каждого вида продукции в базовом периоде, если ее принять за единицу. Слагаемое показывает возмещение стоимости, а v_j – вновь созданную стоимость

(с учетом амортизации и налогов). Система равенств (1.11) представляет собой модель балансовых цен, на основе которой можно выяснить, как через посредством структуры потребляемых каждой отраслью ресурсов изменяется структура цен при варьировании величины добавленной стоимости.

Если для расчетного периода доля добавленной стоимости будет равна v_j, то цены P_j (j = ) будут определяться по (1.11) из соотношений

(1.12)

В матричном виде эту систему можно переписать как

, (1.13)

где

А^т – обозначает матрицу, транспонированную к матрице А.

Решим (1.13) относительно Р. Получим

(1.14)

Уравнения (1.12) и (1.13) называют моделью равновесных цен, а матрицу В^т – ценовым матричным мультипликатором (матричным мультипликатором ценового эффекта распространения).

Эффект распространения DР, вызванный изменением доли добавленной стоимости на DV может быть рассчитан из (1.14) как

D .