
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Деформація кручення та деформація згину
|
|
Крученням називається такий вид деформації, при якому в поперечних перерізах стержня виникає тільки один внутрішній силовий фактор – крутний момент Мк. Крутний момент позначається також Мх, оскільки це момент внутрішніх сил відносно повздовжньої осі стержні – осі х. Кручення виникає у валах, гвинтових пружинах та інших елементах конструкції.
Кручення прямого стержня відбувається при навантаженні його зовнішніми скручуючими моментами (парами сил), які діють у площинах перпендикулярних до осі стержня. При розрахунках валів величини зовнішніх скручуючих моментів (в основному) визначаються за величиною потужності яка передається на вал і за швидкістю обертання валу
 (1)
(1)
n – кутова швидкість, об/хв.;
N – потужність, Вт;
m – момент, Н× м.
Отже для визначення величини крутних моментів у перерізі валу слід знати величину зовнішніх скручуючих моментів. Крутні моменти, які виникають у поперечних перерізах стержнів, визначають за зовнішніми скручуючими моментами методом перерізів.
Крутний момент в довільному поперечному перерізі стержня чисельно дорівнює алгебраїчній сумі зовнішніх скручуючих моментів, прикладених до стержня по один бік від розглянутого перерізу.
При розрахунку на міцність і жорсткість знак крутного моменту не має значення, але для зручності побудови епюр Мк приймають правило знаків:
Крутний момент буде додатнім, якщо на торці відсіченої частини стержня він направлений за годинниковою стрілкою
При розрахунках стержня на кручення потрібно розв’язати дві основні задачі. Необхідно визначити напруження в поперечних перерізах стержня і знайти кутові переміщення в залежності від зовнішніх моментів. Ці задачі розв’язуються по різному, дивлячись, який вигляд має поперечний переріз.
Найбільш просто (найпростіше) можна отримати розв’язок у випадку круглого стержня, а також для широкого класу тонкостінних стержнів.
Теорія кручення стержнів круглого перерізу (або кільцевий переріз) ґрунтується на наступних положеннях.
1. поперечні перерізи стержня, залишаються плоскими і перпендикулярними до його осі, повертаються при кручені один відносно одного на певний кут, який називається кутом закручування (гіпотеза плоских перерізів (гіпотеза Бернулі).
2. радіуси поперечних перерізів не викривляються і зберігають свою довжину.
3. віддаль (вздовж осі стержня) між поперечними перерізами не змінюється.
Формули виведені на основі цих положень співпадають з формулами, одержаними точними методами (без прийняття будь яких гіпотез) в теорії пружності і пітверджуються експериментально.
Встановлено, що при крученні круглого стержня в його поперечному перерізі виникають дотичні напруження, які збільшуються від нуля в центрі перерізу до найбільш віддаленої точки від центру.
 ρ (2)
ρ (2)
За цією формулою визначається величина дотичної напруги в довільній точці поперечного перерізу при крученні круглого бруса.
З (2) випливає, що напруги в точках, близьких до осі, малі, і крутячий момент залежить, передусім, від напруг, що виникають в частинах бруса, близьких до поверхні.
При r=r
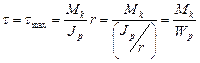 (3)
(3)
Відношення  називають полярним моментом опору перерізу.
називають полярним моментом опору перерізу.
Для круга: Wp =0, 2 d 3
де d - діаметр круга.
Для кільцевого перерізу:  (5)
(5)
де  d b, d з – внутрішній і зовнішній діаметр кільця відповідно.
d b, d з – внутрішній і зовнішній діаметр кільця відповідно.
Для повного кута закручування φ отримаємо:

 (6)
(6)
Рівняння (2.37) справедливе для ділянок з постійним Мк і постійним поперечним перерізом.
Згином називають такий вид навантаження (деформації), при якому в поперечних перерізах стержня виникають згинальні моменти. На відміну від деформації розтягу і кручення прямих стержнів, в яких прямі вісі до деформації залишаються прямими після деформації, при згині прямі вісі стержнів після деформації вигинаються, а вісі кривих стержнів змінюють свою кривизну.
Зауважимо, що прямолінійний стержень, що працює на згин здебільшого у горизонтальному положенні прийнято називати балкою.
Згин пов’язаний з виникненням у поперечних перерізах стержня згинальних моментів. Згинальний момент – внутрішній силовий фактор (внутрішнє зусилля), який виникає в поперечному перерізі стержня відносно осі, яка лежить у цьому перерізі і проходить через центр його тяжіння; він діє у площині, перпендикулярній до поперечного перерізу стержня.
Якщо площина дії згинального моменту проходить через одну з головних центральних осей інерції перерізу (така площина називається головною) то згин називається прямим. Викривлення балки відбувається у головній площині, тобто у площині, що проходить через вісь балки і одну із головних центральних осей поперечного перерізу. Якщо площина дії згинального моменту в даному поперечному перерізі стержня не проходить ні через одну із головних центральних осей інерції цього перерізу, то згин називають косим згином. Якщо у поперечному перерізі стержня виникає лише згинальний момент, а поперечні і нормальні сили відсутні, то згин називається чистим прямим або чистим косим згином, відповідно, а якщо виникає крім згинального моменту поперечна сила, то згин називається поперечним.
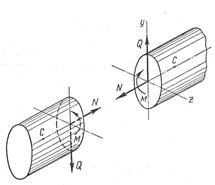
При навантаженні стержня зовнішніми силами, які діють в одній площині, що проходить через вісь стержня, то в кожному поперечному перерізі стержня можуть виникати наступні силові фактори (рис.1):
| 
|
Рис1.
а) поздовжня сила N, прикладена в центрі тяжіння перерізу перпендикулярно до перерізу;
б) поперечна сила Q, яка діє в площині поперечного перерізу і проходить через центр його тяжіння;
в) згинальний момент Мзг, що діє в площині, перпендикулярній до поперечного перерізу.
(згинальні моменти ще позначають Мz і Му, відносно осей Z iY).
Правило знаків:
Згинальний момент Мзг у поперечному перерізі вважається додатнім, якщо на лівому торці правої частини стержня він направлений за стрілкою годинника, а на правому торці лівої частини - проти стрілки годинника.
Поздовжня сила N в перерізі додатня при розтягу.
Поперечна сила Q додатня, якщо на лівому торці правої частини стержня вона направлена знизу уверх, а на правому торці лівої частини – сверху вниз. Додатня поперечна сила намагається обертати відсічену частину стержня за стрілкою годинника відносно любої точки С, розміщеній на внутрішній нормалі до поперечного перерізу.
При додатному згинальному моменті верхні поздовжні волокна балки відчувають стиск (скорочення), а нижні – розтяг (видовження).
Згинальний момент, поздовжня сила і поперечна сила, які діють у кожному поперечному перерізі пов’язана з напруженнями, які виникають у цьому перерізі наступними залежностями:
Q = ∫ τ dF (1)
F
N = ∫ σ dF (2)
F
Mz = ∫ σ y dF (3)
F
Внутрішні сили у перерізі стержня, які діють зі сторони лівої частини на праву, можна визначити за зовнішніми силами, які діють як на ліву частину, так і на праву. В цьому випадку проекції зовнішніх сил на вибрані осі і їх моменти відносно цих осей слід брати зі зворотними знаками.
Посацький, стор.140
Поперечні сили вважаються додатними, якщо вони зсовують лівий кінець елемента балки відносно правого його кінця вгору (рис. 3). Додатними вважають згинальні моменти, які згинають елементи балки опуклістю вниз.
Визначення внутрішніх сил які діють зі сторони лівої частини стержня на праву можна проводити за зовнішніми силами, прикладеними не до правої, а до лівої частини, але необхідно врахувати зворотний знак.
Це положення дозволяє сформулювати наступні правила визначення внутрішніх зусиль, які виникають у поперечних перерізах стержня, якщо всі зовнішні сили розміщені в одній площині.
1. Згинальний момент Мz відносно центральної осі Z поперечного перерізу за величиною і знаком дорівнює сумі моментів відносно цієї осі всіх зовнішніх сил, прикладених до лівої частини стержня або сумі моментів (відносно тієї ж осі) всіх зовнішніх сил, прикладених до правої частини, взятих з протилежним знаком:
Мz =  = -
= - 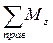 , (4)
, (4)
причому моменти зовнішніх сил приймаються додатними, якщо вони діють за
годинниковою стрілкою.
2. Поперечна сила Q за величиною і знаком дорівнює сумі проекцій всіх зовнішніх сил, прикладених до лівої частини стержня на нормаль (перпендикуляр) до його поздовжньої осі (вертикальна вісь Y у площині дії сили) або сумі проекцій (на ту ж нормаль) всіх зовнішніх сил, прикладених до правої частини балки, взятій з протилежним знаком:
Q = 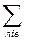 Y = -
Y = -  Y, (5)
Y, (5)
при цьому проекції зовнішніх сил на нормаль додатна, якщо вони направлені знизу у верх.
3. Поздовжня сила N за величиною і знаком дорівнює сумі проекцій всіх зовнішніх сил, прикладених до лівої частини стержня на його поздовжню вісь або сумі проекцій (на ту ж вісь) всіх зовнішніх сил, прикладених до правої частини балки, взятій з протилежним знаком:
N = 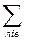 X = -
X = -  X, (6)
X, (6)
при цьому проекції зовнішніх сил на вісь стержня додатня, якщо вона
направлена справа наліво