
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценивание параметров моделей с коррелированными возмущениями
|
|
Если имеется автокорреляция возмущений, то для оценки параметров модели используют другой частный случай обобщенного метода наименьших квадратов.
Пусть по временным рядам переменных X и Y строится парная линейная модель
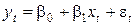 (t =1, 2, …, n), (t =1, 2, …, n),
| (33) |
уравнение регрессии которой имеет вид:
 (t =1, 2, …, n), (t =1, 2, …, n),
| (34) |
где b 0, b 1 — оценки параметров b0 и b1 соответственно.
Первоначально исходные переменные и свободный член b 0 уравнения регрессии преобразуются с помощью формул:
 ; ;
| (35) | |
 ; ;
| (36) | |
 (t =2, 3, …, n), (t =2, 3, …, n),
| (37) |
где r (1) — коэффициент автокорреляции остатков первого порядка [см. формулу (21) ].
В результате уравнение (34) трансформируется в уравнение
 (t =2, 3, …, n), (t =2, 3, …, n),
| (38) |
параметры которого определяются обычным МНК. После этого рассчитывается свободный член b 0 исходного уравнения (34) по формуле
 . .
| (39) |