N-мерное векторное пространство. Его базис

n - мерным вектором называется упорядоченная совокупность из n действительных чисел: а числа называются компонентами вектора.

n -мерный вектор можно рассматривать как матрицу с одной строкой, поэтому операции с векторами вводят аналогично матрицам:

Пусть

Под нуль-вектором понимают

Множество n -мерных векторов с введёнными операциями сложения и умножения на число называют n -мерным векторным пространством
и обозначают R_n.

Линейной комбинацией системы векторов называют выражение вида:

где — некоторые числа.

Если линейная комбинация векторов равна нуль-вектору:

(8)

и при этом коэффициенты a _i не все равны нулю одновременно, то система векторов называется линейно зависимой. Если равенство (8) возможно только тогда, когда все коэффициенты то система векторов называется линейно независимой.

Если система векторов линейно зависима, то хотя бы один из них линейно выражается через остальные.

В пространстве R_n существует система n линейно независимых векторов. Любая система из (n +1) векторов и больше линейно зависима.

Таким образом, максимальное число линейно независимых векторов в R_n равно n. Число n называют размерностью пространства R_n.

Любая система из n линейно независимых векторов в R_n называется базисом.

Теорема (критерий базиса в R_n ). Для того, чтобы система векторов образовывала базис в R_n, необходимо и достаточно чтобы определитель, составленный из координат этих векторов, был отличен от нуля.

Если система векторов образует базис в R_n, то любой вектор можно единственным образом представить в виде линейной комбинации векторов :

(9)

Формула (9) называется разложением вектора по базису а числа называются координатами вектора в этом базисе.

Приведём пример одного базиса в пространстве R_n, называемого каноническим базисом:

Пример 3. Показать, что заданная система векторов образует базис в пространстве R ₃, записать матрицу перехода от канонического базиса к базису
и разложить вектор по базису

Решение. Согласно теореме (критерий базиса в R_n), система векторов образует базис, тогда и только тогда, когда определитель, составленный из координат векторов, отличен от нуля. Вычислим этот определитель:

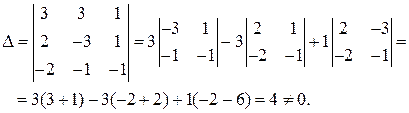
Следовательно, система векторов образует базис в пространстве R ₃. Матрица перехода от канонического базиса к базису состоит из координат векторов в базисе записанных в соответствующие столбцы, и имеет вид

Разложение вектора по базису согласно (9) ищем
в виде:

Это векторное равенство эквивалентно системе уравнений:

Поскольку определитель этой системы отличен от нуля, используем для её решения формулы Крамера:

Итак,

Сделаем проверку, подставив найденное решение в исходную систему:

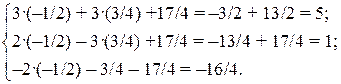
Таким образом, разложение вектора по базису имеет вид: