Решение однородных систем линейных алгебраических уравнений

Рассмотрим однородную систему уравнений:

Такая система всегда совместна, поскольку имеет нулевое решение

Однако, при определенных условиях она может иметь и ненулевое решение.

Теорема (критерий ненулевого решения однородной системы уравнений). Для того, чтобы однородная система уравнений имела ненулевое решение, необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных.

Будем рассматривать ненулевые решения системы как столбцы, состоящие из n элементов; обозначим их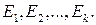

Линейно независимая система решений называется фундаментальной системой решений, если любое другое решение является линейной комбинацией решений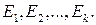

Теорема. Если ранг r матрицы системы однородных уравнений меньше числа неизвестных n, то эта система имеет фундаментальную систему решений, которая состоит из n – r линейно независимых решений исходной системы.

Общее решение однородной системы уравнений имеет вид:

(10)

где — произвольные числа.

Решение системы, полученное из общего при фиксированных значениях , называется частным.

Пример 4. 1) Считая матрицу С _{4× 5} матрицей однородной системы С·Х = 0, найти:

а) фундаментальную систему решений;

б) общее решение;

в) какое-нибудь частное решение.

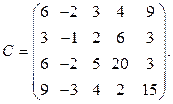
Решение. Исходная система уравнений имеет вид:

Преобразования матрицы системы оформим в виде таблицы (табл.).

С	S	Примечания
		Умножим вторую строку на –1
		Разрешающий элемент а 22=1. Разрешающую строку (вторую) оставляем без изменений. Все элементы разрешающего столбца (второго), кроме а 22, заменяем нулями. Остальные элементы преобразуем по формуле (7)
		Умножим первую строку на –1, а четвёртую строку на 1/2
		Разрешающий элемент а 13=1. Разрешающую строку (первую) оставляем без изменений. Все элементы разрешающего столбца (третьего), кроме а 13, заменяем нулями. Остальные элементы преобразуем по формуле (7)

Преобразование закончено. Получены две строки из нулей, все остальные строки преобразованы

а) Из табл. 4 следует, что ранг матрицы С равен r (C)=2, так как есть миноры второго порядка, отличные от нуля, например а любые миноры третьего и четвёртого порядков равны нулю.

Переменные системы х ₂, х ₃, соответствующие базисному минору матрицы А называются базисными переменными, остальные х ₁, х ₄, х ₅ — свободными.

Система, равносильная исходной, имеет вид:

Оставляя слева базисные переменные х ₂ и х ₃, соответствующие линейно независимым столбцам матрицы А, и перенося в правую часть уравнений неизвестные х ₁, х ₄, х ₅, получаем:

б) Полагая свободные переменные равными произвольным константам х ₁= с ₁, х ₄= с ₄, х ₅ =с ₅, получаем общее решение системы в виде:

Фундаментальную систему решений образуют три линейно независимых частных решения. Получим эти решения, задавая системе констант (с ₁, с ₄, с ₅) линейно независимые значения, например, (1; 0; 0), (0; 1; 0),
(0; 0; 1). Вычисления занесем в таблицу (табл.).

Итак, фундаментальную систему составляют три линейно независимых решения:

Общее решение однородной системы, согласно (10), имеет вид:

где с ₁, с ₂, с ₃ — произвольные константы.

в) Частное решение можно получить из общего решения, придавая определённые значения произвольным постоянным. Решения образующие фундаментальную систему решений, являются частными решениями этой однородной системы.

2) Считая матрицу С _{4× 5} расширенной матрицей неоднородной системы С ^* Х = С ^**, где С = (С ^*½ С ^**), решить эту систему, предварительно исследовав её на совместность по теореме Кронекера—Капелли.

Решение. Неоднородная система С ^* Х = С ^** имеет вид:

Чтобы исследовать систему на совместность по теореме Кронекера—Капелли, нужно проверить равенство r (С ^*)= r (С ^* С ^**). Из табл. следует,
что r (С ^*) = r (С ^* С ^**)=2, значит система совместна.

Так как ранг матрицы меньше числа неизвестных n = 4, то система является неопределенной. Множество всех решений неоднородной системы получим, решив равносильную ей систему, полученную методом Жор-дана—Гаусса:

Базисные переменные х ₂, х ₃ выразим через свободные переменные х ₁, х ₄:

Полагая свободные переменные равными произвольным постоянным х ₁= с ₁, х ₄= с ₄, находим общее решение неоднородной системы в виде:

Элементы векторной алгебры в R ₃

Трехмерное векторное пространство R ₃ есть частный случай R_n при
n = 3. Декартов прямоугольный базис в R ₃ образуют три единичных, взаимно перпендикулярных вектора

Совокупность начала координат (точки О) и декартова прямоугольного базиса называется декартовой прямоугольной системой координат Oxyz.

Согласно формуле (9) любой вектор в R ₃ можно разложить единственным образом по т. е. представить в виде:

где а_х — координата вектора по оси ОХ;

а_у — координата вектора по оси ОY;

а_z — координата вектора по оси ОZ.

Наряду с аналитическим заданием вектора как упорядоченной тройки чисел в R ₃ рассматривают вектор как направленный отрезок, имеющий начало и конец. Конец вектора отмечается стрелкой.

А — начало вектора,

В — конец вектора.

Длина отрезка АВ называется модулем вектора и обозначается или .

Если известны координаты вектора то модуль вектора вычисляется по формуле:

(10)

Радиусом-вектором точки в декартовой прямоугольной системе координат называется вектор, начало которого расположено в начале координат, а конец в данной точке А, т. е. вектор

Координатами точки А называются координаты её радиуса-вектора. Если то координаты точки А.

Пусть вектор 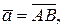причём заданы координаты точек А и В: и Тогда координаты вектора равны разности одноимённых координат конца и начала:

(11)

Из (10) и (11) следует формула для расстояния между двумя точками А и В:

(12)

Скалярным произведением векторов и называется число (скаляр), обозначаемое , равное произведению модулей векторов на косинус угла между ними:

(13)

где j — угол между векторами и .

В декартовой прямоугольной системе координат скалярное произведение векторов вычисляется по формуле:

(14)

— координаты вектора ;

— координаты вектора .

Из (13) и (14) получается формула для вычисления косинуса угла между двумя векторами:

(15)

Векторы и называются ортогональными (обозначаются если угол j между ними равен прямому, т. е. cosj = 0. Условие ортогональности векторов:

(16)

Упорядоченная тройка векторов называется правой, если
из конца третьего вектора кратчайший поворот от первого вектора
ко второму виден происходящим против часовой стрелки и называется левой, если такой поворот происходит по часовой стрелке.

Векторным произведением вектора на вектор называется вектор такой что:

1) т. е. перпендикулярен плоскости векторов и

2) направлен так, что тройка — правая;

3) модуль вектора равен площади параллелограмма, построенного на векторах и , как на сторонах, т. е.

(17)

Если то для векторного произведения справедлива формула:

(18)

Смешанным произведением упорядоченной тройки векторов называется число (обозначаемое ()), равное скалярному произведению векторного произведения первых двух векторов на третий:

Смешанное произведение векторов по абсолютной величине равно объему параллелепипеда , построенного на этих векторах как на сторонах, т. е.

(19)

Если то справедлива формула:

(20)

Векторы и называются коллинеарными, если они лежат на одной или параллельных прямых. Условие коллинеарности векторов и :

1) в векторной форме где l — скаляр;

2) в координатной форме (21)

Векторы называются компланарными, если они лежат в одной или параллельных плоскостях. Условие компланарности трёх векторов :

1) в векторной форме: где l, m — числа;

2) в координатной форме: (22)

Пример 5. Даны координаты вершин треугольной пирамиды:
А ₁ (–1, 0, 1), А ₂ (2, 3, 1), А ₃ (0, –2, 2), А ₄ (1, –1, 5).

Требуется найти:

а) длины рёбер А ₁ А ₂ и А ₁ А ₃;

б) угол между ребрами А ₁ А ₂ и А ₁ А ₃;

а) Используем формулы (11) и (12).

Определим координаты векторов:

Ребро

б) Угол между рёбрами А ₁ А ₂ и А ₁ А ₃ рассматриваем как угол между векторами и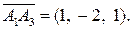

По формуле (15) для косинуса угла между двумя векторами получим:

в) Грань А ₁ А ₂ А ₃ есть треугольник, площадь которого равна половине площади параллелограмма А ₁ А ₂ А ₆ А ₃, построенного на векторах
и . По формуле (17):

Вычислим векторное произведение векторов и по формуле (18):

г) Объём треугольной пирамиды равен 1/6 объёма параллелепипеда , построенного на векторах , , как на сторонах. Из свойств смешанного произведения следует, что:

и следовательно,

Определим координаты вектора

По формуле (20) имеем

Элементы аналитической геометрии в R ₃

Направляющим вектором прямой называется любой вектор , лежащий на этой прямой или ей параллельной и отличный от нуль-вектора, т. е. и

(23)

где (x, y, z) — координаты текущей точки прямой; (x ₀, y ₀, z ₀) — координаты данной точки на прямой; (m, n, p) — координаты направляющего вектора прямой.

Если на прямой заданы две точки М ₁(x ₁, y ₁, z ₁) и М ₂(x ₂, y ₂, z ₂), то в качестве направляющего вектора прямой можно взять вектор :

Рассматривая в качестве данной точки точку М ₁ и используя уравнение (23), получим уравнение прямой, проходящей через две данные точки:

(24)

Пусть прямая l ₁ имеет направляющий вектор и прямая l ₂ — направляющий вектор .

Угол j между прямыми l ₁ и l ₂ определяется как угол между их направляющими векторами и 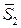, по формуле (15) получаем:

, если т. е. по условию коллинеарности (21)

Критерий перпендикулярности прямых < => Тогда по условию ортогональности векторов (16)

Нормальным вектором плоскости (П) называется любой вектор , перпендикулярный к плоскости и отличный от нуль-вектора:
и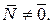

Уравнение плоскости, проходящей через данную точку М ₀ плоскости и имеющей данный нормальный вектор , имеет вид:

(25)

где А, В, С — координаты нормального вектора ;

x ₀, y ₀, z ₀ — координаты данной точки плоскости;

x, y, z — координаты текущей точки плоскости.

Если в уравнении (25) раскрыть скобки, то его можно записать в виде

(26)

Уравнение (26) называется общим уравнением плоскости.

Три точки М ₁(x ₁, y ₁, z ₁), М ₂(x ₂, y ₂, z ₂) и М ₃(x ₃, y ₃, z ₃) (не лежащие на одной прямой) определяют плос­кость в R ₃. Уравнение такой плоскости можно получить из условия компланарности (22) трёх векторов:

(27)

Здесь x, y, z — координаты текущей точки М;

x ₁, y ₁, z ₁ — координаты данной точки М ₁;

x ₂, y ₂, z ₂ — координаты данной точки М ₂;

x ₃, y ₃, z ₃ — координаты данной точки М ₃.

Пусть плоскость П задана общим уравнением

Расстояние от точки М ₀(x ₀, y ₀, z ₀)
до плоскости П вычисляется по формуле:

(28)

Угол между двумя плоскостями, нормальные векторы которых и , вычисляется по формуле:

(29)

Критерий параллельности плоскостей:

Критерий перпендикулярности плоскостей:

Пример 5. Даны координаты вершин треугольной пирамиды
А ₁ (–1, 0, 1), А ₂ (2, 3, 1), А ₃ (0, –2, 2), А ₄ (1, –1, 5). Продолжение задания 5 пункты д—з.

Требуется найти:

д) уравнения прямых А ₁ А ₂ и А ₁ А ₃;

е) уравнения плоскостей А ₁ А ₂ А ₃ и А ₁ А ₂ А ₄;

ж) угол между плоскостями А ₁ А ₂ А ₃ и А ₁ А ₂ А ₄;

з) высоту пирамиды.

Решение:

д) Для нахождения уравнений прямых А ₁ А ₂ и А ₁ А ₃ используем уравнение (24) прямой, проходящей через две точки А ₁ (–1, 0, 1) и А ₂ (2, 3, 1):

А ₁ А ₂: или

Замечание. Отношение понимаем в том смысле, что и числитель этого отношения равен 0 и значит z = 1 для каждой точки прямой. Это означает, что прямая А ₁ А ₂ параллельна плоскости ОХУ и удалена от этой плоскости на расстояние z = 1.

Уравнение прямой А ₁ А ₂ можно записать в виде:

или как линию пересечения двух плоскостей .

А ₁ А ₃: или

е) уравнения плоскостей А ₁ А ₂ А ₃ и А ₁ А ₂ А ₄ получим, используя уравнение плоскости, проходящей через три данные точки А ₁ (–1, 0, 1),
А ₂ (2, 3, 1), А ₃ (0, –2, 2) формула (23):

или

Раскладывая определитель по элементам первой строки, получим:

Делим все члены уравнения на 3 и раскрываем скобки:

Окончательно уравнение плоскости А ₁ А ₂ А ₃ имеет вид:

Аналогично составляем уравнение плоскости А ₁ А ₂ А ₄.

А ₁ (–1, 0, 1), А ₂ (2, 3, 1), А ₄ (1, –1, 5)

или

А ₁ А ₂ А ₄:

ж) Чтобы определить угол между плоскостями А ₁ А ₂ А ₃ и А ₁ А ₂ А ₄ нужно найти их нормальные векторы. Уравнение плоскости А ₁ А ₂ А ₃ из предыдущей задачи имеет вид

Следовательно, нормальный вектор плоскости имеет координаты равные коэффициентам при х, у, z в уравнении плоскости,
т. е.

Из уравнения плоскости А ₁ А ₂ А ₄: определим координаты нормального вектора этой плоскости

Используем формулу (29):

з) Высоту пирамиды (отрезок А ₄ А ₅ (рис. 1)) можно определить как расстояние точки А ₄ (1, –1, 5) до плоскости А ₁ А ₂ А ₃.

А ₁ А ₂ А ₃:

Точка А ₄ (1, –1, 5).

В уравнение плоскости вместо х, у, z подставим координаты А ₄ и поделим .