
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Корреляционный анализ
|
|
В экономических исследованиях одной из важных задач является анализ зависимостей между изучаемыми переменными. Зависимость между переменными может быть либо функциональной, либо стохастической (вероятностной). Для оценки тесноты и направления связи между изучаемыми переменными при их стохастической зависимости пользуются показателями ковариации и корреляции.
Ковариацией cov(x, у) случайных величин Х и У называют среднее произведений отклонений каждой пары значений величин X иY в исследуемых массивах данных:
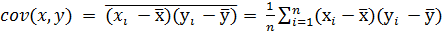 .
.
Ковариация есть характеристика системы случайных величин, описывающая помимо рассеивания величин X и Y еще и линейную связь между ними. Доказано, что для независимых случайных величин X и Y их ковариация равна нулю, а для зависимых случайных величин она отличается от нуля (хотя и не обязательно). Поэтому ненулевое значение ковариации означает зависимость случайных величин. Однако обращение в нуль ковариации не гарантирует независимости, бывают зависимые случайные величины, ковариация которых равна нулю. Из формулы определения ковариации видно, что ковариация характеризует не только зависимость величин, но и их рассеивание. Действительно, если, например, одна из величин X или Y мало отличается от своего математического ожидания (почти не случайна), то показатель ковариации будет мал, какой бы тесной зависимостью ни были связаны величины Х и Y. Так что обращение в нуль ковариации величин X и Y является не достаточным условием для их независимости, а только необходимым.
Использование ковариации в качестве меры связи признаков не совсем удобно, так как показатель ковариации не нормирован и при переходе к другим единицам измерения (например, от метров к километрам) меняет значение. Поэтому в статистическом анализе показатель ковариации сам по себе используется редко; он фигурирует обычно как промежуточный элемент расчета линейного коэффициента корреляции rxy:
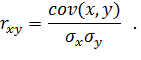
В 1889 г. Ф. Голтон высказал мысль о коэффициенте, который мог бы измерить тесноту связи между двумя коррелируемыми признаками. В начале 90-х гг. ХIХ в. Пирсон, Эджворт и Велдон получили формулу линейного коэффициента корреляции
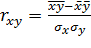 .
.
Линейный коэффициент корреляции характеризует степень тесноты не всякой, а только линейной зависимости. При нелинейной зависимости между явлениями линейный коэффициент корреляциитеряет смысл, и для измерения тесноты связи применяюттак называемое корреляционное отношение, известное также подназванием «индекс корреляции».
Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или убывать) по линейному закону. Эта тенденция к линейной зависимости может быть более или менее ярко выраженной, т. е. более или менее приближаться к функциональной. Если случайные величины X и Y связаны точной линейной функциональной зависимостью у=ax+b, то гxy = ± 1. В общем случае, когда величины X и Y связаны произвольной вероятностной зависимостью, линейный коэффициент корреляции принимает значение в пределах -1 < гxy< 1, тогда качественная оценка тесноты связи величин X и Y может быть выявлена на основе шкалы Чеддока(см. Рисунок 15).
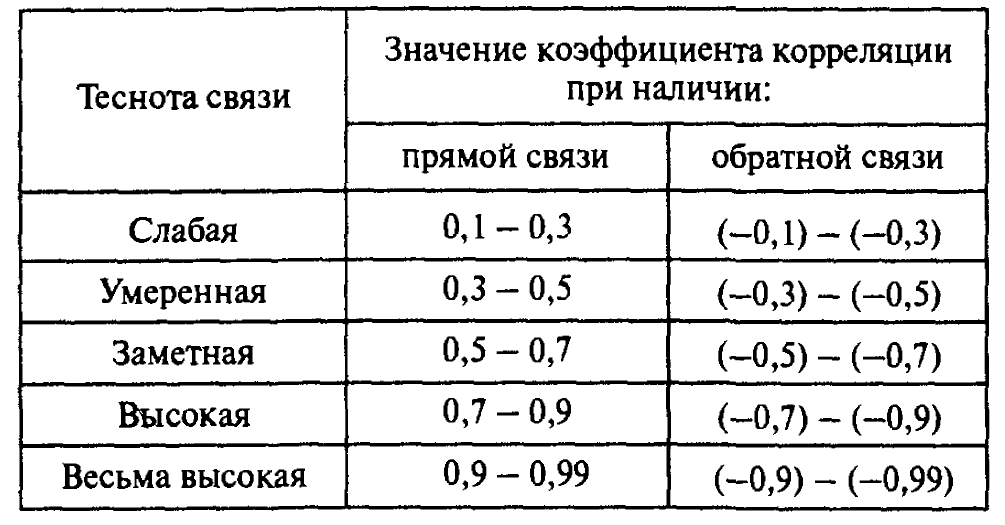
Рисунок 6 – Таблица Чеддока.
В теории разработаны и на практике применяются различные модификации формул расчета линейного коэффициента корреляции:
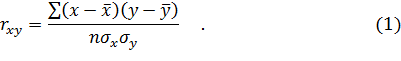
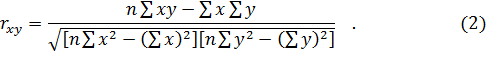
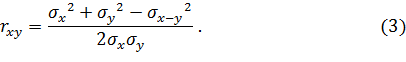
Приведенные формулы в определенных случаях имеют некоторые преимущества друг перед другом. Например, при небольших значениях n (n< 30) обычно употребляются формулы (2) и (3).
Необходимо обратить внимание, что формулы (1) - (3) справедливы для нахождения генерального коэффициента корреляции. Чтобы рассчитать выборочный коэффициент корреляции, необходимо в этих формулах генеральные средние заменить на выборочные средние, а генеральные стандартные отклонения - на выборочные стандартные отклонения.
Режим работы «Корреляция» предназначен для расчета генерального и выборочного коэффициентов корреляции соответственнона основе генеральных и выборочных данных.
Создаем новый лист. Переименовываем лист в «Корреляционный анализ». Копируем значения всех сопротивлений и значения всех токов.
Далее находим значимость коэфициента корреляции. Вводим значимость γ: 0, 95. Находим стандартоное отклонение по формуле:  , где n – число исследуемых элементов. Находим
, где n – число исследуемых элементов. Находим 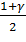 . Находим zкр: функция НОРМОБР(ссылка на значение «
. Находим zкр: функция НОРМОБР(ссылка на значение «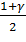 »; 0; ссылка на значение «стандартоное отклонение»). Найдем значение обратного преобразования Фишера: функция ФИШЕРОБР (ссылка на «zкр»). (см. Рисунок 7)
»; 0; ссылка на значение «стандартоное отклонение»). Найдем значение обратного преобразования Фишера: функция ФИШЕРОБР (ссылка на «zкр»). (см. Рисунок 7)
| гамма | (1+гамма)/2 | Zкр | станд.откл | n | rкр |
| 0, 95 | 0, 975 | 0, 248916 | 0, 127000127 | 0, 243899 |
Рисунок 7 - Значимость коэффициента корреляции
Создаем таблицу корреляции. Для этогона ленте выбираем вкладку «Формулы» – «Другие формулы»– «Статистические», выбираем «КОРРЕЛ». В появившемся окне в «массив1» задаем диапозон значений соответствующего сопровтивления, в «массив2» задаем диапозон значений соответствующего тока, и протягиваем для всех токов. Проводим эту процедуру для каждого сопротивления.
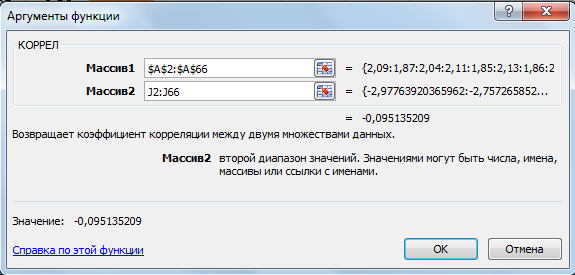
Рисунок 8–формула корреляции
Далее задаем цвета для каждой степени тесноты связи в таблице Чеддока (см. Рисунок 9). Заливку делаем на вкладке «Главная», группе «Шрифт»– «Формат ячеек». Также добавляем к таблице Чеддока строки для значения обратного преобразования Фишера значимостями 0, 95. Значимые значения выделяем внешней границей.
| слабая | 0, 1≤ |r|< 0, 3 |
| умеренная | 0, 3≤ |r|< 0, 5 |
| заметная | 0, 5≤ |r|< 0, 7 |
| высокая | 0, 7≤ |r|< 0, 9 |
| весьма высокая | 0, 9≤ |r|< 0, 99 |
| |r|> 0, 243899 |
Рисунок 9 – Преобразованная таблица Чеддока.
Создаем правила для всех ячеек таблицы в соответсвии с таблицей Чеддока (см. Рисунок 9). Для этого на вкладке «Главная», группе элементов «Стили» выбираем «Условное форматирование» - «Управление правилами». Нажимаем создать правило. Выбираем строку «Использовать формулу для определения форматируемых ячеек». В строке «Форматировать значения, для которых следующая формула является истинной» вводим формулу: =И(0, 1< =ссылка на диапазон ячеек таблицы< 0, 3). Нажимаем «Формат» и в появившемся окне на вкладке «Заливка» выбираем нужные параметры цвета и штриховки. Анологично поступаем для других степеней тесноты связи (см. Рисунок 10).
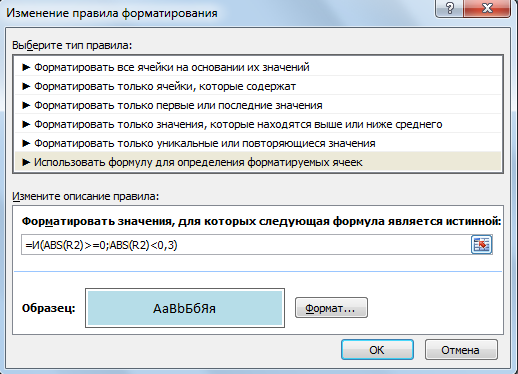
Рисунок 10 – Создание правил форматирования
В итоге получим таблицу Корреляции:
| I1 | I2 | I3 | I4 | I5 | I6 | |
| r01 | 0, 176758 | 0, 048543 | 0, 085786 | 0, 098609 | -0, 14229 | 0, 026064 |
| r02 | 0, 015872 | 0, 01315 | -0, 00397 | 0, 049675 | 0, 0763 | 0, 028189 |
| R1 | -0, 06915 | 0, 122426 | -0, 22135 | -0, 09836 | -0, 07479 | -0, 2536 |
| R2 | 0, 004218 | -0, 03812 | 0, 054205 | 0, 10252 | 0, 215184 | 0, 145115 |
| R3 | 0, 089329 | 0, 289367 | -0, 30832 | 0, 179823 | 0, 211744 | -0, 22004 |
| R4 | -0, 07649 | -0, 19429 | 0, 192984 | -0, 10899 | -0, 08314 | 0, 158554 |
| R5 | 0, 069517 | 0, 107547 | -0, 08372 | 0, 027622 | -0, 08032 | -0, 11786 |
| R6 | 0, 05354 | 0, 039505 | -0, 00695 | 0, 063202 | 0, 029637 | 0, 005525 |
Рисунок 10 – Корреляция