
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Регрессионный анализ
|
|
Регрессионный анализ, заключается в определении аналитического выражения связи зависимости случайной величины Y с независимыми случайными величинами X1, X2, …Xm. Форма связи результативного признака Y с факторами X1, X2, …Xm, получила название уравнения регрессии. В зависимости от типа выбранного уравнения различают линейную и нелинейную регрессию. В зависимости от числа взаимосвязанных признаков различают парную и множественную регрессию.
При изучении регрессии следует придерживаться определенной последовательности этапов:
1. Знание аналитической формы уравнения регрессии и определение параметров регрессии.
2. Определение в регрессии степени стохастической взаимосвязи результативного признака и факторов, проверка общего качества уровня регрессии.
3. Проверка статистической значимости каждого коэффициента уравнения регрессии и определения их доверительных интервалов.
Этап 1:
Уравнение линейной множественной регрессии имеет вид:

где  - теоретические значения результативного признака, полученные путем подстановки соответствующих значений факторных признаков в уравнение регрессии;
- теоретические значения результативного признака, полученные путем подстановки соответствующих значений факторных признаков в уравнение регрессии;
 ,
,  ,
,  - значения факторных признаков;
- значения факторных признаков;
 ,
,  ,
,  - - параметры уравнения (коэффициенты регрессии).
- - параметры уравнения (коэффициенты регрессии).
Параметры уравнения регрессии могут быть определены с помощью метода наименьших квадратов (именно этот метод и используется в MicrosoftExcel). Сущность данного метода заключается в нахождении параметров модели (ai), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии, т е.

Рассматривая S в качестве функции параметров аi, - и проводя математические преобразования (дифференцирование), получаем систему нормальных уравнений с т неизвестными (по числу параметров аi):

Рисунок 21 – Система нормальных уравнений.
Решив систему уравнений, находим значения параметров аi являющихся коэффициентами искомого теоретического уравнения регрессии.
Этап 2:
Для определения величины степени стохастической взаимосвязи результативного признака Y и факторов X необходимо знать следующие дисперсии:
• общую дисперсию результативного признака 7, отображающую влияние как основных, так и остаточных факторов:

где  - среднее значение результативного признака Y.
- среднее значение результативного признака Y.
• факторную дисперсию результативного признака Y, отображающуювлияние только основных факторов:

• остаточную дисперсию результативного признака Y, отображающуювлияние только остаточных факторов:

При корреляционной связи результативного признака и факторов выполняется соотношение:

Для анализа общего качества уравнения линейной многофакторной регрессии используют обычно множественный коэффициент детерминации R2, называемый также квадратом коэффициента множественной корреляции R. Множественный коэффициент детерминации рассчитывается по формуле:

- этот коэффициент характеризует адекватность построения модели.
Так как в большинстве случаев уравнение регрессии приходится строить на основе выборочных данных, то возникает вопрос об адекватности построенного уравнения генеральным данным. Для этого проводится проверка статистической значимости коэффициента детерминации R2 на основе F-критерия Фишера:

где n - число наблюдений;
т - число факторов в уравнении регрессии.
В математической статистике доказывается, что если гипотеза H0: R2 = 0 выполняется, то величина F имеет F-распределение с к = т и l=n-m-1 числом степеней свободы.
Гипотеза H0: R2 = 0 о незначимости коэффициента детерминации R2 отвергается, если  .
.
При значениях R > 0, 7 считается, что вариация результативного признака Y обусловлена в основном влиянием включенных в регрессионную модель факторов X.
Для оценки адекватности уравнения регрессии часто также используют показатель средней ошибки аппроксимации:

Этап 3:
Возможна ситуация, когда часть вычисленных коэффициентов регрессии не обладает необходимой степенью значимости, т.е. значения данных коэффициентов будут меньше их стандартной ошибки. В этом случае такие коэффициенты должны быть исключены из уравнения регрессии. Поэтому проверка адекватности построенного уравнения регрессии наряду с проверкой значимости коэффициента детерминации R2 включает в себя также и проверку значимости каждого коэффициента регрессии.
Значимость коэффициентов регрессии проверяется с помощью t-критерия Стьюдента:

где  - стандартное значение ошибки для коэффициента регрессии
- стандартное значение ошибки для коэффициента регрессии 
В математической статистике доказывается, что если гипотеза H0: R2 = 0
выполняется, то величина t имеет распределение Стьюдента с k: = п—т-1 числом степеней свободы, то есть:

Гипотеза H0: R2 = 0 о незначимости коэффициента регрессии отвергается, если 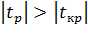 .
.
Кроме того, зная значениеtкр, можно найти границы доверительныхинтервалов для коэффициентов регрессии:


В программе Excel множественная линейная регрессия проводится с помощью инструмента регрессия пакета анализа.
Факторами регрессии являются сопротивления в цепи. Выходным параметром является ток. С помощью инструмента регрессия выводим графики остатков, нормированной вероятности, подборов.
Стандартная ошибка считается по формуле:

Проводя регрессионный анализ в программе Excel, мы копируем все исходные данные сопротивлений и один ток. Таблицу «Регрессионная статистика» получаем с помощью пакета анализа инструмента регрессия. За входной интервал Y выбирается значение тока, за входной интервал X значение всех сопротивлений. Выводим графики остатков, нормальной вероятности, подборов.

Рисунок22– Пакет анализа «Регрессия»
| Регрессионная статистика | |
| Множественный R | 0, 999311136 |
| R-квадрат | 0, 998622746 |
| Нормированный R-квадрат | 0, 998425996 |
| Стандартная ошибка | 0, 014371973 |
| Наблюдения |
Множественный R –это - коэффициент корреляцииR
R-квадрат – коэффициент детерминации R2
Стандартная ошибка считается по формуле:
 .
.
| Дисперсионный анализ |
 Столбец df– число степеней свободы равное 8.
Столбец df– число степеней свободы равное 8.
Для строки регрессия число степеней свободы определяется количеством факторных признаков m в уровне регрессии kф=m.
Для строки остаток число степеней свободы определяется числом наблюдений n и количеством переменных в уравнении регрессии m+1: k0=n-(m+1). Для строки итого число степеней свободы определяется суммой ky=kф+k0
Столбец SS– сумма квадратов отклонений Для строки регрессия – эта сумма квадратов отклонений теоретических данных от среднего:
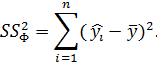
Для строки остаток – эта сумма квадратов отклонений эмпирических данных от теоретических:

Для строки итого – эта сумма квадратов отклонения эмпирических данных от среднего:
 .
.
Столбец МS- дисперсии, рассчитываемые по формуле:
 .
.
Для строки регрессия – это факторная дисперсия  .
.
Для строки остаток – это остаточная дисперсия  .
.
Столбец F – расчетное значение F-критерия Фишера.

Столбец значимости F – значение уровня значимости, соответствующее вычисляемому значению Fp. Так как F= 5, 48E-74, т.е. F> Значимость F, то множественный коэффициент детерминации существенно больше нуля.
Таблица сигнетированных коэффициентов регрессии ai и их статистические оценки:

Выводы
Инструмент «Описательная статистика» позволил создать статистический отсчет, содержащий информацию о центральной тенденции изменчивости входных данных.
В программе Microsoft Excel получили модель электрической цепи с помощью, которой можно легко рассчитать значения токов при изменяющихся сопротивлениях.
Корреляционный анализ позволил установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связанных с большими значениями другого набора (положительная корреляция), или, наоборот малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связанны (нулевая корреляция).
Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных.
Выведена формула  , с помощью которой можно провести различные исследования, например, определить влияние случайной величины на ток. В результате нашли абсолютную и относительную погрешности расчётов.
, с помощью которой можно провести различные исследования, например, определить влияние случайной величины на ток. В результате нашли абсолютную и относительную погрешности расчётов.