
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Детерминированные эквиваленты вероятностных ограничений
|
|
Применение традиционных методов решения требует преобразования вероятностных ограничений в соответствующие им детерминированные эквиваленты. Известно, что обычно этот процесс реализовать весьма непросто и успешным он бывает лишь в отдельных специальных случаях. Рассмотрим вероятностное ограничение, записанное в следующем виде:
 . (6.14)
. (6.14)
Ясно, что
(I) вероятностные ограничения (6.2) представляют собой набор ограничений вида (6.14);
(II) стохастическое ограничение на целевую функцию 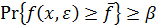 совпадает с ограничением вида (6.14), если ввести определение
совпадает с ограничением вида (6.14), если ввести определение  ;
;
(III) стохастическое ограничение на целевую функцию 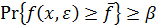 совпадает с ограничением вида (6.14), если ввести определение
совпадает с ограничением вида (6.14), если ввести определение  ;
;
(IV) стохастические ограничения на цели 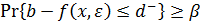 и
и 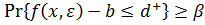 совпадают с ограничением вида (6.14), если ввести определения
совпадают с ограничением вида (6.14), если ввести определения 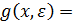 b-
b- 
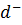 и
и 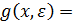
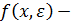 b -
b -  , соответственно и
, соответственно и
(V) стохастические ограничения на цели 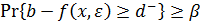 и
и 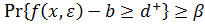 совпадают с ограничением вида (6.14), если ввести определения
совпадают с ограничением вида (6.14), если ввести определения 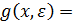
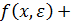
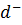 - b и
- b и 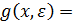
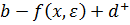 , соответственно.
, соответственно.
В этом разделе приведена сводка ряда известных результатов.
Теорема 6.1. Пусть случайный вектор  вырождается в случайную величину
вырождается в случайную величину  с функцией распределения Ф, а функция
с функцией распределения Ф, а функция  имеет вид
имеет вид  = h(x)-
= h(x)- 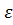 . Тогда
. Тогда 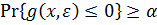 будет втом и только в том случае, если h(x)
будет втом и только в том случае, если h(x) 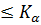 , где
, где  .
.
Доказательство: Предположим, что неравенство 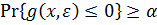 может быть записано в следующем виде
может быть записано в следующем виде
 . (6.15)
. (6.15)
Ясно, что для каждого заданного доверительного уровня 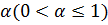 существует некоторое число
существует некоторое число 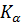 (таких чисел может быть несколько или даже бесконечно много) такое, что
(таких чисел может быть несколько или даже бесконечно много) такое, что
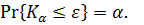 (6.16)
(6.16)
и вероятность 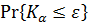 будет возрастать, если заменить
будет возрастать, если заменить 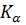 меньшим числом. Поэтому
меньшим числом. Поэтому  тогда и только тогда, когда
тогда и только тогда, когда 
Отметим, что равенство 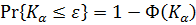 удовлетворяется всегда. Следовательно, в соответствии с (6.16),
удовлетворяется всегда. Следовательно, в соответствии с (6.16),
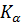 =
= 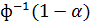 ,
,
где 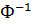 – обратная функция для Ф. В ряде случаев решение уравнения (6.16) будет не единственным, что равносильно многозначности функции
– обратная функция для Ф. В ряде случаев решение уравнения (6.16) будет не единственным, что равносильно многозначности функции 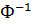 . В такой ситуации следует выбирать решение, наибольшее из имеющихся, т.е.
. В такой ситуации следует выбирать решение, наибольшее из имеющихся, т.е.

Таким образом, требуемым детерминированным эквивалентом является  . Теорема доказана.
. Теорема доказана.
Предположим, что имеются следующие вероятностные ограничения:
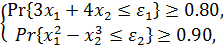 (6.17)
(6.17)
где  – экспоненциально распределенная случайная величина EXP(2), распределение вероятностей для которой обозначим как
– экспоненциально распределенная случайная величина EXP(2), распределение вероятностей для которой обозначим как 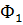 , а
, а 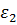 – нормально распределенная случайная величина N(2, 1), распределение вероятностей для нее обозначим как
– нормально распределенная случайная величина N(2, 1), распределение вероятностей для нее обозначим как 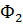 , Из теоремы 6.1. следует, что вероятностные ограничения (6.17) эквивалентны детерминированным ограничением вида
, Из теоремы 6.1. следует, что вероятностные ограничения (6.17) эквивалентны детерминированным ограничением вида
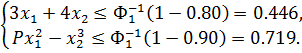
Теорема 6.2. Пусть имеется случайный вектор  , а функция g(x,
, а функция g(x,  ) принимает вид g(x,
) принимает вид g(x,  )=
)=  . Если
. Если  и bпредставляют собой независимые нормально распределенные случайные величины, тогда
и bпредставляют собой независимые нормально распределенные случайные величины, тогда 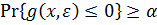 тогда и только тогда, когда
тогда и только тогда, когда
 , (6.18)
, (6.18)
где Ф – нормированное нормальное распределение.
Доказательство: Вероятностное ограничение 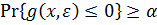 может быть записано в следующем виде
может быть записано в следующем виде
Pr 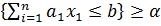 . (6.19)
. (6.19)
Поскольку 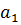 и b предполагаются независимыми нормально распределенными случайными величинами, функция
и b предполагаются независимыми нормально распределенными случайными величинами, функция
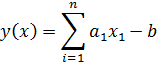
Также является нормально распределенной функцией со следующими значениями математического ожидания и дисперсии
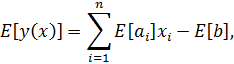
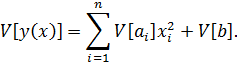
Отметим, что случайная величина
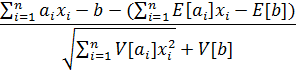
Должна быть нормированной нормально распределенной, т.е. иметь вид N(0, 1). Поскольку неравенство  эквивалентно выражению
эквивалентно выражению
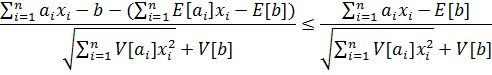
Вероятностное ограничение (6.19) эквивалентно ограничению
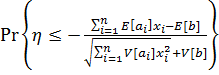 (6.20)
(6.20)
Где 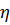 - нормированная нормально распределенная случайная величина. Итак, вероятностное ограничение (6.20) удовлетвориться только тогда и только тогда, когда
- нормированная нормально распределенная случайная величина. Итак, вероятностное ограничение (6.20) удовлетвориться только тогда и только тогда, когда
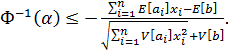 (6.21)
(6.21)
Отсюда следует, что детерминированным эквивалентом рассматриваемого вероятностного ограничения является выражение (6.18). Теорема доказана.
Предположим, например, что вероятностное ограничение имеет следующий вид
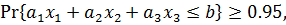 (6.22)
(6.22)
где 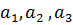 и b – нормально распределенные величины N(1.1), N(2.1), N(3.1) и N(4.1), соответственно. Тогда формула (6.18) позволяет получить детерминированный эквивалент для ограничения (6.22), который примет вид
и b – нормально распределенные величины N(1.1), N(2.1), N(3.1) и N(4.1), соответственно. Тогда формула (6.18) позволяет получить детерминированный эквивалент для ограничения (6.22), который примет вид

учитывая тот факт, что 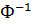 (0.95)=1.645.
(0.95)=1.645.