Детерміновані еквіваленти імовірнісних обмежень

Застосування традиційних методів вирішення вимагає перетворення імовірнісних обмежень у відповідні їм детерміновані еквіваленти. Відомо, що зазвичай цей процес реалізувати вельми непросто і успішним він буває лише в окремих спеціальних випадках. Розглянемо імовірнісне обмеження, записане в наступному вигляді:

. (6.14)

Ясно, що

(I) імовірнісні обмеження (6.2) являють собою набір обмежень виду (6.14);

(II) стохастичне обмеження на цільову функцію збігається з обмеженням виду (6.14), якщо ввести визначення ;

(III) стохастичне обмеження на цільову функцію збігається з обмеженням виду (6.14), якщо ввести визначення ;

(IV) стохастичні обмеження на цілі и збігаються з обмеженням виду (6.14), якщо ввести визначення b- и b - , відповідно і

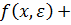
(V) стохастичні обмеження на цілі та збігаються з обмеженням виду (6.14), якщо ввести визначення - b и , відповідно.

У цьому розділі наведена зведення ряду відомих результатів. Теорема 6.1. Нехай випадковий вектор ε вироджується в випадкову величину ε з функцією розподілу Ф, а функція g (x, ε) має вигляд g (x, ε) = h (x) - ε. Тоді Pr {g (x, ε) ≤ 0} ≥ α буде втом і тільки в тому випадку, якщоh(x) , де .

Доказ: Припустимо, що нерівність Pr {g (x, ε) ≤ 0} ≥ α може бути записано в наступному вигляді

. (6.15)

Ясно, що для кожного заданого довірчого рівня α (0 < α ≤ 1) існує деяке число (таких чисел може бути кілька або навіть нескінченно багато) таке, що

(6.16)

і ймовірність Pr {K_α ≤ ε } буде зростати, якщо замінити меншим числом. Тому Pr {h (x) ≤ ε } ≥ α тоді і тільки тоді, коли

Відзначимо, що рівність задовольняється завжди. Отже, відповідно до (6.16),

= ,

де – зворотна функція для Ф. У ряді випадків рішення рівняння (6.16) буде не єдиним, що рівносильно багатозначності функції . У такій ситуації слід вибирати рішення, найбільшу з наявних, тобто

Таким чином, необхідним детермінованим еквівалентом є . Теорема доведена.

Припустимо, що є наступні імовірнісні обмеження:

(6.17)

де – експоненціально розподілена випадкова величина EXP (2), розподіл ймовірностей для якої позначимо як , а – нормально розподілена випадкова величина N (2, 1), розподіл ймовірностей для неї позначимо як , З теореми 6.1. випливає, що імовірнісні обмеження (6.17) еквівалентні детермінованим обмеженням виду

Теорема 6.2. Нехай є випадковий вектор , а функц і я g(x, ) прийа є вид g(x, )= . Якщо 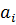та b представляють з себе незалежні нормально розподілені випадкові величини, тоді тоді і тільки тоді, коли

, (6.18)

де Ф – нормоване нормальний розподіл.

Доказ: Імовірнісне обмеження Pr {g (x, ε) ≤ 0} ≥ α може бути записано в наступному вигляді

Pr 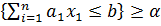. (6.19)

Оскільки и b передбачаються незалежними нормально розподіленими випадковими величинами, функція

Також є нормально розподіленою функцією з наступними значеннями математичного сподівання і дисперсії

Відзначимо, що випадкова величина

Повинна бути нормованою нормально розподіленої, тобто мати вигляд N (0, 1). оскільки нерівність 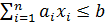еквівалентно выразу

Імовірнісне обмеження (6.19) еквівалентно обмеженню

(6.20)

Де η -нормована нормально розподілена випадкова величина. Отже, ймовірнісний обмеження (6.20) задовольнитися тільки тоді і тільки тоді, коли

(6.21)

Звідси випливає, що детермінованим еквівалентом розглянутого імовірнісного обмеження є вираз (6.18). Теорема доведена.

Припустимо, наприклад, що імовірнісне обмеження має наступний вигляд

(6.22)

де 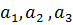и b – нормально розподілені величини N (1.1), N (2.1), N (3.1) і N (4.1), відповідно. Тоді формула (6.18) дозволяє отримати детермінований еквівалент для обмеження (6.22), який матиме вигляд

Враховуючи той факт, що (0.95)=1.645.