Теорема эквівалентності

У попередньому розділі ми обговорили детерміновані еквіваленти імовірнісних обмежень. Тут же розглянемо деякі властивості наступній спеціальній РСР-моделі

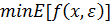(6.23)

при наявності імовірнісних обмежень

(6.24)

де x-вектор рішень, ε -випадковий вектор з щільністю розподілу ймовірностей Ф (ε). Визначимо нову функцію від (x, u) таким чином:

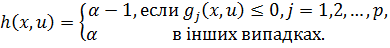(6.25)

Таким чином, для кожного зафіксованого рішення x функція h (x, u) приймає значення α -1 на області

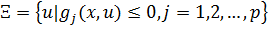
і значення α на доповненні з безлічі. Тоді з визначення оператора математичного очікування випливає, що

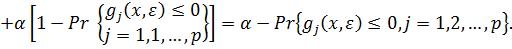
Тому, нерівність E [h (x, ε)] ≤ 0 задовольняється тоді і тільки тоді, коли задовольняються імовірнісні обмеження (6.24). Цей факт встановлює взаємозв'язок між моделями EVM і РСР, яка може бути сформульована у вигляді наступної теореми.