Теплопроводность цилиндрической стенки

Рассмотрим однослойную цилиндрическую стенку (трубу, рис. 1.5) длиной l с коэффициентом теплопроводности 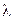, внутренним 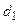и наружным 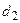диаметрами, а также температурами стенки на внутренней 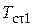и наружной 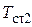поверхностях. Будем считать, что l > > 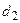, и поэтому теплота распространяется практически только в радиальном направлении. Следовательно, изотермические поверхности в данной стенке имеют форму цилиндров, ось которых совпадает с осью трубы.

Согласно формулам Q = q∙ F и закону Фурье 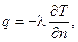тепловой поток через цилиндрическую поверхность с произвольным радиусом r и площадью равен:

Q = .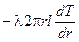

При стационарном режиме значение Q по радиусу не изменяется. Тогда из этой формулы интегрированием легко получить уравнение температурного поля в цилиндрической стенке

Т = .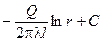

Отсюда видно, что изменение температуры по толщине цилиндрической стенки подчиняется логарифмическому закону, как показано на рис. 1.5. Градиент температуры dT/dr уменьшается (по абсолютной величине) по мере приближения к наружной поверхности стенки. Это объясняется уменьшением плотности теплового потока по радиусу, поскольку тепловой поток Q постоянен, а площадь изотермической поверхности с ростом r увеличивается.

Подставив в полученную формулу значения температур на границах стенки (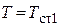 при r = r 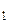и 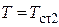при r = r 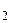) и заменив отношение r 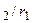на 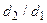, получим

Q = .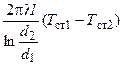

Тепловой поток через единицу длины трубы называется линейной плотностью теплового потока. Он обозначается через и равен

= ,

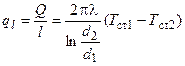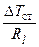где - линейное тепловое сопротивление стенки.

Итак, линейная плотность теплового потока через цилиндрическую стенку пропорциональна температурному напору на стенке и обратно пропорциональна её линейному тепловому сопротивлению.

Если труба тонкостенная (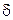 < < 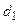), то кривизна стенки слабо влияет на значение линейной плотности теплового потока. В этом случае для её определения можно использовать зависимость, полученную для плоской стенки:

Q 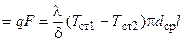и соответственно ,

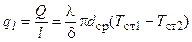где 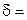0, 5(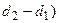 - толщина стенки; 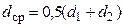- средний диаметр стенки.