Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Наезд на пешехода, движущегося под произвольным углом
|
|
Рассмотренные выше разновидности наезда — поперечный (a =90°), попутный (а =0) и встречный (а = 180°)—являются частными случаями. Рассмотрим методику экспертного исследования наезда, при котором векторы скоростей Ua и Uп пересекались под некоторым углом 
0 (рис. 5.15, а). Автомобиль двигался без торможения и ударил пешехода торцовой частью. Обзорность и видимость неограниченны, угол а < 90° (вариант А-11-2).
Пешеход от границы опасной зоны до наезда прошел путь Sп= (
y+ly)/sin а. Автомобиль за это время переместился на расстояние
(5.38)
Время с момента возникновения опасной обстановки до наезда на пешехода в процессе ДТП tп= ( у+ ly)/(Uп sin a).
Расстояние между автомобилем и пешеходом в момент возникновения опасной обстановки, измеренное по направлению движения автомобиля (расстояние конкретной видимости пешехода), согласно рис. 5.14 Sв=Sа—Sп cos а =(Ua — Uп cos a) tп. Своевременно применив экстренное торможение, водитель может обеспечить безопасность двумя способами:
если скорость автомобиля уменьшится до Uп cos a;
Рис. 5.15. Схема косого наезда на пешехода:
а— а < 90°, б—предположительная версия, в— 90° < а < 180°
если за время торможения пешеход к моменту приближения автомобиля успеет уйти с его полосы движения.
Предположительную версию рассматриваемого ДТП иллюстрирует рис. 5.15, 6. Если водитель начнет реагировать на пешехода в момент пересечения им границы опасной зоны (положение /), то за время Т автомобиль продвинется на расстояние UaT, а пешеход пройдет путь UaT (положение //). Затем автомобиль начнет двигаться замедленно. В некоторый момент времени t перемещение точки А, находящейся на расстоянии у от правой стороны автомобиля, S'a =UaT+Uat—jt2/2.
Проекция пути, пройденного пешеходом через время t, на направление движения автомобиля S'п cos a =Uп cos a (T+ t).
Если автомобиль, несмотря на торможение, войдет в контакт с пешеходом, то S'a=Sв+S'п cos a. Подставив сюда значения S'a, Sв и S'п, после преобразований имеем
(5.39)
Если решение этого уравнения дает комплексные корни, то контакт автомобиля с пешеходом невозможен: автомобиль остановится раньше, чем его передняя часть достигнет траектории пешехода. Следовательно, можно сделать вывод о том, что водитель, затормозив, мог избежать наезда на пешехода. Если получим один корень, то скорость заторможенного автомобиля в момент контакта с пешеходом снизится до Uп cos a и сила удара будет относительно невелика. Наконец, два действительных корня уравнения (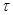
1 и 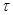2) свидетельствуют о том, что автомобиль даже при своевременном торможении не остановится у линии следования пешехода, а пересечет ее с некоторой скоростью. Физический смысл имеет меньший корень уравнения: 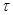1.
Однако наличие действительных корней еще не дает оснований для вывода о невозможности предотвратить наезд, так как автомобиль имеет ограниченные размеры и пешеход мог уйти с полосы его движения за время t1. Возможность безопасного перехода проверяем следующим образом.
Путь пешехода в случае экстренного торможения автомобиля S'п=Uп (T+ 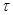1). Расстояние от правой габаритной стороны автомобиля до точки контакта его с пешеходом в предположительной версии ДТП l'у= =Uп (T+ 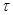1)sin a — y.
Размер l'у не может быть меньше расстояния l'у, так как время движения заторможенного автомобиля больше времени его равномерного движения. С другой стороны, максимальное значение этого размера с учетом безопасного интервала равно Ва+ б. Следовательно, наезд неизбежен при условии l у < l'у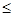 
Ва + б.
Если данное условие не выполнено и l'у> Bа+ б, то пешеход к моменту приближения к нему автомобиля уже находился бы вне полосы движения последнего. В этом случае можно сделать вывод о том, что водитель мог избежать наезда на пешехода, если бы своевременно затормозил.
Уравнение (5.39) можно применить и для исследования косого встречного наезда, при котором пешеход не удаляется от автомобиля, а приближается к нему. В этом случае 90° < a < 180°. Однако на практике удобнее использовать дополнительный угол 
=180°— а. Тогда уравнение (5.15в) принимает следующий вид:
(540)
Анализ результатов решения уравнения (5 40) не должен представить затруднений При а = =90° приходим к варианту поперечного наезда, при а =0 ( =180°)— попутного наезда, при a =180° ( =0) — встречного наезда.
Предположительную версию косого наезда можно также проанализировать, используя понятия остановочного пути и времени При варианте наезда A-II-2 води
тель в процессе ДТП не тормозил. Если бы он своевременно затормозил, то при снижении скорости автомобиля до безопасного предела, т. е. от Ua до Uп cos a, прошло бы время t'a=T+ (Ua—Uп сos a)/j. Затормаживаемый автомобиль за это время переместился бы на расстояние S'a=Ua T+ (U2a—U2пcos2 а)/ (2j). Безопасность будет обеспечена при условии, что скорость автомобиля снизится до безопасного предела на пути, не превышающем удаление автомобиля:
где S'п=Uп t'a — путь пешехода за время t'а, т. е. в случае торможения автомобиля.
Подставив в последнее неравенство значения S'a, S'п и Sуд, получаем условие сохранения безопасности: tп — Т> (Ua — Uп COS а)/(2j).
Смысл этого неравенства очевиден. В левой части — промежуток времени, имеющегося в распоряжении водителя для снижения скорости. В правой части — время, минимально необходимое для этого снижения, обусловленное обстоятельствами ДТП и техническими возможностями автомобиля.
Рассмотрим условие безопасного перехода пешеходом полосы движения автомобиля. В этом случае скорость U'н, с которой автомобиль пересекает линию следования пешехода, больше Uпcos а.
Время и путь движения заторможенного автомобиля в интервале скорости Ua...U'н t' a=T+ (Ua—U'н)/j=S'п/Uп и S'а =UаТ+ (U2а—(U'н)2)/(2j). Исключив из этих выражений скорость U'н, приходим к формуле пути S'а=Ua S'п/Uп— (S'п/Uп—T)2j/2=Syд+S'п соs a. Подставив в эту формулу значение удаления Sуд=Uа—Uп cos а, после преобразования приходим к уравнению:
Отсюда S'п=Uп{T*+ T 
}.
Физический смысл имеет меньший корень уравнения со знаком «минус» перед радикалом.
Таким образом условие безопасного выхода пешехода за границу полосы движения автомобиля: S'п> ( y+ Ва + б)/sin а.
Таблица 5.2 Условия возможности снижения скорости автомобиля до безопасных пределов
Левая часть данного неравенства характеризует максимальный путь, который может пройти пешеход за время экстренного снижения скорости автомобиля от Ua ДО U' н
Правая часть формулы характеризует путь, который пешеходу необходимо пройти, чтобы выйти за пределы опасной зоны.
Таблица 5.3 Условия безопасного перехода опасной зоны
При а =0 (вариант А-I-2) правая часть неравенства обращается в бесконечность, т. е. безопасный переход невозможен ни при каких исходных данных. Это легко объяснимо: как бы долго ни двигался пешеход параллельно автомобилю, он все равно не уйдет с его полосы движения. При а =90° (перекрестный наезд, вариант A-III-2) для условия безопасного перехода получаем известное соотношение: S'п> у+ Ва+ б.
Аналогично можно прийти к формулам, выражающим условия безопасности для остальных разновидностей наезда. В табл. 5.2 приведены такие формулы для условий снижения скорости (до Uпcos a или до остановки), а в табл. 5.3 — для безопасного перехода опасной зоны. При этом принято обозначение Т* =(Uа—Uпcos a)/j=(Uа+ Uпcos )/j.
Формулы, приведенные в табл. 5.2 и 5.3, позволяют определить, была ли у водителя техническая возможность предотвратить наезд на пешехода.