
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Влияние выбираемых параметров на выводы эксперта
|
|
Выполняя экспертизы по уголовным делам, связанным с ДТП, эксперт-автотехник постоянно сталкивается с недостатком достоверно установленных данных и необходимостью действовать в условиях неопределенности. С одной стороны, следствие (или суд) не может определить значения некоторых технических параметров (например, коэффициентов (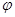 x, Кэ, замедления j и др.) и эксперт выбирает их самостоятельно. С другой стороны, многие численные значения, устанавливаемые следствием, имеют большой диапазон изменения, например, скорость автомобиля указывается в пределах 30...80 км/ч.
x, Кэ, замедления j и др.) и эксперт выбирает их самостоятельно. С другой стороны, многие численные значения, устанавливаемые следствием, имеют большой диапазон изменения, например, скорость автомобиля указывается в пределах 30...80 км/ч.
Результаты расчетов и конечные выводы эксперта существенным образом зависят от того, какие значения параметров он выберет при расчете. Лишенные возможности установить истинные значения параметров, характеризующих обстоятельства данного ДТП, эксперты нередко принимают для расчетов средние данные, не пытаясь определить, к каким последствиям приведет выбор завышенного (заниженного) значения того или иного коэффициента. Чтобы не допустить ошибок, следует иметь в виду, что категорический вывод о возможности
предотвращения ДТП можно сделать только в том случае, если в расчет введены наиболее благоприятные для водителя предельные значения выбираемых показателей. Категорический вывод об отсутствии такой возможности эксперт может сделать, лишь если расчеты проведены по предельным значениям, неблагоприятным для водителя. В остальных случаях все расчеты необходимо делать по двум вариантам с учетом верхнего и нижнего пределов изменений выбираемых данных. Выводы, полученные при этом, даже противоречивые (например, при коэффициенте сцепления 0, 8 водитель имел возможность предотвратить наезд на пешехода, а при коэффициенте сцепления 0, 6 не имел такой возможности) указываются в заключении эксперта. Окончательно их оценивает орган, назначивший экспертизу.
Любое ДТП — результат разрешения конфликтной ситуации, в которой интересы участников происшествия и соответственно оценка ими заключения эксперта, в особенности его выводов, часто диаметрально противоположны. Так, пострадавший от наезда пешеход вряд ли легко согласится с утверждением, что водитель не имел технической возможности избежать наезда. Водитель в свою очередь может возражать, если эксперт в своем заключении укажет на наличие у него такой возможности. Для определенности в дальнейшем будем оценивать выводы эксперта с позиции только одного из участников ДТП, а именно — водителя. В сложившейся практике ему как лицу, управляющему источником повышенной опасности, приходится выступать в роли ответчика независимо от того, кто является истинным виновником происшествия.
Анализируя возможность предотвращения поперечного наезда на пешеходов при прямолинейном движении автомобиля (т. е без учета маневра), эксперт последовательно определяет четыре условия безопасности:
своевременности действий водителя;
остановки автомобиля до линии следования пешехода;
безопасного перехода перед автомобилем;
безопасного проезда перед пешеходом.
Рассмотрим эти условия и попытаемся выяснить, как повлияет на выполнение каждого из них изменение (в ту или другую сторону) отдельных параметров, входящих в расчетные формулы. Примем при этом все обычные в экспертной практике ограничения и допущения (автомобиль заменяем прямоугольником, а пешехода — точкой, движение автомобиля считаем прямолинейным, а движение пешехода—равномерным и т. п.). Принимаем также, что направления движения автомобиля и пешехода взаимно перпендикулярны (поперечный наезд) и что удар пешеходу нанесен передней частью автомобиля. Для других вариантов наезда выводы не меняются по существу, но формулы получаются более громоздкими.
Начнем с наезда заторможенным автомобилем. Если водитель действовал правильно с технической точки зрения и своевременно реагировал на пешехода, то время tдн движения автомобиля до момента наезда по крайней мере не меньше времени движения пешехода: tдн 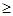 tп. Вместе с тем tдн=T+(Uа—Uн)/j; t п =Sп/Uп, следовательно Т+ (Uа—Uн)/j
tп. Вместе с тем tдн=T+(Uа—Uн)/j; t п =Sп/Uп, следовательно Т+ (Uа—Uн)/j 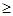 Sп/Uп.
Sп/Uп.
Скорости Ua и Uн выразим через расстояния Sю и Sпн, что вместе с последним неравенством дает:
 (5.41)
(5.41)
Время T1=T+ 0, 5t3=t1+ t2+ t3
Неравенство (5.41) представляет собой развернутое выражение для первого условия безопасности. Соблюдение неравенства тем более вероятно, чем меньше его левая часть, т. е. чем меньше расчетное значение замедления. Таким образом, чем меньше j, тем вероятнее вывод о том, что водитель в условиях данного ДТП действовал технически правильно и своевременно затормозил автомобиль. Однако замедление прямо пропорционально коэффициенту сцепления и обратно пропорционально коэффициенту эффективности торможения. Поэтому, выбирая меньшее значение x и большее значение Кэ, эксперт увеличивает вероятность благоприятного для водителя вывода, а выбирая большее значение 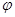 х и меньшее значение Кэ, он уменьшает эту вероятность.
х и меньшее значение Кэ, он уменьшает эту вероятность.
Для увеличения правой части неравенства (5.41) значение Uп должно быть по возможности большим, следовательно, при введении в расчет большего значения скорости пешехода увеличивается возможность вывода, благоприятного для водителя.
Размеры Sю, Sп, Sпн, как правило, устанавливаются следствием однозначно. Однако при недоброкачественном
осмотре места ДТП и невнимательном оформлении первичной документации возможны некоторые расхождения их значений. Введение в расчеты большего значения Sю и меньших значений Sп и Sпн приводит к большей вероятности вывода о том, что водитель в сложившейся дорожной обстановке своевременно реагировал на движение пешехода, т. е. действовал технически правильно.
Составим табл. 5.4, в которой отразим влияние различных факторов на возможность вывода, более благоприятного для водителя. Если большее значение какого-либо параметра (например, скорости пешехода) способствует такому выводу, то в таблице проставлен знак «+». Если же, напротив» благоприятному выводу соответствует уменьшение параметра (например, замедления автомобиля), то в таблице проставлен знак «—». Нуль означает, что изменение параметра не сказывается на выводах.
Если неравенство (5.41) не выполнено и эксперт устанавливает, что водитель опоздал принять меры к снижению скорости и остановке автомобиля, то рассматривается соблюдение второго условия. Водитель не имеет технической возможности остановить автомобиль до линии следования пешехода, если Sзап< Sпн.
На отрезке пути Sзап автомобиль движется равномерно, следовательно, Sзап= (tп—tдн)Uа< Sпн. Подставив в формулу значения tдн, Ua и tп, получаем: (0, 5t3j+  )[Sп/Uп- T1 -(
)[Sп/Uп- T1 -( —
—  )
)  ]< Sпн.
]< Sпн.
Возможность соблюдения этого неравенства тем очевиднее, чем меньше его левая часть, т. е. чем меньше j (при этом уменьшаются оба члена первой скобки и увеличивается значение дроби во второй скобке, что ведет к ее уменьшению). При увеличении j, напротив, вероятность нарушения неравенства возрастает, т. е. увеличивается возможность получения неблагоприятного для водителя ответа. Аналогичный результат получим,
Таблица 5.4. Влияние отдельных параметров на вывод, благоприятный для водителя при наезде в процессе торможения.
| Условия безопасности | j | 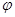 x x
| К э | Uп | Sп | Sю | Sпн |
| - | - | + | + | - | + | - | |
| — | — | + | + | — | + | + | |
| + | + | — | — | + | — | + | |
| + | + | — | — | + | — | + |
увеличивая значение скорости Uп и уменьшая путь Sп. Чем больше эта скорость и меньше путь пешехода, тем меньше левая часть выражения, а следовательно, и возможность благоприятного для водителя вывода.
Выбрав большие значения Sю и перемещения Sпн, эксперт увеличивает вероятность благоприятного для водителя вывода.
Таким образом, все рассмотренные параметры влияют на соблюдение второго условия так же, как на выполнение первого условия.
Рассматривая третье условие, эксперт отвечает на вопрос: «Имел ли водитель техническую возможность при своевременно предпринятом торможении пропустить пешехода перед автомобилем?». При этом подразумевается, что, хотя автомобиль, снижая скорость, не останавливается перед линией следования пешехода, последний все же успевает покинуть опасную зону. Наезд исключается вследствие увеличения времени движения автомобиля в заторможенном состоянии.
Математическая интерпретация условия безопасности с позиций, благоприятных для водителя, может быть представлена как S'п ( у+ Ва+
у+ Ва+  б).
б).
Определяем путь пешехода при своевременном торможении автомобиля

где t'дн — время движения автомобиля до линии следования пешехода при своевременно предпринятом торможении.
Здесь

где u'н — скорость, с которой автомобиль пересек бы эту линию;
S'пн — расстояние, на которое переместился бы автомобиль после пересечения этой линии.
Решая систему приведенных уравнений, получаем
 (5.42)
(5.42)
Данное условие легче выполняется при больших значениях замедления. Другими словами, чем меньше коэффициент Кэ и больше 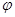 х, тем больше вероятность вывода о том, что водитель, даже своевременно затормозив, не имел технической возможности пропустить пешехода и избежать наезда на него.
х, тем больше вероятность вывода о том, что водитель, даже своевременно затормозив, не имел технической возможности пропустить пешехода и избежать наезда на него.
Влияние скорости пешехода на результаты анализа в этом случае совпадают с влиянием замедления j. Чем быстрее движется пешеход, тем больше у него шансов безопасно пересечь полосу следования автомобиля. Следовательно, выбор большего значения Uп и меньшего значения Sп уменьшает вероятность благоприятного для водителя вывода. К аналогичным результатам приводит увеличение параметра Sю и уменьшение значения Sпн.
Последнее (четвертое) условие безопасности не будет обеспечено, если задняя габаритная точка автомобиля пересекает линию следования пешехода позже, чем он дойдет до полосы движения автомобиля: (Sуд+ Lа)/Uа> ( у—
у—  б)/Uп. Подставим в это выражение значение
б)/Uп. Подставим в это выражение значение
удаления: [SпUa/Uп—(Ua—Uн)2/(2j)+La]/Ua> ( у—
у—  б )/Uп.
б )/Uп.
После приведения подобных членов получим [(Uа- U н)2 - 2La j]/(2jUa)< (Sп -  у +
у +  б)/Uп.
б)/Uп.
Анализируя последнее неравенство, можно прийти к выводу, что выполнение его тем вероятнее, чем меньше значения j, Uп и Sю и чем больше параметры Sп и Sпн.
Подведем некоторые итоги. Сводная табл. 5.4 свидетельствует о том, что изменение факторов, благоприятно сказывающееся на выполнении первых двух условий, отрицательно влияет на возможность выполнения последних неравенств. Однако, как указывалось выше, в практике экспертного анализа ДТП преимущественное распространение получило второе условие безопасности. Первое и третье условия рассматриваются относительно редко, а четвертое встречается лишь как исключение.
Рассмотрим несколько примеров.
Пример 1. Автомобиль ГАЗ-24 «Волга» совершил наезд на пешехода, двигавшегося поперек проезжей части. Покрытие дороги — мокрый асфальтобетон (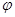 х =0, 35...0, 45), длина тормозного следа до задних колес Sю=24, 5 м. После наезда автомобиль переместился на Sпн=4, 5 м, пешеход прошел по проезжей части до места удара Sп=6 м.
х =0, 35...0, 45), длина тормозного следа до задних колес Sю=24, 5 м. После наезда автомобиль переместился на Sпн=4, 5 м, пешеход прошел по проезжей части до места удара Sп=6 м.
Своевременно ли водитель применил торможение?
Принимаем t1=0, 8 с; t2=0, 1с; t3=0, 1 с. Следовательно, T=0, 95 с; T1 =1, 0 с.
Решения. I Пусть скорость пешехода Uп=2 м/с, тогда время его перемещения до наезда tп=6, 0/2, 0=3, 0 с. При минимальных значениях (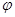 х=0, 35 и Kэ=1, 0 замедление j
х=0, 35 и Kэ=1, 0 замедление j  3, 5 м/с2 Тогда:
3, 5 м/с2 Тогда:
начальная скорость автомобиля Ua = 0, 05 • 3, 5 +  = 13, 3 м/с;
= 13, 3 м/с;
скорость автомобиля в момент наезда на пешехода Uп=  = 5, 6 м;
= 5, 6 м;
время движения автомобиля до наезда tдн= 0, 95+ (13, 3—5, 5)/3, 5= 3, 15 с.
Поскольку t п =3, 0 с < t дн =3, 15 с, водитель начал реагировать на действие пешехода даже несколько раньше, чем последний начал двигаться по проезжей части. Следовательно, водитель действовал технически правильно и своевременно реагировал на пешехода.
II. При том же значении К э но при максимальном значении коэффициента сцепления (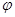 х=0, 45) замедление j
х=0, 45) замедление j  4, 5 м/с2. Тогда:
4, 5 м/с2. Тогда:
начальная скорость автомобиля Ua = 0, 05 • 4, 5 +  = 15, 05 м/с;
= 15, 05 м/с;
скорость автомобиля в момент наезда Uн=  =6, 35 м/с;
=6, 35 м/с;
время движения автомобиля до наезда tдн =0, 95+(15, 05—6, 35)/4, 5=2, 88 с.
Тот факт, что время движения пешехода (3, 0 с) превышает время движения автомобиля до наезда (2, 88 с), говорит о том, что водитель несколько запоздал с началом торможения, т. е. действовал несвоевременно.
III. Увеличив скорость движения пешехода, например до 3, 0 м/с, получаем tп=2, 0 с. Такое же значение получим при Uп=2 м/с, уменьшив путь пешехода до 4 м.
Из сопоставления tп (2, 0 с) с tдн (2, 88 с) ясно, что водитель начал реагировать на пешехода почти на 1 с раньше, чем возникла опасная обстановка. Таким образом, при увеличении скорости пешехода и уменьшении его пути возрастает вероятность получения вывода, благоприятного для водителя.
Теперь рассмотрим, как повлияет изменение отдельных параметров на вывод эксперта по второму условию (возможность остановки автомобиля до линии следования пешехода при своевременном торможении).
Пример 2. Рассмотрим ситуацию, описанную в предыдущем примере, и определим возможность остановки автомобиля до линии следования пешехода, если автомобиль после удара переместился на Sпн= =12 м, а Uп=2 м/с.
Решения. I. При минимальном значении замедления j=3, 5 м/с2;
начальная скорость автомобиля Uа=13, 3 м/с;
скорость автомобиля в момент наезда на пешехода Uн=  =9, 2 м/с;
=9, 2 м/с;
остановочный путь автомобиля So =0, 95*13, 34+ (13, 32)/7, 0= 12, 6 + 25, 3=37, 9 м;
удаление автомобиля от места наезда в момент возникновения опасной обстановки Sуд =13, 3*3, 0—(13, 3—9, 22)/7, 0= 37, 5 м.
Поскольку остановочный путь больше расстояния, разделявшего автомобиль и пешехода в момент возникновения опасной обстановки, то водитель не имел технической возможности остановить автомобиль до линии движения пешехода.
II. При неизменном значении скорости пешехода и замедлении j=4, 5 м/с2:
начальная скорость автомобиля составит 15, 05 м/с;
остановочный путь Sо = 0, 95 • 15, 05 +15, 052/9, 0 = 14, 3 + 25, 1 = 39, 4 м;
удаление автомобиля от места наезда Sуд= 15, 05-3, 0—(15, 05—
-10, 4)2/9, 0=42, 7 м.
Сравнивая полученные значения, можно прийти к выводу, что водитель имел техническую возможность остановиться до линии следования пешехода, поскольку расстояние, отделявшее автомобиль от пешехода (42, 7 м), значительно превышало остановочный путь автомобиля (39, 4 м).
III. Если скорость пешехода увеличится, например до 2, 5 м/с, время его движения уменьшается до 2, 4 с, а расстояние от автомобиля до места наезда—до 34, 65 м. Удаление Sуд= 15, 05 •2, 4—(15, 05— -10, 4)2/9, 0 =33, 65 м.
Поскольку удаление (33, 65 м) меньше остановочного пути (39, 4 м), то можно сделать вывод, что водитель даже при своевременном экстренном торможении не мог остановиться и предотвратить наезд на пешехода. Следовательно, и в этом случае увеличение Uп и уменьшение j приводят к более благоприятным для водителя выводам.
Перейдем к более простому для анализа виду ДТП:
водитель не снижал скорости, и автомобиль все время двигался равномерно.
Первое условие безопасности в данном случае: Sп/Uп 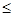 Т. Все входящие в это выражение показатели не зависят от j,
Т. Все входящие в это выражение показатели не зависят от j, 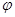 х и Кэ, следовательно, соблюдение первого условия не связано с их выбором, оно зависит лишь от, Sп и Uп. Значения отдельных составляющих Т нормированы и эксперт не вправе изменить их произ-волено.
х и Кэ, следовательно, соблюдение первого условия не связано с их выбором, оно зависит лишь от, Sп и Uп. Значения отдельных составляющих Т нормированы и эксперт не вправе изменить их произ-волено.
Второе условие безопасности можно выразить следующим образом (при ответе, благоприятном для водителя): Syд=UaSп/Un< So. Подставив значение остановочного пути после сокращения на Uа, придем к формуле:
 (5.43)
(5.43)
В отличие от предыдущего случая скорость Ua здесь не определяется расчетом, а задается следователем или судом чаще всего на основании показаний свидетелей. Многочисленные опыты, проведенные в разных странах, показали, что при определении скорости автомобиля «на глазок» человек практически всегда ошибается. В одном из экспериментов даже при скорости 30 км/ч три четверти наблюдателей не могли назвать ее точно. Когда же автомобили двигались со скоростью 70 км/ч, большинство было уверено, что скорость составляет 60 или даже 50 км/ч. Поэтому в тех случаях, когда водитель перед наездом на пешехода не тормозил, в материалах уголовного дела можно встретить самые различные показания о скорости Ua.
Для анализа второго условия безопасности преобразуем формулу (5.43):

Мы видим, что с уменьшением j, т. е. при выборе наименьшего значения цх и наибольшего Кэ, получается ответ, более благоприятный для водителя, совершившего наезд на пешехода. Эксперт приходит к благоприятному для водителя выводу и в тех случаях, когда достаточно велики были скорости пешехода или автомобиля, а также мал путь Sп.
Пример 1. Автомобиль, двигавшийся по сухому асфальтобетону с постоянной скоростью 15 м/с, сбил передней частью пешехода, успевшего до наезда пройти по проезжей части 3, 9 м. T1=0, 95 с.
Имел ли водитель техническую возможность предотвратить наезд путем экстренного торможения автомобиля?
Решения. I. Пусть скорость пешехода 2, 0 м/с, а минимальное значение ускорения 7, 0 м/с2, тогда:
время движения пешехода в поле зрения водителя tп=3, 9/2= 1.95 с;
расстояние от автомобиля до места наезда в начальный момент Sуд= 15* 1, 95=29, 3 м;
остановочный путь автомобиля So = 0, 95*15+ 225/(2*7, 0) =30, 4 м.
Условие остановки автомобиля при Sуд==29, 3 м и So=30, 4 м, очевидно, не выполнено. Водитель даже при своевременном торможении не мог бы избежать наезда.
II. При той же скорости пешехода увеличим замедление до 8, 0 м/с2, тогда остановочный путь Sо = 0, 95*15+225/(2*8, 0) =28, 3 м.
Остановочный путь автомобиля (28, 3 м) получился меньше удаления автомобиля от места наезда на пешехода (29, 3 м). Эксперт имеет основания для вывода о том, что у водителя имелась техническая возможность избежать наезда на пешехода, однако он ее не использовал.
III. При повышении скорости движения пешехода, скажем, до 2, 5 м время движения его в поле зрения водителя уменьшится до 1, 44 с, а расстояние до места наезда в момент появления пешехода сократится до 21, 6 м.
Время tп= 3, 6/2, 5 = 1, 44 с. Удаление автомобиля от места наезда Sуд=1, 44*15=21, 6 м< So=28, 3 м, т. е. водитель не располагал технической возможностью избежать наезда. Следовательно, увеличение скорости способствует получению благоприятного для водителя вывода.
Третье условие безопасности выражено так же: S'п  у+ Bа+
у+ Bа+  б, сохраняют силу и формулы для определения S'п, однако выражение для пути S'пн в данном случае должно быть заменено следующим:
б, сохраняют силу и формулы для определения S'п, однако выражение для пути S'пн в данном случае должно быть заменено следующим:
S'пн =So-Syд=Ua(T+ Ua/(2j)-Sп/Uп).
Преобразовав неравенство S'п< ( y+ Bа+
y+ Bа+  б) с учетом перечисленных выражений, получим
б) с учетом перечисленных выражений, получим
 (5.44)
(5.44)
Как свидетельствует последнее выражение, более благоприятные для водителя выводы можно получить, вводя в расчет меньшие значения замедления и большие значения скорости автомобиля.
Пример 2. Определить, имел ли водитель возможность пропустить пешехода при экстренном торможении на сухом асфальтобетоне, если скорость автомобиля Ua во время ДТП была постоянной и составляла
Таблица 5.5. Влияние отдельных параметров на вывод, благоприятный для водителя при наезде в процессе равномерного движения
| Условия безопасности | j | 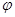 x x
| Kэ | Uп | Sп | Ua |
| 0 | 0 | + | - | 0 | ||
| — | — | + | + | — | + | |
| — | — | + | + | — | + |
14 м/с, путь пешехода до наезда 3, 6 м, расстояние ( y+ Ba+
y+ Ba+  б)= 4, 5 м, скорость пешехода 2 м/с.
б)= 4, 5 м, скорость пешехода 2 м/с.
Решения. I. Пусть замедление равно 7 м/с2, тогда:
расстояние от автомобиля до места наезда в момент возникновения опасности Sуд= 14*3, 6/2, 0=25, 2 м;
остановочный путь автомобиля So=0, 95* 14+196/(2*7)=27, 3 м;
автомобиль, миновав линию следования пешехода, продвинулся бы еще примерно на 2, 1 м (So—Sуд= 27, 3—25, 2=2, 1 м);
скорость автомобиля в момент пересечения линии следования пешехода U'н=  =5, 48 м/с;
=5, 48 м/с;
время движения автомобиля t'дн= 0, 95 +(14— 5, 48) /7, 0 =2, 17 с;
перемещение пешехода S'п= 2, 17*2, 0 =4, 34 м.
Поскольку S'п=4, 34 м< ( y+Bа+
y+Bа+  б)=4, 5 м, пешеход не успел бы уйти с полосы движения автомобиля. Следовательно, при указанных исходных данных получаем вывод, благоприятный для водителя.
б)=4, 5 м, пешеход не успел бы уйти с полосы движения автомобиля. Следовательно, при указанных исходных данных получаем вывод, благоприятный для водителя.
Повторим расчеты, увеличив замедление автомобиля, например, до 8 м/с2 и сохранив остальные исходные данные неизменными. Получаем при своевременном реагировании водителя на возникновение опасной обстановки путь пешехода равным 4, 8 м, что превышает 4, 5 м. Следовательно, пешеход успел бы покинуть пределы опасной зоны, если бы водитель своевременно применил экстренное торможение. Другими словами, вводя в расчет меньшее значение замедления, можно прийти к положительному с точки зрения водителя выводу.
К аналогичным результатам приходим, выбрав большие значения скорости автомобиля Uа и скорости пешехода Un.
Как показывает формула (5.44), при увеличении пути пешехода Sп правая часть неравенства уменьшается, что отрицательно сказывается на выводах. Следовательно, более благоприятное заключение для водителя получим при меньших значениях Sп. Результаты анализа иллюстрирует табл. 5.5.
Сравнение табл. 5.4 и 5.5 показывает, что изменение отдельных параметров в ту или другую сторону сказывается на результатах расчета за небольшими исключениями одинаково независимо от режима движения.