Закон Гука при сдвиге

,

где G – модуль упругости при сдвиге, Н/мм²;

γ – угол сдвига, рад.

Напряжение в любой точке поперечного сечения.

Рассмотрим поперечное сечение круглого бруса.

Под действием внешнего момента в каждой точке поперечного сечения возникают силы упругости dQ:

,

где τ – касательное напряжение;

dA – элементарная площадка.

Т.к. сечение симметрично, то силы dQ образуют пары. Элементарный момент силы dQ относительно центра круга:

,

где ρ – расстояние от точки до центра круга.

Суммарный момент сил упругости (M_к) получается сложением (интегрированием) элементарных моментов:

.

После преобразования, напряжения в точке поперечного сечения:

, где .

При ρ =0 τ _к =0 – касательные напряжения при кручении пропорциональны расстоянию от точки до центра сечения. I_р – полярный момент инерции сечения – характеризует сопротивление сечения скручиванию. Слои расположенные дальше от центра испытывают большие напряжения.

Эпюра распределения касательных напряжений при кручении:

M_к – крутящий момент в сечении; ρ _B – расстояние от точки B до центра; τ _B – напряжение в точке B; – максимальное напряжение.

Максимальные напряжения при кручении.

Касательные напряжения возникают на поверхности.

Максимальное напряжение (ρ _max=d/2, где d – диаметр бруса круглого сечения) на поверхности:

Момент сопротивления при кручении (или полярный момент сопротивления сечения):

.

Таким образом,

.

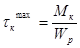Для круглого сечения: .

Для кольцевого сечения: 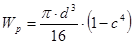, где .

Условие прочности при кручении.

Разрушение бруса при кручении происходит с поверхности, а при расчете на прочность используют условие прочности:

,

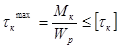где – допускаемое напряжение кручения.