
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача линейного программирования
|
|
1.1. Постановка задачи
Линейное программирование (ЛП) – область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т. е. линейных равенств или неравенств, связывающих эти переменные.
К задачам линейного программирования сводится широкий круг вопросов планирования экономических процессов, где ставится задача поиска наилучшего (оптимального) решения.
Общая задача линейного программирования (ЗЛП) состоит в нахождении экстремального значения (максимума или минимума) линейной функции.
Примером решения задачи является разработка оптимального плана ремонта грузового автотранспорта.
В настоящее время этот вид ремонта выполняется в ремонтных боксах гаражей автотранспортных предприятий.
С учетом того, что в настоящее время неуклонно возрастает парк автотранспорта у различных собственников, возникает проблема определения оптимальной производственной программы депо, обеспечивающей максимальную прибыль предприятию.
Такая задача может быть сформулирована следующим образом. Имеем:
хj – объем ремонта автотранспорта j-го типа; j = 1, 2, … n;
bi – объем, имеющихся в наличии производственных ресурсов i-го вида; i = 1, 2, … m;
aij – расход i-го вида ресурсов на ремонт одной единицы подвижного состава j-го типа;
Cj – прибыль, получаемая предприятием за одну единицы подвижного состава j-го типа.
Решение задачи осуществляется на основе следующей экономико-математической модели.
Найти совокупность переменных хj, максимизирующих целевую функцию F:
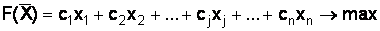 , (1.1)
, (1.1)
при наложенных ограничениях (система m линейных уравнений и неравенств с n переменными):
 , (1.2)
, (1.2)
xj, j = 1….n, (1.3)
где aij, bi, сj – заданные постоянные величины
Линейную функцию (1.1), для которой ищется экстремальное значение, принято называть целевой функцией. Условия (1.2) называются функциональными, а (1.3) – прямыми ограничениями задачи.
Виды задач ЛП:
1) задача оптимального распределения ресурсов при планировании выпуска продукции на предприятии (задача об ассортименте);
2) задача на максимум выпуска продукции при заданном ассортименте;
3) задача о смесях (рационе, диете);
4) транспортная задача;
5) задача о рациональном использовании имеющихся мощностей;
6) задача о назначениях.
Для решения ЗЛП необходимо построить экономико-математическую модель исследуемого экономического процесса.
1.2. Решение задач линейного программирования с помощью надстройки MS Excel «Поиск решения»
Рассматриваемая модель относится к классу экономико-математических моделей линейного программирования.
Решение задач, описываемых экономико-математическими моделями линейного программирования, как правило, осуществляется универсальным симплексным методом.
Он достаточно трудоемок. Поэтому выполнение расчетов рекомендуется в среде MS Excel.
Технологию решения задач линейного программирования в среде MS Excel продемонстрируем на следующем примере.
Вагоноремонтное депо имеет в своем распоряжении определенное количество ресурсов: рабочую силу, материалы, запасные части, оборудование, производственные площади и т. п.
Допустим, например, имеются ресурсы четырех видов: рабочая сила, материалы, специальные запасные части и фонд времени ремонтных позиций.
Гараж может ремонтировать автотранспорт четырех типов. Информация о количестве единиц каждого ресурса, необходимого для ремонта одной подвижной единицы каждого типа, их объеме и получаемой прибыли приведена в табл. 1.1.
Таблица 1.1 - Исходные данные
| Ресурсы | Нормы расхода ресурсов | Наличие ресурсов | |||
| бортовой | крытый фургон | рефриже-ратор | фура | ||
| Раб. сила, чел.-ч | 650 000 | ||||
| Материалы, тыс. руб. | 100 000 | ||||
| Фонд времени, ч | 125 000 | ||||
| Специальные запчасти, тыс. руб. | |||||
| Прибыль на 1 единицу, тыс. руб. | 7, 3 | 7, 5 | 6, 5 |
Требуется найти такой план ремонта вагонов, при котором будет максимальной общая прибыль предприятия.
Обозначим через х1, х2, х3, х4 количество вагонов каждого типа. Сформулируем экономико-математическую модель задачи:
F = 7, 3х1 + 7, 5х2 + 6, 5х3 + 15х4 à max;
180х1 + 205х2 + 160х3 + 336х4 ≤ 650 000;
28х1 + 27x2 + 26х3 + 54х4 ≤ 100 000;
17х1 + 18х2 + 16х3 + 30х 4 ≤ 125 000; (1.4)
15 ∙ х4 ≤ 5000;
x1 ≥ 0; x2 ≥ 0; x3 ≥ 0; x4 ≥ 0.
Решение задач линейного программирования в среде MS Excel осуществляется с помощью надстройки «Поиск решения». Если в меню Сервис отсутствует команда Поиск решения, значит, необходимо загрузить эту надстройку. Выберите команду Сервиса Надстройки и активизируйте надстройку «Поиск решения». Если же этой надстройки нет в диалоговом окне «Надстройки», то необходимо обратиться к панели управления Windows, щелкнуть на пиктограмме Установка и удаление программ и с помощью программы установки MS Excel (или Office) установить надстройку «Поиск решения». Для решения задачи необходимо:
1) создать форму для ввода условий задачи;
2) указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки);
3) ввести исходные данные;
4) ввести зависимость для целевой функции;
5) ввести зависимости для ограничений;
6) указать назначение целевой функции (установить целевую ячейку);
7) ввести ограничения;
8) ввести параметры для решения задачи линейного программирования.
Для рассматриваемого примера продемонстрируем технологию решения задачи оптимального использования ресурсов.
1. Подготовим форму для ввода условий задачи (рис. 1.1).
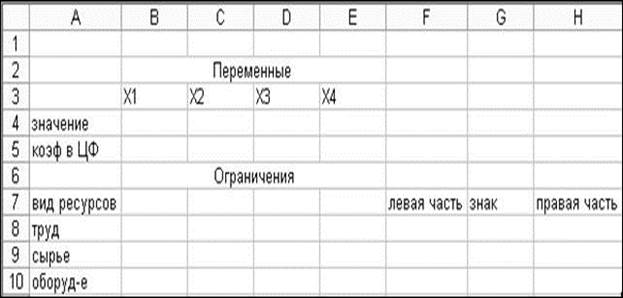
Рисунок 1.1- Форма для ввода условий задачи
2. В задаче оптимальные значения вектора X = (х1, х2 х3, х4) будут помещены в ячейках ВЗ: ЕЗ, оптимальное значение целевой функции – в ячейке F4.
3. Введем исходные данные в созданную форму. Получим результат, показанный на рис. 1.2.
| Переменные | |||||||
| Х1 | Х2 | Х3 | Х4 | ||||
| Значение | ЦФ | ||||||
| коэф. в ЦФ | 7, 3 | 7, 5 | 6, 5 | ||||
| Ограничения | |||||||
| Вид ресурсов | Левая часть | Знак | Правая часть | ||||
| Труд | < = | 650 000 | |||||
| Материалы | < = | 100 000 | |||||
| Фонд времени | < = | 125 000 | |||||
| Спец. запчасти | < = |
Рисунок 1.2- Введённые данные
4. Введем зависимость для целевой функции.
• Курсор в F4.
• Курсор на кнопку Мастер функций.
M1 (Обозначим через М1 следующее действие – «один щелчок левой кнопкой мыши»). На экране диалоговое окно Мастер функций шаг 1 из 2.
• Курсор в окно Категория на категорию Математические.
• M1.
• Курсор в окно Функции на СУММПРОИЗВ.
• M1.
• В массив 1 ввести В$3: Е$3.
• В массив 2 ввести В4: Е4.
• Готово. На экране: в F4 введена функция, как показано на рис. 1.3.


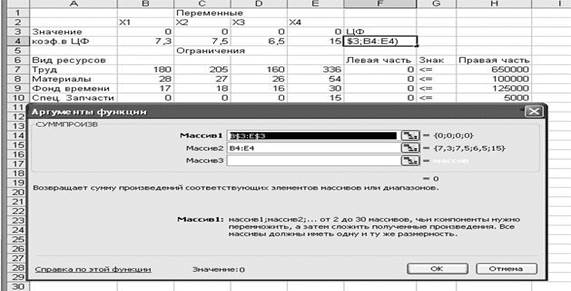
Рисунок 1.3- Вычисление целевой функции
5. Введем зависимость для левых частей ограничений.
• Курсор в F4.
• Копировать в буфер.
• Курсор в F7.
• Вставить из буфера.
• Курсор в F8.
• Вставить из буфера.
• Курсор в F9.
• Вставить из буфера.
На этом ввод зависимостей закончен.
Запуск «Поиска решения».После выбора команд Сервис => Поиск решения появится диалоговое окно «Поиск решения» (рис. 1.4).
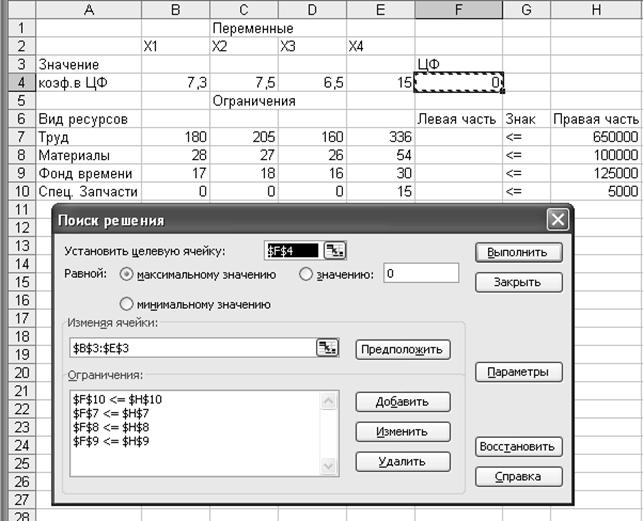
Рисунок 1.4 - Ввод данных в диалоговое окно «Поиск решения»
В диалоговом окне «Поиск решения» есть три основных параметра:
• Установить целевую ячейку.
• Изменяя ячейки.
• Ограничения.
Сначала нужно заполнить поле «Установить целевую ячейку». Во всех задачах для средства Поиск решения оптимизируется результат в одной из ячеек рабочего листа. Целевая ячейка связана с другими ячейками этого рабочего листа с помощью формул. Средство Поиск решения использует формулы, которые дают результат в целевой ячейке, для проверки возможных решений. Можно выбрать поиск наименьшего или наибольшего значения для целевой ячейки или же установить конкретное значение.
Второй важный параметр средства Поиск решения – это параметр. Изменяемые ячейки – это те ячейки, значения в которых будут изменяться для того, чтобы оптимизировать результат в целевой ячейке. Для поиска решения можно указать до 200 изменяемых ячеек. К изменяемым ячейкам предъявляется два основных требования: они не должны содержать формул и изменение их значений должно отражаться на изменении результата в целевой ячейке. Другими словами, целевая ячейка зависима от изменяемых ячеек.
Третий параметр, который нужно вводить для Поиска решения – это Ограничения.
6. Назначение целевой функции (установить целевую ячейку).
• Курсор в поле «Установить целевую ячейку».
• Ввести адрес $F$4.
• Ввести направление целевой функции: Максимальному значению.
• Ввести адреса искомых переменных:
• Курсор в поле «Изменяя ячейки».
• Ввести адреса В$3: Е$3.
7. Ввод ограничений.
• Курсор в поле «Добавить». Появится диалоговое окно «Добавление ограничения» (рис. 1.5).
Рисунок 1.5 - Диалоговое окно «Добавление ограничения»
• В поле «Ссылка на ячейку» ввести адрес $F$7.
• Ввести знак ограничения ≤.
• Курсор в правое окно.
• Ввести адрес $Н$7.
• Добавить. На экране опять диалоговое окно «Добавление ограничения».
• Ввести остальные ограничения.
• После ввода последнего ограничения ввести ОК.
На экране появится диалоговое окно «Поиск решения» с введенными условиями (рис. 1.5).
8. Ввод параметров для решения ЗЛП (рис. 1.6).
• Открыть окно «Параметры поиска решения».
• Установить флажок Линейная модель, что обеспечивает применение симплекс-метода.
• Установить флажок Неотрицательные значения.
• ОК.

Рисунок 1.6 - Параметры «Поиск решения»
Полученное решение (рис. 1.7, 1.8) означает, что максимальную прибыль 26 537, 7 тыс. руб. депо может получить при выпуске из ремонта 2595, 5 бортовых грузовиков, 345, 4 крытых фургонов, 333, 3 фур. При этом ремонт платформ в оптимальном плане производства отсутствует. Ресурсы – рабочее время, материалы, специальные запасные части – будут использованы полностью, а из 125 тыс. ч фонда времени будет использовано только 60, 3 тыс. ч.
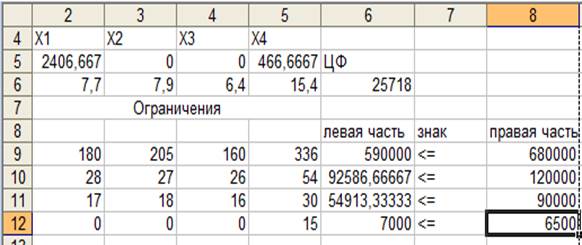
Рисунок 1.7 - Результаты «Поиска решения»
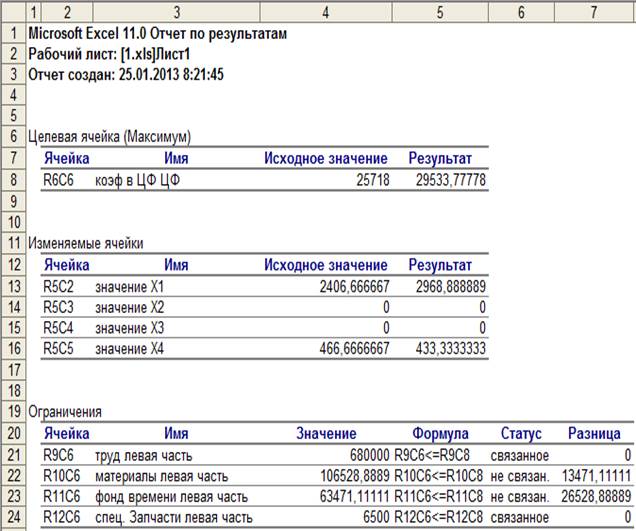
Рисунок 1.8 - Отчет по результатам
MS Excel позволяет представить результаты поиска решения в форме отчета (см. рис. 1.8). Существует три типа таких отчетов.
Результаты (Answer). В отчет включаются исходные и конечные значения целевой и влияющих ячеек, дополнительные сведения об ограничениях.
Устойчивость (Sensitivity). Отчет, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках или в формулах ограничений.
Пределы (Limits). Помимо исходных и конечных значений изменяемых и целевой ячеек в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.
В отчете по результатам содержатся оптимальные значения переменных x1, х2, х3, х4, значение целевой функции, а также левые части ограничений.
В выводе указать (см. рис. 1.7.):
1) максимальную величину прибыли;
2) количество вагонов какого типа следует отремонтировать, чтобы прибыль была максимальной;
3) оценить качество использования ресурсов предприятия.
1.3. Исходные данные
Задача формулируется для вагоноремонтных депо, которые в состоянии ремонтировать пять типов вагонов: полувагоны, крытые, платформы, вагоны-хопперы и цистерны. Предположим, что в производственном процессе используется пять видов ресурсов: рабочая сила, материалы, фонд времени ремонтных позиций, специальные запасные части и электроэнергия. Нормы расхода ресурсов на ремонт одного вагона по типам единые для всех вариантов задания представлены в табл. 1.2.
Таблица 1.2 - Исходные данные
| Ресурсы | Нормы расхода ресурсов на один вагон | ||||
| бортовой | крытый фургон | рефриже-ратор | фура | Цистерна | |
| Раб. сила, чел.-ч | |||||
| Материалы, тыс. руб. | |||||
| Фонд времени, ч | |||||
| Специальные запчасти, тыс. руб. | |||||
| Электроэнергия, тыс. квт∙ ч | 1, 5 | 1, 4 | 0, 9 | 1, 6 | 1, 2 |
Данные о размерах прибыли на 1 отремонтированную единицу подвижного состава и объемах ресурсов на предприятии приведены по вариантам в табл. 1.3 и 1.4.
Таблица 1.3 - Размер прибыли на один отремонтированный вагон
| Номер варианта | Прибыль на 1 единицу, тыс. руб. | ||||
| бортовой | крытый фургон | рефриже-ратор | фура | Цистерна | |
| 7, 3 | 7, 5 | 6, 5 | 15, 0 | 7, 1 | |
| 7, 5 | 7, 7 | 6, 0 | 14, 2 | 7, 3 | |
| 7, 7 | 7, 9 | 6, 4 | 15, 4 | 7, 6 | |
| 8, 0 | 8, 4 | 6, 3 | 15, 7 | 7, 9 | |
| 7, 1 | 8.1 | 7, 0 | 15, 5 | 6, 8 |
Таблица 1.4 - Объемы ресурсов на предприятии
| Номер варианта | Объемы ресурсов | ||||
| Рабочая сила | Материалы | Фонд времени | Специальные запчасти | Электроэнергия | |
| 650 000 | 100 000 | 125 000 | |||
| 590 000 | 98 000 | 80 000 | |||
| 680 000 | 120 000 | 90 000 | |||
| 700 000 | 125 000 | 75 000 | |||
| 750 000 | 130 000 | 88 000 | |||
| 690 000 | 133 000 | 74 000 | |||
| 800 000 | 129 000 | 95 000 | 10 000 | ||
| 790 000 | 130 000 | 80 000 | |||
| 770 000 | 115 000 | 92 000 | |||
| 710 000 | 120 000 | 79 000 |
1.4. Последовательность решения задачи
1. По данным табл. 1.3 и 1.4 определяются номера вариантов исходных данных. Для этого две последние цифры номера зачетной книжки студента делятся с остатком на количество вариантов, представленных в таблицах. К остатку от деления прибавляется единица. Полученное число является номером варианта для информации соответствующего вида.
Например, считываем из зачетной книжки число 89. Норму прибыли на вагон определяем по данным табл. 1.3. Для этого число 89 делим на 5. Получаем 17 и 4 в остатке. Прибавляем к остатку единицу, получаем вариант 5. Если остаток 0, вариант 1. По такой же схеме находим объемы ресурсов.
2. Для соответствующих исходных данных составляется экономико-математическая модель.
3. С использованием надстройки «Поиск решения» пакета EXCEL решается задача с выдачей отчета «Результаты».
4. Полученное решение анализируется, и делаются выводы, в которых дается характеристика найденному оптимальному варианту производственной программы вагоноремонтного предприятия и эффективности использования производственных ресурсов.
2. Элементы теории массового обслуживания
2.1. Постановка задачи
При исследовании операций часто приходится сталкиваться с системами, предназначенными для многоразового использования при решении однотипных задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания (СМО).
Главная особенность процессов массового обслуживания – случайность. При этом имеются две взаимодействующие стороны – обслуживаемая и обслуживающая.
Примерами процессов этого типа являются:
1) обслуживание покупателей в сфере розничной торговли;
2) транспортное обслуживание;
3) медицинское обслуживание населения;
4) ремонт аппаратуры, машин, механизмов, находящихся в эксплуатации;
5) обработка документов в системе управления;
6) туристическое обслуживание.
Неотъемлемой частью системы массового обслуживания является узел обслуживания, через который осуществляется взаимодействие входного и выходного потоков заявок. В случае транспортного обслуживания каналом может считаться отдельная единица транспортного средства.
Вид графической модели зависит как от числа каналов n, так и от допустимой длины очереди m. По указанным признакам различается ряд типов СМО, перечисленных в табл. 2.1.
По числу обслуживающих каналов различают одноканальные и многоканальные СМО.
Находящиеся в СМО заявки могут либо ожидать обслуживания, либо находиться под обслуживанием. Часть заявок, ожидающих обслуживания, образует очередь.
Таблица 2.1 - Типы систем массового обслуживания
| № п/п | Параметры СМО | Тип СМО | |
| n | m | ||
| Одноканальная, без очереди | |||
| n > 1 | Многоканальная, без очереди | ||
| 1 < m < ∞ | Одноканальная, с ограниченной очередью | ||
| n > 1 | 1 < m < ∞ | Многоканальная, с ограниченной очередью | |
| m = ∞ | Одноканальная, с неограниченной очередью | ||
| n > 1 | m = ∞ | Многоканальная, с неограниченной очередью |
В зависимости от целочисленного значения m используются следующие названия в классификации типов СМО:
1) m = 0 – без очереди;
2) m > 0 – с очередью.
Если число мест в очереди m является конечным, то в СМО могут происходить отказы в предоставлении обслуживания некоторым заявкам. В связи с этим СМО указанного типа называются системами с отказами. Отклоняются от обслуживания те заявки, в момент прихода которых все места в очереди случайно оказались занятыми, или, если m = 0, все каналы оказались занятыми. Считается, что заявка, получившая отказ в обслуживании, навсегда теряется для СМО. Таким образом, пропускная способность СМО этого типа всегда меньше 100 %.
Если m не ограничено, что иногда условно записывают как m = 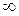 , то соответствующая СМО называется системой с ожиданием. В СМО данного типа пришедшая заявка при отсутствии возможности немедленного обслуживания ожидает обслуживания, какой бы длинной ни были очередь и продолжительность времени ожидания.
, то соответствующая СМО называется системой с ожиданием. В СМО данного типа пришедшая заявка при отсутствии возможности немедленного обслуживания ожидает обслуживания, какой бы длинной ни были очередь и продолжительность времени ожидания.
2.2. Решение задач систем массового обслуживания
Исходные данные приведены в табл. 2.2–2.4.
Некоторые обозначения, применяемые в теории массового обслуживания, для формул:
n – число каналов в СМО;
λ – интенсивность входящего потока заявок Пвх;
v – интенсивность выходящего потока заявок Пвых;
μ – интенсивность потока обслуживания Поб;
ρ – показатель нагрузки системы (трафик);
m – максимальное число мест в очереди, ограничивающее длину очереди заявок;
i – число источников заявок;
pк – вероятность k-го состояния системы;
pо – вероятность простаивания всей системы, т. е. вероятность того, что все каналы свободны;
pсист – вероятность принятия заявки в систему;
pотк – вероятность отказа заявке в принятии ее в систему;
роб – вероятность того, что заявка будет обслужена;
А – абсолютная пропускная способность системы;
Q – относительная пропускная способность системы;
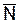 оч – среднее число заявок в очереди;
оч – среднее число заявок в очереди;
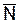 об – среднее число заявок под обслуживанием;
об – среднее число заявок под обслуживанием;
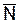 сист – среднее число заявок в системе;
сист – среднее число заявок в системе;
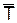 оч – среднее время ожидания заявки в очереди;
оч – среднее время ожидания заявки в очереди;
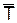 об – среднее время обслуживания заявки, относящееся только к обслуженным заявкам;
об – среднее время обслуживания заявки, относящееся только к обслуженным заявкам;
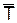 сис – среднее время пребывания заявки в системе;
сис – среднее время пребывания заявки в системе;
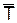 ож – среднее время, ограничивающее ожидание заявки в очереди;
ож – среднее время, ограничивающее ожидание заявки в очереди;
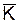 – среднее число занятых каналов.
– среднее число занятых каналов.
Абсолютная пропускная способность СМО А – среднее число заявок, которое может обслужить система за единицу времени.
Относительная пропускная способность СМО Q – отношение среднего числа заявок, обслуживаемых системой в единицу времени, к среднему числу поступающих за это время заявок.
При решении задач массового обслуживания необходимо придерживаться нижеприведенной последовательности:
1) определение типа СМО по табл. 2.1;
2) выбор формул в соответствии с типом СМО;
3) решение задачи;
4) формулирование выводов по задаче.
Вариант выбирается следующим образом: две последние цифры зачетной книжки студента делятся с остатком на количество вариантов, представленных в таблицах. К остатку от деления прибавляется единица. Полученное число явится номером варианта для информации соответствующего вида.
Задача 1. На склад прибывают автопоезда с интенсивностью 0, 9 состава в час. Среднее время обслуживания одного состава 0, 7 часа. Определить показатели эффективности работы склада: интенсивность потока обслуживаний, среднее число заявок в очереди, интенсивность нагрузки канала (трафик), вероятность, что канал свободен, вероятность, что канал занят, среднее число заявок в системе, среднее время пребывания заявки в очереди, среднее время пребывания заявки в системе (табл. 2.2).
Таблица 2.2 - Исходные данные для решения задачи 1
| Показатель | Вариант | |||||||||
| λ | 0, 5 | 0, 8 | 0, 4 | 0, 6 | 0, 7 | 0, 5 | 0, 7 | 0, 6 | 0, 8 | 0, 4 |
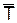 об об
| 0, 3 | 0, 5 | 0, 6 | 0, 9 | 0, 2 | 0, 2 | 0, 4 | 0, 8 | 0, 3 | 0, 5 |
Решение. Склад можно рассматривать как одноканальную СМО с неограниченным ожиданием (т. е. с очередью). Таким образом, параметры системы: число каналов n = 1, число мест в очереди m = 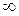 .
.
Интенсивность входящего потока λ = 0, 9 состава в час, среднее время обслуживания одной заявки 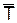 об = 0, 7 ч, интенсивность потока обслуживаний
об = 0, 7 ч, интенсивность потока обслуживаний
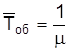 , (2.1)
, (2.1)
μ = 1/0, 7 = 1, 429. Таким образом, нагрузка системы
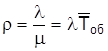 , (2.2)
, (2.2)
ρ = 0, 9/1, 429 = 0, 63, или ρ = 0, 9 ∙ 0, 7 = 0, 63.
Среднее число составов, ожидающих обслуживания,
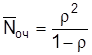 , (2.3)
, (2.3)
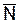 оч = 0, 632/(1 – 0, 63) = 1, 073.
оч = 0, 632/(1 – 0, 63) = 1, 073.
Так как ρ < 1, то очередь автопоездов на разгрузку не может бесконечно возрастать, значит, предельные вероятности существуют. Вероятность того, что станция свободнаp0, рассчитывается по следующей формуле:
pk = ρ k(1 – ρ); k = 0, 1, 2…
p0 =1 – ρ. (2.4)
p0 = 1 – 0, 63 = 0, 37, тогда вероятность того, что станция занята pзан = 1 – – 0, 37 = 0, 63.
Среднее число заявок (составов) в системе рассчитывается по следующей формуле:
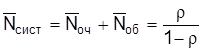 , (2.5)
, (2.5)
где 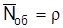 ;
; 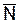 сист = 0, 63/1 – 0, 63 = 1, 703 или
сист = 0, 63/1 – 0, 63 = 1, 703 или 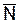 сист = 0, 63 + 1, 073 = 1, 703.
сист = 0, 63 + 1, 073 = 1, 703.
Среднее время пребывания заявки (состава) в очереди (в ожидании обслуживания)
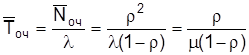 , (2.6)
, (2.6)
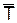 оч = 1, 073/0, 63 = 0, 632/(0, 9(1 – 0, 63)) = 0, 63/(1, 429(1 – 0, 63)) = 1, 19.
оч = 1, 073/0, 63 = 0, 632/(0, 9(1 – 0, 63)) = 0, 63/(1, 429(1 – 0, 63)) = 1, 19.
Среднее время пребывания заявки (состава) в системе (в ожидании обслуживания)
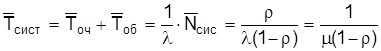 , (2.7)
, (2.7)
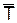 сист = 0, 7 + 1, 19 = 0, 63/(0, 9(1 – 0, 63)) = 1, 703/0, 9 = 1/(1, 429(1 – 0, 63)) = 1, 89.
сист = 0, 7 + 1, 19 = 0, 63/(0, 9(1 – 0, 63)) = 1, 703/0, 9 = 1/(1, 429(1 – 0, 63)) = 1, 89.
Вывод. Очевидно, что скорость обслуживания автопоездов на складе невысокая, так как время на ожидание обслуживания (1, 19 ч) превышает время на обслуживание (0, 7 ч). Для повышения эффективности работы необходимо уменьшить время обслуживания одного автопоезда или увеличить число пунктов обслуживания.
Задача 2. Интенсивность потока пассажиров в кассах автомобильно-дорожного вокзала составляет λ = 1, 35 чел. в мин. Средняя продолжительность обслуживания кассиром одного пассажира 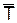 об = 2 мин. Определить минимальное количество кассиров n = nmin, при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при n = nmin (вероятность того, что в узле расчета отсутствуют покупатели, вероятность очереди, среднее число заявок находящихся в очереди, среднее время пребывания заявки в очереди, среднее число заявок, находящихся в системе, среднее время пребывания заявки в системе, доля занятых обслуживанием кассиров, абсолютная пропускную способность) (табл. 2.3).
об = 2 мин. Определить минимальное количество кассиров n = nmin, при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при n = nmin (вероятность того, что в узле расчета отсутствуют покупатели, вероятность очереди, среднее число заявок находящихся в очереди, среднее время пребывания заявки в очереди, среднее число заявок, находящихся в системе, среднее время пребывания заявки в системе, доля занятых обслуживанием кассиров, абсолютная пропускную способность) (табл. 2.3).
Таблица 2.3 - Исходные данные для решения задачи 2
| Показатель | Вариант | |||||||||
| λ | 1, 37 | 1, 62 | 1, 42 | 1, 83 | 1, 75 | 1, 55 | 1, 4 | 1, 65 | 1, 7 | 1, 3 |
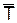 об об
| 2, 3 | 2, 5 | 1, 5 | 1, 7 | 1, 2 | 2, 6 | 2, 5 |
Указание. Прежде чем использовать формулы предельных вероятностей, необходимо быть уверенным в их существовании, ведь в случае, когда время t → 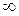 , очередь может неограниченно возрастать. Доказано, что если ρ < 1, т. е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если ρ ≥ 1, очередь растет до бесконечности. Очередь не будет возрастать до бесконечности при условии ρ /n < 1, т. е. при n > ρ.
, очередь может неограниченно возрастать. Доказано, что если ρ < 1, т. е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если ρ ≥ 1, очередь растет до бесконечности. Очередь не будет возрастать до бесконечности при условии ρ /n < 1, т. е. при n > ρ.
Решение. n > 1, m = 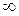 , т. е. имеем многоканальную систему с неограниченной очередью. По условию λ = 1, 35 (1/мин). Показатель нагрузки системы определяется по формуле (2.2): ρ = 1, 35∙ 2 = 2, 7.
, т. е. имеем многоканальную систему с неограниченной очередью. По условию λ = 1, 35 (1/мин). Показатель нагрузки системы определяется по формуле (2.2): ρ = 1, 35∙ 2 = 2, 7.
Очередь не будет возрастать до бесконечности при условии ρ / n < 1, т. е. при n > ρ = 2, 7. Таким образом, минимальное количество контролеров-кассиров nmin = 3.
Найдем характеристики обслуживания СМО при nmin = 3.
Вероятность того, что в узле расчета отсутствуют покупатели, определяется по формуле
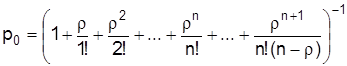 , (2.8)
, (2.8)
р0 = (1 + 2, 7 + 2, 72/2! + 2, 73/3! + 2, 74/3! ∙ (3 – 2, 7))–1 = 0, 025, т. е. в среднем 2, 5 % времени контролеры-кассиры будут простаивать.
Вероятность того, что в узле расчета будет очередь, определяется по формуле
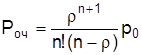 , (2.9)
, (2.9)
Роч = (2, 74/3! (3 – 2, 7)) ∙ 0, 025 = 0, 735.
Среднее число покупателей, находящихся в очереди, определяется по формуле
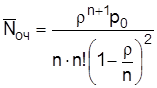 , (2.10)
, (2.10)
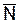 оч = (2, 74/3 ∙ 3! (1 – 2, 7/3)2) ∙ 0, 025 = 7, 35.
оч = (2, 74/3 ∙ 3! (1 – 2, 7/3)2) ∙ 0, 025 = 7, 35.
Среднее время ожидания в очереди определяется по формуле
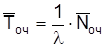 , (2.11)
, (2.11)
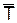 оч = 7, 35/1, 35 = 5, 44 мин.
оч = 7, 35/1, 35 = 5, 44 мин.
Среднее число покупателей в узле расчета определяется по формуле
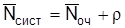 , (2.12)
, (2.12)
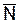 сист = 7, 35 + 2, 7 = 10, 05.
сист = 7, 35 + 2, 7 = 10, 05.
Среднее время нахождения покупателей в узле расчета определяется по формуле
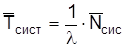 , (2.13)
, (2.13)
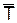 сис = 10, 05/1, 35 = 7, 44 мин.
сис = 10, 05/1, 35 = 7, 44 мин.
Среднее число контролеров-кассиров, занятых обслуживанием покупателей, определяется по формуле
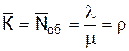 , (2.14)
, (2.14)
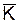 = 2, 7.
= 2, 7.
Коэффициент (доля) занятых обслуживанием контролеров-кассиров
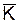 = ρ /n = 2, 7/3 = 0, 9.
= ρ /n = 2, 7/3 = 0, 9.
Абсолютная пропускная способность узла расчета А = 1, 35 (1/мин), или 81 (1/ч), т. е. 81 покупатель в час.
Вывод. Анализ характеристик обслуживания свидетельствует о значительной перегрузке узла расчета при наличии трех кассиров.
Задача 3. На грузовом складе имеется два выгрузочных фронта. Интенсивность подхода составов под выгрузку составляет 0, 4 состава в час. Среднее время разгрузки одного состава – 2 часа. Приходящий автопоезд отправляется на другую склад, если в очереди на разгрузку стоят более трёх автопоездов. Оценить эффективность работы выгрузочных фронтов грузовой станции: вероятность, что выгрузочные фронты свободны, вероятность, что состав останется без разгрузки, относительную пропускную способность, абсолютную пропускную способность, среднее число поездов, ожидающих разгрузки, среднее число заявок в системе, среднее время пребывания заявки в очереди, среднее время пребывания заявки в системе (табл. 2.4).
Таблица 2.4 - Исходные данные для решения задачи 3
| Показатель | Варианты | |||||||||
| λ | 0, 5 | 0, 9 | 0, 5 | 0, 3 | 0, 6 | 0, 8 | 0, 9 | 0, 4 | 0, 6 | 0, 5 |
 об об
| 1, 5 | 1, 4 | 1, 3 | 1, 2 | 1, 5 | 1, 9 | 1, 4 |
Решение. По условию задачи n = 2, m = 3, т. е. грузовая станция представляет собой многоканальную систему с ограниченной очередью. Интенсивность потока обслуживаний определяется по формуле (2.1):
μ =1/2 = 0, 5.
Интенсивность нагрузки канала (трафик) определяется по формуле (2.2): ρ = 0, 4 ∙ 2 = 0, 8.
Вероятность того, что выгрузочный фронт свободен, определяется по формуле
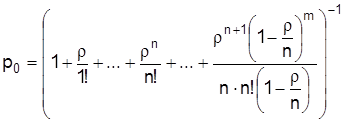 , (2.15)
, (2.15)
р0 = 0, 431.
Вероятность того, что состав будет отправлен на другую склад, определяется по формуле
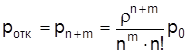 , (2.16)
, (2.16)
ротк = 0, 009.
Относительная пропускная способность определяется по формуле
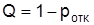 , (2.17)
, (2.17)
Q = 1 – 0, 009 = 0, 991.
Абсолютная пропускная способность определяется по формуле
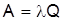 , (2.18)
, (2.18)
А = 0, 4 ∙ 0, 991 = 0, 396, т. е. в среднем в час разгружается 0, 4 состава.
Среднее число составов, ожидающих разгрузки, определяется по формуле
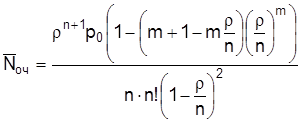 , (2.19)
, (2.19)
где 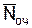 = 0, 21.
= 0, 21.
Среднее время ожидания разгрузки определяется по формуле (2.11): 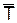 оч = 0, 21/0, 4 = 0, 524.
оч = 0, 21/0, 4 = 0, 524.
Среднее число занятых фронтов (среднее число заявок под обслуживанием) определяется по формуле
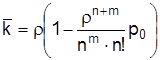 , (2.20)
, (2.20)
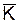 = 0, 77.
= 0, 77.
Среднее число составов, находящихся у разгрузочного фронта определяется по формуле
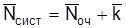 , (2.21)
, (2.21)
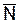 сист = 0, 21 + 0, 77 = 0, 98.
сист = 0, 21 + 0, 77 = 0, 98.
Среднее время пребывания состава у разгрузочного фронта определяется по формуле (2.14):  сис = 1, 564/0, 4 = 3, 908.
сис = 1, 564/0, 4 = 3, 908.
Вывод. Среднее время пребывания состава в ожидании разгрузки на другой станции невелико. Это говорит о нормальной работе выгрузочного узла.
|