Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В-14. Понятие о равноточных и неравноточных измерениях, их обработка
|
|
А) Равноточные измерения
67 Дано: х1 х2 … хn – ряд измерений; n – число измерений Найти: Порядок обработки ряда равноточных измерений:.,, M m x
Решение:
1) Вероятнейшее значение:
Ẍ =[x]/n
2) СКО измеренной величины:
m =√ ошибка ая вероятнейшгде nv m i i
3) СКО вероятнейшего значения:. n m М
по свойству компенсации
68 Вес измерения – условное число, характеристика надежности измерения, степени доверия к нему. 2 i i mc p
где с = Const, m i – СКО i-го измерения. Смысл Const с: с - квадрат СКО такого измерения, вес которого р = 1. - СКО единицы веса: р = 1 с = 2. 2 2 μ i i m p
ВЫВОД: Если известны 2 и mi 2, то можно установить pi - веса измерений, если известны 2 и pi, то можно вычислить mi - СКО измерений. Б) Неравноточные измерения – в процессе измерений хотя бы 1 из 5 факторов изменился
Кольная работа № 1 «Уравнивание равноточных измерений»
1.Задание.
На пункте О измерены углы между направлениями ОА, ОВ, ОС во всех возможных комбинациях. Выполнить оценку углов и дать оценку точности параметрическим способом.
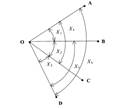
2.Схема.
х4 = х1 + х2
х5 = х2 + х3
х6 = х1 + х2+ х3
3.Исходные данные.
| Градусы (°) | Минуты (') | Секунды (") | Добавка в секунды(") | |
| Х 1 | + | |||
| Х 2 | ||||
| Х 3 | ||||
| Х 4 | ||||
| Х 5 | - | |||
| Х 6 |
4.Условные обозначения параметрических и нормальных уравнений:
Хi – истинное значение измерений;
хi – результаты измерений;
Тi – истинное значение необходимых неизвестных параметров;
t i0 – приближенное значение параметров;
τ i – поправки к ближайшим значениям параметров;
аjk – коэффициенты поправок параметрических уравнений;
li – свободные члены параметрических уравнений;
Njk – коэффициенты нормальных уравнений;
Li – свободные члены нормальных уравнений;
Vi – поправки параметрических уравнений;
xi' – уравненные значения измеренных величин.
В процессе уравнивания принимаем ближайшие значения параметров, находим поправки к ним и вычисляем уравненные значения параметров t i.
Зная параметры поправок находим уравненные значения измеренных величин.
5.Выбор параметров.
Выбираем: Т1=Х1; Т2=Х2; Т3=Х3.
6.Приближенные значения параметров.
ti0 = х1 =
t20= х2 =
t30= х3 =
7.Уравнения связи.
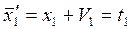
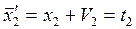
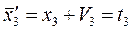(1)
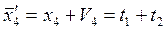
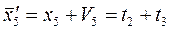
Для определения поправок Vi составляем систему параметрических уравнений в виде:
V1=а11τ 1+а12τ 2+а13τ 3+l1
V2=а21τ 1+а22τ 2+а23τ 3+l2
V3=а31τ 1+а32τ 2+а33τ 3+l3
V4=а41τ 1+а42τ 2+а43τ 3+l4 (2)
V5=а51τ 1+а52τ 2+а53τ 3+l5
V6=а61τ 1+а62τ 2+а63τ 3+l6
Вычисляем коэффициенты аjk и свободные члены системы (2). Находим частные производные уравнений системы (1).
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
.
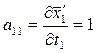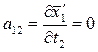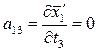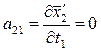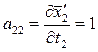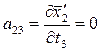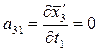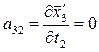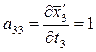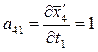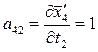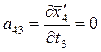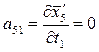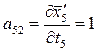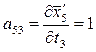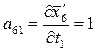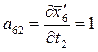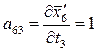Формулы свободных членов уравнений поправок:
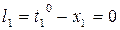
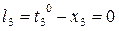
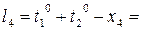
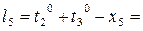
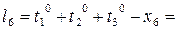
Таблица коэффициентов поправок и нормальных уравнений.
| № п/п | aj1 | aj1 | aj1 | l1 | S1 | V1 |
| Σ | ||||||
| Nj1 | Nj2 | Nj3 | Lj | Σ j | контроль | |
| [ u ], [ lS ] | ||||||
| [ SS ] |
На основании системы уравнений (2) и данных таблицы записываем упрощенное уравнение поправок.
V1 = τ 1 = V2 = τ 2 =V3 = τ 3 =
V4 = τ 1 + τ 2 + l4=
V5 = τ 2 + τ 3 + l5=
V6 = τ 1 + τ 2 + τ 3+ l6=
Для определения τ 1, τ 2, τ 3 составляем систему нормальных уравнений:
N11τ 1 + N12τ 2 + N13τ 3 + L1 = 0
N21τ 1 + N22τ 2 + N23τ 3 + L2 = 0 (3)
N31τ 1 + N32τ 2 + N33τ 3 + L3 = 0
N11 = [ a1a1 ] = a11 a11 + a12 a12 + a13 a13 + a14 a14 + a15 a15 + a16 a16 = 3
N12 = [ a1a2 ] = a11 a12 + a21 a22 + a31 a32 + a41 a42 + a51 a52 + a61 a62 = 2
N13 = [ a1a3 ] = a11 a13 + a21 a23 + a31 a33 + a41 a43 + a51 a53 + a61 a63 = 1
N22 = [ a2a2 ] = a12 a12 + a22 a22 + a23 a23 + a24 a24 + a25 a25 + a26 a26 = 4
N23 = [ a2a3 ] = a12 a12 + a22 a23 + a33 a33 + a42 a43 + a52 a53 + a62 a63 = 2
N33 = [ a3a3 ] = a13 a13 + a23 a23 + a33 a33 + a43 a43 + a53 a53 + a63 a63= 3
L1 = [ a1 l1 ] = a11 l1 + a21 l2 + a31 l4 + a41 l4 + a51 l5 + a61 l6 =
L2 = [ a2 l2 ] = a12 l1 + a22 l2 + a32 l4 + a42 l4 + a52 l5 + a62 l6 =
L3 = [ a3 l3 ] = a13 l1 + a23 l2 + a33 l4 + a43 l4 + a53 l5 + a63 l6 =
После заполнения таблицы выполняем контроль подсчетов, для которого определяют 3 суммы:
Σ 1 = N11 + N12 + N13 + L1 =
Σ 2 = N21 + N22 + N23 + L2 =
Σ 3 = N31 + N32 + N33 + L3 =
Уравнение контроля:
[ SS ] = Σ 1 + Σ 2 + Σ 3 + [ l S ] =
[ l S ] = L1 + L2 + L3 + [ l l ] =
| τ 1 | τ 2 | τ 3 | L | Σ | контроль | ||||||
| Nil | N11 | N12 | N13 | L1 | Σ 1 | ||||||
| Eli | -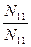 
| - 
| - 
| - 
| - 
| ||||||
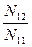
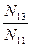
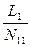
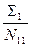
| N2i | N22 | N23 | L2 | Σ 2 | |||||||
| Ni2 Ei2 | N12E12 | N13 E12 | L1 E12 | Σ 1 E12 | |||||||
| 
| 
| 
| 
| |||||||
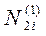
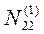
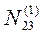
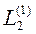
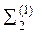
| E2i |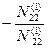 
| 
| 
| 
| |||||||
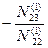
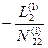
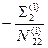
| N3i | N33 | L3 | Σ 3 | ||||||||
| E13 Ni3 | E13N13 | E13L1 | E13 Σ 1 | ||||||||
| 
| 
| 
| ||||||||
| 
| 
| 
| ||||||||
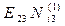
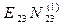
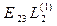
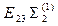
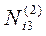
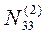
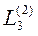
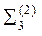
| E3i |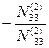 
| 
| 
| ||||||||
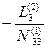
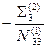
| ll, SS | [ ll ] | [ lS ] | |||||||||
| E 1 l L1 | E 1 l Σ 1 | ||||||||||
| E 1 l L1 | E 1 l Σ 1 | ||||||||||
| 
| ||||||||||
| 
| ||||||||||
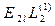
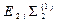
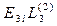
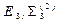
| [ V2 ] = | [ ll] (3) | [ lS ](3) | |||||||||
| τ 3 | E3l | τ 3 = E3l | |||||||||
| τ 2 | τ 2 | E23τ 3 | E2l | τ 2 = E23τ 3 + E2l | |||||||
| τ 1 | τ 1 | E12τ 2 | E13τ 3 | E1l | τ 1 = E12τ 2 + E13τ 3 + E1l |
Контроль:
E11 + E12 + E13 + E1l = E1
E22 + E23 + E2l = E2
E33 + E3l = E3
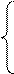
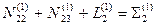
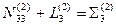
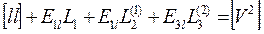
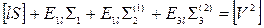
| № угла | Измеренные значения | Vi" | Уравненный угол | Уравнение связи | Контроль |
| |||||
| |||||
| |||||
| |||||
| |||||
|
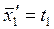
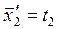
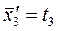
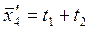
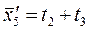
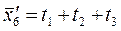
Оценка точности вычислений СКО измеренного угла
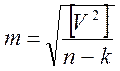
Веса углов х1; х2; х3
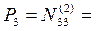
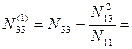
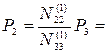
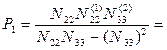
СКО измерения углов:
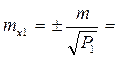
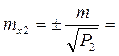
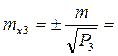
«Уравнивание результатов равноточных измерений коррелатным способом»
Условие: по данным задачи проведем уравновешивание данных и оценим точность результатов измерений.
Выберем функцию трех независимых переменных:
F= x1 + x2 + x3
Составляем систему условных уравнений:
 |
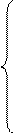x1 + x2 + x3 – х6 =0
(1) x1 + x2 – x4 = 0
х2 + x3 – x5 = 0
Невязки Wi вычисляем из данных задачи:
 |
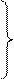W1 = x1 + x2 + x3 – х6
W2 = x1 + x2 – x4 (2)
W3 = х2 + x3 – x5
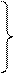Составляем условные уравнения поправок:
a11V1 + a21V2 + a31V3 + a41V4 + a51V5 + a61V6 + W1 = 0
a12V1 + a22V2 + a32V3 + a42V4 + a52V5 + a62V6 + W2 = 0 (3)
a13V1 + a23V2 + a33V3 + a43V4 + a53V5 + a63V6 + W3 = 0
Численные значения Wi вычисляем из (2), коэффициенты уравнений поправок также вычисляем с помощью системы (2) нахождением частных производных:
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
;
; 
; 
.
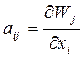
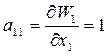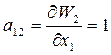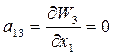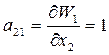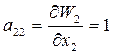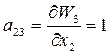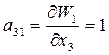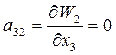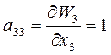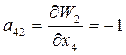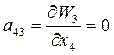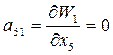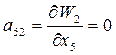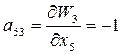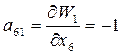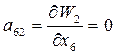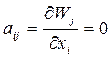Вводя коррелаты k1, k2 k3 – множители Лагранжа – получим выражение для поправок:
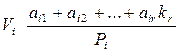(4)
Т.к. измерения равноточные, Рi = 1, r = 3 (число независимых углов).
Для вычисления поправок Vi составляем нормальные уравнения коррелат:
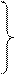
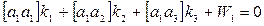
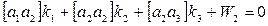(5)
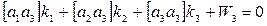
Систему (5) решаем методом Гаусса, определяем k1, k2, k3, а по формуле (4) – поправки Vi.
Для получения коэффициентов систем (3) и (5), составляем таблицы коэффициентов условных и нормальных уравнений.
Таблица коэффициентов условных и нормальных уравнений
| № уравнения | ai1 | ai2 | ai3 | Si' | fi | Σ i | Vi |
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| Σ | Вычисление суммы | ||||||
| Wk | S=S’+W | ||||||
| [ a1 | Sa1= | ||||||
| [ a2 | Sa2= | ||||||
| [ a3 | Sa3= | ||||||
| [ S’ | |||||||
| [ f | |||||||
| [Σ |
Коэффициенты fi вычисляются по формуле: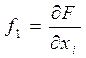 
В соответствии с таблицей записываем системы нормальных уравнений коррелат.
Уравненные значения углов.
| № углов | Измеренные значения | Поправки Vi | Уравненные значения |
Оценка точности:
1) СКО измерений: 
2) Ошибка ошибки: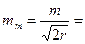 
3) СКО функции F: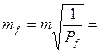 
4) Ошибка самой ошибки: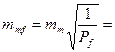 
Контрольная работа № 2 «Уравновешивание неравноточных измерений».
1. Задание.
Выполнить уравнивание параметрическим способом результатов нивелирования. Определить наиболее надежные значения отметок узловых реперов на среднюю квадратическую ошибку нивелирования на один условный километр хода, считая в 1 км 10 станций. Оценку точности уравненных высот I, II, III и разности уравненных отметок HIII – HI провести при помощи весовых коэффициентов.
2. Схема нивелирной сети.
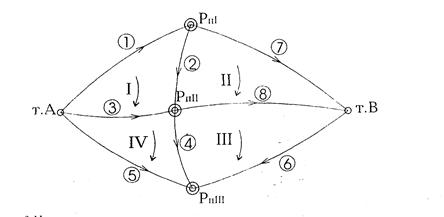
3. Исходные данные.
| № ходов | Превышение h, м | Число станций |
| +1, 953 | 40 «+» | |
| -0, 934 | ||
| +1, 014 | ||
| -0, 406 | ||
| +0, 621 | 45 «-» | |
| -0, 912 | ||
| -0, 417 | ||
| +0, 513 |
Результаты нивелирования по ходам.
Высота опорных марок:
| Марки | Высота Н, м |
| А | 320, 355 |
| В | 321, 897 |
4. Выбор параметров.
В качестве необходимых неизвестных выбираем отметки узловых реперов I, II, III
Т1=Н1; Т1=Н1; Т1=Н1.
5. Приближенные значения параметров.
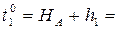
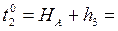
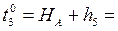
6. Уравнение связи.
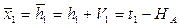
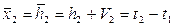
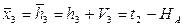
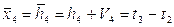
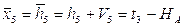
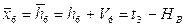
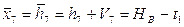
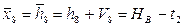
7. Определяем коэффициенты и свободные члены уравнений поправок.
; ; ;
; 
; ;
; 
; 
;
; 
; 
;
; 
; ;
; 
; ;
; 
; 
;
; 
; 
.
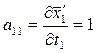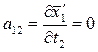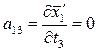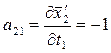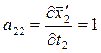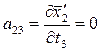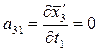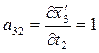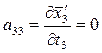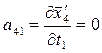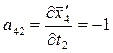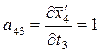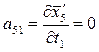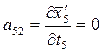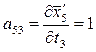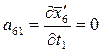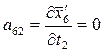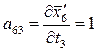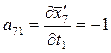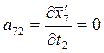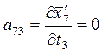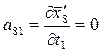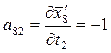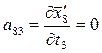Формулы свободных членов:
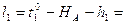
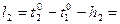
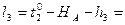
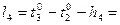
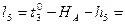
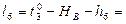
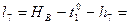
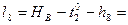
8. Составляем уравнения поправок:
V1 = a11τ 1 + a12τ 2 + a13τ 3 + l1
V2 = a21τ 1 + a22τ 2 + a23τ 3 + l2
V3 = a31τ 1 + a32τ 2 + a33τ 3 + l3
V4 = a41τ 1 + a42τ 2 + a43τ 3 + l4
V5 = a51τ 1 + a52τ 2 + a53τ 3 + l5
V6 = a61τ 1 + a62τ 2 + a63τ 3 + l6
V7 = a71τ 1 + a72τ 2 + a73τ 3 + l7
V8 = a81τ 1 + a82τ 2 + a83τ 3 + l8
Таблица коэффициент уравнений поправок и нормальных уравнений.
| № п/п |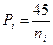 
| ai1 | ai1 | ai1 | li | Si | Vi, см | PiViVi | PiliVi |
| Σ | |||||||||
| Ni1 | Ni2 | Ni3 | Li | Σ i | контроль | ||||
| N1jL1 | [ Pll ] = | ||||||||
| N2jL2 | [ PlS ] = | ||||||||
| N3jL3 | [ PSS ] = |
N11 = [ Pa1a1 ] = P1a11a11 + P2a12a12 + P3a13a13 + P4a14a14 + P5a15a15 + P6a16a16 + P7a17a17 + P8a18a18 =
N12 = [ Pa1a2 ] = P1a11a12 + P2a22a22 + P3a31a32 + P4a41a42 + P5a51a52 + P6a61a62+ P7a71a72 + P8a81a82 =
N13 = [ Pa1a3 ] = P1a11a13 + P2a22a23 + P3a31a33 + P4a41a43 + P5a51a53 + P6a61a63+ P7a71a73 + P8a81a83 =
N22 = [ Pa2a2 ] = P1a12a12 + P2a22a22 + P3a32a32 + P4a42a42 + P5a52a52 + P6a62a62 + P7a72a72 + P8a82a82 =
N232 = [ Pa2a3 ] = P1a12a13 + P2a22a23 + P3a32a33 + P4a42a43 + P5a52a53 + P6a62a63 + P7a72a73 + P8a82a83 =
N33 = [ Pa3a3 ] = P1a13a13 + P2a23a23 + P3a33a33 + P4a43a43 + P5a53a53+ P6a63a63 + P7a73a73+ P8a83a83 =
L1 = = [ Pa1l1 ] = P1a11l1 + P2a21l2 + P3a31l3 + P4a41l4 + P5a51l5 + P6a61l6 + P7a71l7 + P8a81l8 =
L2 = = [ Pa2l2 ] = P1a12l1 + P2a22l2 + P3a32l3 + P4a42l4 + P5a52l5 + P6a62l6 + P7a72l7 + P8a82l8 =
L3 = = [ Pa3l3 ] = P1a13l1 + P2a23l2 + P3a33l3 + P4a43l4 + P5a53l5 + P6a63l6 + P7a73l7 + P8a83l8 =
9.После заполнения таблицы выполняем контроль подсчетов, для которого определяют 3 суммы:
Σ 1= N11 + N12 + N13 + L1 =
Σ 2= N21 + N22 + N23 + L2 =
Σ 3= N31 + N32 + N33 + L3 =
[ PlS ] = L1 + L2 + L3 + [ Pll ] =
[ PSS ] = Σ 1 + Σ 2 + Σ 3 + [ PlS ] =