Теорема о трех последовательностях.

Сохранение знака неравенства для элементов сходящейся последовательности.

Теорема1. Если последовательность сходится к числу a и a< b, то

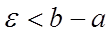Доказательство. Достаточно взять . Тогда, по определению предела, найдется , что для всех , следовательно,

Теорема2. Если последовательность{ } сходится к числу b и b> a, то

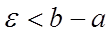Доказательство. Достаточно взять . Тогда, по определению предела, найдется , что для всех , следовательно,

Теорема о переходе к пределу в неравенстве для двух последовательностей.

Теорема3. .Если 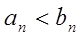для всех n и , то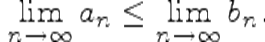
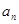Доказательство. Пусть, напротив, . Тогда, в силу теоремы1 начиная с некоторого места все станут меньше , что противоречит условию теоремы.

Замечание. При предельном переходе в неравенстве знак строгого неравенства может перейти в знак нестрогого а в пределе 0=0.

Теорема о трех последовательностях.

Теорема4. Если для всех n и , то Доказательство. Проверим, что выполняется определение сходимости последовательности к числу . Возьмем любое , тогда из условия следует, что 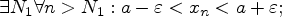из условия следует, что Поэтому для всех выполняются неравенства следовательно, .