Синус, косинус, тангенс, котангенс произвольного угла

Рассмотрим окружность радиуса R с центром в начале декартовой системы координат Oxy.

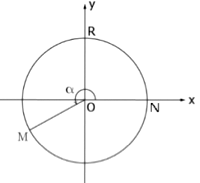
Положительным считается угол NOM, сторона OM которого получена из положительной полуоси Ox в результате поворота, осуществляемого в направлении движения против часовой стрелки.

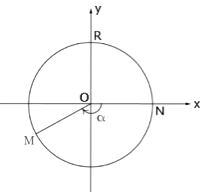
Отрицательным считается угол NOM, сторона OM которого получена из положительной полуоси Ox в результате поворота, осуществляемого в направлении, совпадающем с направлением движения часовой стрелки.

Если для координат точки M ₀ , лежащей на окружности радиуса R с центром в начале координат O,

ввести обозначение

M ₀ = (x ₀ ; y ₀ ),

то, в силу теоремы Пифагора, будет справедливо равенство:

x ₀² + y ₀² = R ²,

и можно сформулировать следующее общее определение тригонометрических функций произвольного угла.

Синусом, косинусом, тангенсом и котангенсом произвольного угла α называют числа, определяемые по формулам:

Как видим, определение тригонометрических функций произвольного угла является естественным обобщением определения тригонометрических функций острого угла.

Чаще всего единичная окружность используется для определения знака тригонометрической функции, числовые значения находятся в таблицах или вычисляются с помощью калькулятора.