Теорема .

Если ряды (1) = и (2) абсолютно сходятся, то их произведение есть тоже абсолютно сходящийся ряд, сумма которого равна произведению сумм сомножителей S= + .

Пример 2. Исследовать ряд на абсолютную или условную сходимость:

а) ; б) ; в) .

Р е ш е н и е.

а) - это знакочередующийся ряд.Проверим выполнение условий признака Лейбница: 1) ; 2) ,

оба условия теоремы выполнены, следовательно, ряд сходится.

Исследуем характер сходимости, для чего составим ряд из абсолютных величин .Получили знакоположительный ряд, гармонический, расходящийся.

Таким образом, знакочередующийся 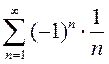ряд сходится, а ряд из абсолютных величин его членов – расходится, следовательно, знакочередующийся ряд - сходится условно.

б)

Ряд знакочередующийся. Проверим выполнение условий признака Лейбница:

1) ; 2) .

Не выполняется необходимое условие сходимости. Следовательно, знакочередующийся ряд - расходится.

в)

Ряд знакочередующийся.Проверим выполнение условий признака Лейбница: 1) 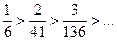; 2) .Оба условия признака Лейбница выполняются, следовательно, знакочередующийся ряд - сходится.

Определим характер сходимости:

Составим ряд из абсолютных величин .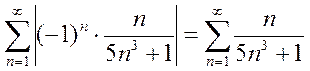

Полученный ряд – знакоположительный, следовательно для определения его сходимости нужно воспользоваться одним из достаточных признаков сходимости знакоположительных рядов.

Воспользуемся признаком сравнения.Сравним ряд с рядом , который сходится.Так как ,

то из сходимости второго ряда следует сходимость первого.

Таким образом, ряд - сходится, а следовательно, знакочередующийся ряд - сходится абсолютно. ¨