Расчет параметров сетевого графика

На рисунке изображен сетевой график, отражающий последовательность выполнения комплекса работ. Известны значения продолжительности t_ij каждой из работ этого графика.

Требуется:

1. Построить сетевой график, нанести на него значения времени выполнения работ.

2. Вычислить ранние и поздние сроки свершения событий и резервы времени событий.

3. Проложить критический путь и указать его продолжительность (если таких путей несколько – указать их все).

4. Вычислить полный и свободный резервы времени работ, не лежащих на критическом пути.

5. Для двух некритических работ вычислить коэффициенты напряженности.

Решение:

Сетевой график комплекса работ

Произведем расчет параметров сетевого графика непосредственно на самом графике. Для этого еще раз изобразим его, разделив каждый из кругов, обозначающих события на 4 сектора. В верхнем секторе указывают номер события, в левом - его ранний срок свершения, в правом - поздний срок, и в нижнем - резерв времени этого события. Вычислим ранние сроки свершения всех событий. Расчет производим в направлении от исходного события к завершающему на основании соотношения .В левом секторе исходного события (события 1) запишем 0. Событию 2 предшествует только одна работа: (1, 2). Ранний срок второго события определяется следующим образом: . Запишем полученное значение в левом секторе второго события. Событию 3 предшествует только работа (1, 3). Ранний срок события 3 будет равен 9: 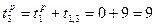.Таким образом рассчитываем для каждого события.

Рисунок 2 - Расчет параметров сетевого графика

Проложим критический путь. Установлено, что события 1, 2, 4, 8, 9 данного сетевого графика не имеют резервов времени. Самым длинным из полных путей, проходящих через эти события является путь 1-2-4-8-9. Его продолжительность T_кр = 8+ 7 + 2 + 8 = 25 временных единиц. На сетевом графике критический путь выделен толстой линией. Таким образом, работы (1, 2), (2, 4),

(4, 8) и (8, 9) являются критическими, т.е. именно от этих работ зависит продолжительность выполнения всего комплекса. При задержке или увеличении продолжительности хотя бы одной из этих работ неизбежно увеличится время выполнения всего комплекса.

В таблице 4.1 приведены характеристики некритических работ , , , , а также полный и свободный резервы времени, вычисленные на основании соотношений:

,

Таблица 4.1 – Резервы времени некритических работ

Работа (i, j)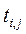
(1, 3)
(3, 4)
(3, 6)
(2, 5)
(2, 7)
(4, 7)
(6, 8)
(5, 7)
(5, 9)
(7, 9)
(8, 9)

Вычислим коэффициенты напряженности работ (1, 2) и (1, 3) на основании соотношения

,

где - продолжительность максимального пути, проходящего через работу (i, j);

- продолжительность отрезка максимального пути, проходящего через работу (i, j), совпадающего с критическим путем;

- длина критического пути.

Максимальный путь, пролегающий через работу (1, 2) имеет вид 1-2-6-9, его продолжительность 19. Этот путь не совпадает с критическим, поэтому = 0. Учитывая, что длина критического пути Т_кр =22, получим

Путь максимальной длины, проходящий через работу (1, 3) - это путь 1-3-4-7-8-9, его продолжительность 21. Этот путь совпадает с критическим на отрезке 4-7-8-9, продолжительность которого = 17. Таким образом, коэффициент напряженности работы

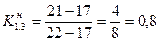
Как видим, коэффициент напряженности работ (1, 3) и (1, 2) достаточно высоки.

Вывод. Произведен расчет параметров сетевого графика. Критический путь пролегает через события 1-2-4-8-9, его продолжительность составляет 25. Критическими являются следующие работы: (1, 2), (2, 4), (4, 8) и (8, 9). Задержка или увеличение продолжительности выполнения хотя бы одной из этих работ приведет к задержке окончания всего комплекса работ. Резервы времени некритических работ приведены в таблице 4.1.