Регрессионный анализ результатов моделирования

Регрессионный анализ – раздел математической статистики, объединяющий методы исследования по статистическим данным зависимости среднего значения одной случайной величины от нескольких других величин 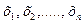. Переменные 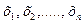являются контролируемыми, не случайными величинами, значения которых задаются при планировании эксперимента. Тогда модель результатов машинного эксперимента графически может быть представлена в виде прямой линии

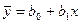(4)

где 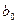– коэффициент ошибок;

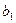– коэффициент регрессии.

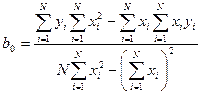, (5)

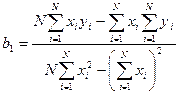, (6)

где N – число измерений при моделировании системы.

Требуется получить такие значения коэффициентов b₀ и b₁, при которых сумма квадратов ошибок модели является минимальной. На рисунке ошибка e_i, 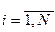, для каждой экспериментальной точки определяется как расстояние по вертикали от этой точки до линии регрессии 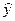=f (х).

Обозначим 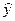_i=b₀+b₁x_i, 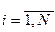. Тогда выражение для ошибок будет иметь вид:

e_i= 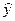_i – y_i=b₀+b₁x_i – y_i, а функция ошибки .

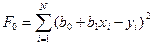Соотношения для вычисления b₀ и b₁ требуют минимального объема памяти ЭВМ для обработки результатов моделирования. Обычно мерой ошибки регрессионной модели служит среднее квадратичное отклонение

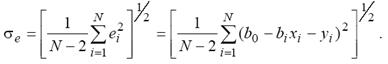
Для нормально распределенных процессов приблизительно 67 % точек находится в пределах одного отклонения σ _e от линии регрессии и 95 % – в пределах 2σ _е (трубки А и B соответственно на рис. 6, б). Для проверки точности оценок b₀ и b₁, в регрессионной модели могут быть использованы, например, критерии Фишера (F -распределение) и Стьюдента (t -распределение). Аналогично могут быть оценены коэффициенты уравнения регрессии и для случая нелинейной аппроксимации.

Регрессионный анализ дает возможность построить модель, наилучшим образом соответствующую набору данных, полученных в ходе машинного эксперимента с системой S. Под наилучшим соответствием понимается минимизированная функция ошибки, являющаяся разностью между прогнозируемой моделью и данными эксперимента. Такой функцией ошибки при регрессионном анализе служит сумма квадратов ошибок.

Пример: Рассмотрим особенности регрессионного анализа результатов моделирования при построении линейной регрессионной модели. На рис. 6, а показаны точки х_i, y_i, 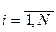, полученные в машинном эксперименте с моделью М системы S. Делаем предположение, что модель результатов машинного эксперимента графически может быть представлена в виде прямой линии

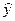=f(x)= b₀+b₁x,

где 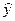– величина, предсказываемая регрессионной моделью.

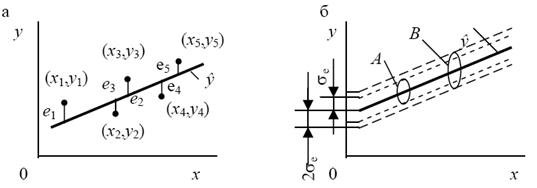
Рис. 6. Построение линейной регрессионной модели.