
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. На стороне AB отложим отрезок AK=CF=BE
|
|
На стороне AB отложим отрезок AK=CF=BE. Из равенства ∆ AKD= ∆ CFD (по двум сторонам и углу между ними) следует, что DK=DF=ED. Углы при основании KE равнобедренного ∆ DKE равны, поэтому равны и смежные им углы AKD и BED. Тогда ∆ AKD =∆ BED( по двум сторонам и углу между ними). Значит, BD=AD=AB, т.е. ∆ ABD – равносторонний. Следовательно,  BAD = 60 o.
BAD = 60 o.
Ответ: 60 o.
[ Задача по геометрии из коллекции задач Р.К. Гордина: Вспомогательные равные треугольники. Правильный (равносторонний) треугольник. Ромбы. Признаки и свойства. ]
№8 Докажите, что если диагонали четырёхугольника делят друг друга пополам, то противоположные стороны четырёхугольника – равны.
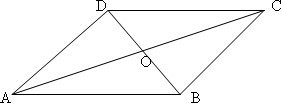 Дано: АВСD – четырёхугольник,
Дано: АВСD – четырёхугольник,
DO=OB, OA=OC.
Доказать: АВ=DC, АD=ВС.
Доказательство:
Для четырехугольника ABCD мы знаем, что AO = OC и BO = OD. Тогда треугольники AOD и BOC также равны (по признаку " сторона-угол-сторона",
AO = OC; BO = OD и углы DOA = BOC – вершина), поэтому AD = BC. Аналогично треугольники AOB и DOC равны, откуда AB = CD.
ч.т.д.
[https://www.matematike.net/geometria/zadachi-na-priznak-ravnosri-treugolnikov-storona-storona-storona.html]
№9 В остроугольном треугольнике ABC высоты AA 1и CC 1пересекаются в точке H. Известно, что H – середина AA 1, а CH: HC 1 = 2: 1. Найдите величину угла АBС.
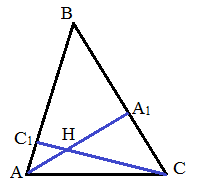
Дано:
 АВС
АВС
AA1 и CC1–высоты
AA1∩ CC1 = Н
H – середина AA1
CH: HC1=2: 1
Найти:  АBС.
АBС.