Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Пусть M – середина отрезка CH
|
|
Пусть M – середина отрезка CH. Тогда треугольники AHC 1и A 1 HM равны по двум сторонам и углу между ними. Поэтому 
A 1 MH= AC 1 H = 90 o.
Отрезок A 1 M – высота и медиана прямоугольного треугольника HA 1 C, значит, этот треугольник равнобедренный. Поэтому C 1 CB = 45 o. Следовательно,
ABC = C 1 CB = 45 o.
Ответ: 45 o.
[ Задача по геометрии из коллекции задач Р.К. Гордина; Вспомогательные равные треугольники. Признаки и свойства равнобедренного треугольника. ]
№10 Доказать, что биссектриса угла есть геометрическое место точек, равноудаленных от его сторон.
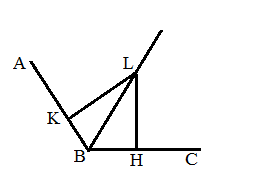
Дано:
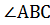, ВL – биссектриса,
LK, LH – перпендикуляры.
Доказать: LK=LH
Доказательство:
Пусть дан произвольный угол АВС, в котором BL – его биссектриса. Докажем, что произвольная точка L биссектрисы равноудалена от его сторон, т. е. LK = LH.
Прямоугольные треугольники BKL и BHL равны по гипотенузе и острому углу, поэтому равны их катеты LK и LH. Поскольку указанным свойством обладают все точки, принадлежащие биссектрисе BF, и не обладает любая точка, ей не принадлежащая, то биссектриса угла и представляет собой указанное геометрическое место точек плоскости.
ч.т.д
[https://www.zadachi.mccme.ru]