
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основы строительной физики
|
|
ДИСЦИПЛИНА «Основы строительной физики» включена в федеральный компонент цикла общих математических и естественно-научных дисциплин основной образовательной программы подготовки по специальности «искусство интерьера». Дисциплина является базовой в системе подготовки выпускников классического университета.
Рабочая программа разработана в соответствии с Государственным образовательным стандартом высшего профессионального образования (ГОС ВПО) по специальности «искусство интерьера». Учтена примерная программа дисциплины, составленная федеральным агентством по образованию Министерства образования и науки Российской федерации.
Функциональное назначение дисциплины – заложить фундамент знаний основных понятий и положений, используемых при проектировании интерьера жилых и общественных помещений.
Курс «основы строительной физики» состоит из следующих разделов:
1. Элементы механики.
2. Элементы теории сопротивления материалов.
3. Элементы климатологии.
4. Основы светологии.
5. Элементы акустики и борьбы с шумами.
Раздел 1. Элементы механики.
1.1. Разделы механики, основные понятия.
Человеческое общество живёт и развивается в материальной среде; человек активно действует на окружающий его мир, состоящий из огромного количества предметов. Тела действуют друг на друга, в результате их взаимодействия происходит изменение взаимного расположения тел – возникает движение, происходящее в пространстве и времени, или изменение формы и размеров – деформирование.
Рассмотрение движения, введение величин его характеризующих, законов, связывающих эти величины, изучение причин, вызывающих движение и законов, связывающих причины и следствие их действия, а также условий, обеспечивающих равновесие тел, и составляет содержание науки, называемой механикой.
Механика содержит три раздела:
Кинематику, изучающую движение, как процесс изменения положения тела без изучения причин его возникновения в пространстве и времени. Вводятся понятия и величины, описывающие этот процесс, а также формулы (законы), связывающие их между собой.
Динамику, изучающую причинно-следственные связи изменений в окружающем мире. Для этого вводятся величины, количественно характеризующие действие тел друг на друга, и их взаимосвязь с величинами, характеризующими результат взаимодействия тел.
Статику, изучающую условия равновесия тел, и законы, обеспечивающие его.
Основные понятия.
Во всех трёх разделах механики есть общие понятия и термины, упрощающие подход к рассмотрению явлений. Первое – наиболее простое – материальная точка. Материальной точкой называют тело, обладающее массой, но не имеющее геометрических размеров. В природе таких тел не существует. Мы будет считать материальной точкой тела, имеющие очень малые размеры, и тела, размерами которых в конкретной задаче можно пренебречь. Одно и то же реальное тело в зависимости от поставленной задачи можно рассматривать либо как материальную точку, либо как тело, размерами которого нельзя пренебрегать.
Любое тело представляет систему материальных точек (реально это атомно-молекулярное строение веществ).
Абсолютно – твёрдое тело – следующая абстрактная модель. Абсолютно – твёрдое тело – неизменяемая система материальных точек при всех внешних воздействиях. Таких тел в природе также не существует, но во многих задачах можно пользоваться этой моделью, если нас не интересует взаимное перемещение частиц тела.
Реальное твёрдое тело характеризуется сохраняемой массой, формой и размерами в нормальных условиях при отсутствии внешнего действия со стороны других тел. При проявлении действия других тел происходят изменения формы, размеров и других параметров исследуемых тел.
Реальные твёрдые тела могут иметь кристаллическую или аморфную структуру. Кристаллические тела имеют разные типы кристаллических решёток, обладают полиморфизмом, чаще всего имеют поликристаллическую структуру, что в свою очередь обеспечивает изотропность свойств поликристаллов в отличие от анизотропности монокристаллов.
В кинематике классической (нерелятивистской) механики мы используем две модели – материальную точку и абсолютно-твёрдое тело.
1.2. Кинематика.
Движением называют процесс изменения с течением времени положения исследуемого тела по отношению к другим телам. С телом (телами), по отношению к которому изучают движение, связывают систему координат. Система координат и способ измерения времени составляют систему отсчёта. Пространство и время, а также процесс движения, являются формой существования материи. Движение никогда и нигде не прекращается, всегда рассматривается относительно какой-либо системы; только условно можно представить абсолютное движение по отношению к условно неподвижной системе отсчёта, в качестве которой чаще всего используют Землю.
При рассмотрении движения тела, знание законов его движения равноценно знанию законов движения всех точек тела.
Начнём с изучения законов движения точки.
Кинематика точки.
Линия, по которой движется точка, называется траекторией (множество последовательных положений движущейся точки). По форме траектории движение может быть прямолинейным и криволинейным.
Описать движение можно двумя способами:
1. Естественным (задается траектория и уравнение движения по ней в виде функции S = f(t), где S – расстояние от начального положения, измеренное вдоль траектории и называемое путём, а t – время от начала движения). Можно соединить начальное положение точки и положение в интересующий нас момент времени направленным отрезком, называемым перемещением.
2. Координатным, при котором движение задается движением проекций исследуемой точки вдоль осей координат (задаются два уравнения x = f(t) и y=f1(t) для плоского движения и три уравнения при движении в пространстве, т.е. добавится функция z = f2(t)). Подставляя время, определим положение проекций точки в любой момент, а тем самым и положение точки А (х, у, z). Можно получить и уравнение траектории, для чего необходимо исключить время.
Разные точки способны двигаться с разной быстротой. Для характеристики быстроты движения вводят величину, называемую скоростью. Если скорость не изменяется во времени, движение называется равномерным; если изменяется – переменным. При равномерном движении по прямой скорость v = S/t и направлена вдоль прямой, по которой движется точка; при переменном и криволинейном движении изменяется величина и направление скорости, что заставляет характеризовать скорость с трех точек зрения: численного значения, направления в пространстве и нахождения точки в пространстве (величины, характеризуемые этими тремя признаками, называют векторными). Таким образом, скорость – векторная величина (имеет численное значение, направление и точку приложения). Направлена скорость в любой точке траектории по касательной к траектории, обозначается буквой v. Для задания численного значения используют два значения:
Среднюю скорость vср = ∆ S/∆ t и мгновенную vмг = lim∆ S/∆ t = dS/dt за бесконечно малый промежуток времени. По смыслу скорость – путь за единицу времени; мгновенная скорость – скорость в данный момент времени. Измеряется скорость в м/с. Скорость – первая производная от пути по времени.
Скорость при движении может изменяться, для характеристики быстроты изменения скорости вводят следующую величину – ускорение a; ускорение также является векторной величиной, используют аср = ∆ v/∆ t и aмг = dv/dt = d2S/dt2.
Истинное (мгновенное) ускорение при прямолинейном движении равно первой производной от скорости или второй производной от пути по времени. Измеряется ускорение в м/с2.
При движении по криволинейной траектории скорость в процессе движения изменяет своё направление, учитывая векторный характер скорости, можно отметить – ускорение также является векторной величиной и направлено в сторону вогнутости кривой и зависит от степени её изогнутости (кривизны). Для упрощения рассмотрения явлений пользуются скалярными величинами, для чего вводят систему координат (чаще всего прямоугольную) и в ней векторные величины заменяют их проекциями на оси координат. При криволинейном движении полное ускорение проецируют не на оси координат, а на нормаль к траектории и касательную к ней: касательная (тангенциальная) составляющая характеризует изменение скорости по величине и равна аt =dv/dt; нормальная составляющая характеризует изменение скорости только по направлению и равна аn =v2/R. При этом полное ускорение а = (аt 2 + an 2)1/2.
В зависимости от составляющих ускорения рассматривают следующие виды движений:
1. an = at = 0 – равномерное прямолинейное (единственное движение без ускорения).
2. аt = const ≠ 0; an = 0 – равнопеременное прямолинейное.
3. at = const ≠ 0; аn ≠ 0 – равнопеременное криволинейное.
4. at = 0; an ≠ 0 – равномерное криволинейное.
5. at ≠ 0; an ≠ 0 – неравномерное криволинейное.
Рассмотрим формулы, описывающие движение: при равномерном движении v = dS/dt = const, что позволяет записать dS = vdt; после интегрирования получаем S – S0 = vt. При начальных условиях S0 = 0 имеем v = const, S = vt.
При равнопеременном движении at = dv/dt = d2S/dt2 = const. Интегрируя первую половину равенства, получим v = v0 + att; т.к. dS = vdt = (v0 + att)dt, интегрирование даёт
S = v0t + att2/2, при равнопеременном движении можно и иначе, а именно S = vсрt = (v + v0)t/2.
Подставляя сюда t = (v – v0)/at, получим S = (v2 –v02)/2at.
По формулам можно построить и графики изменения соответствующих величин, как для равномерного, так и для переменного движения.
Следует обратить внимание на то, что при задании движения в координатной форме, т.е. x = f(t) и y = f1(t) мы получаем vx = dx/dt и vy = dy/dt, что позволит получить v = (vx2 + vy2)1/2. Для ускорения ax = d2x/dt2 и ay = d2 y/dt2a = (ax2 + ay 2)1/2.
Движение твёрдого тела.
В механике рассматривается два вида движений твёрдого тела: поступательное (любая прямая, мысленно проведённая в теле, остается параллельной самой себе; при этом все точки тела движутся по одинаковым траекториям, проходят равные пути, имеют одинаковые скорости и ускорения. Это позволяет описывать поступательное движение твёрдого тела, описывая движение одной его точки) и вращательное (как минимум две точки тела не меняют своего положения в пространстве; остальные, находясь на разном расстоянии от оси вращения, движутся по разным траекториям, с разными скоростями и разными ускорениями. Это означает, что линейное перемещение, линейная скорость и линейное ускорение не могут описать вращательное движение). Положение тела в пространстве при вращательном движении необходимо характеризовать углом поворота тела вокруг оси вращения φ, этот угол зависит от времени φ = f(t), перемещение точки при повороте тела s = rφ, где r – расстояние точки от оси вращения.
Для скорости v = ds/dt = d(rφ)/dt = rdφ /dt = rω, ω = dφ /dt называют угловой скоростью, она характеризует быстроту углового перемещения (измеряют её в рад/сек2).
Итак, s = rφ, v = rω, ω =dφ /dt, at =dv/dt = rdω /dt = rε, ε = dω /dt = d2φ /dt2 .
Классификация вращательных движений будет выглядеть:
1. равномерное вращательное движение ω =const, φ = ω t, at = 0, an =ω 2r=a.
2. неравномерное вращательное движение (угловая скорость изменяется во времени) ε = dω /dt = d2φ /dt2 (измеряется в рад/сек2); at = ε r, an = ω 2 r, a = (at2 + an2)1/2 = ((ε r)2 +(ω 2r)2)1/2 = r (ε 2 + ω 4)1/2.
3. равнопеременное вращательное
ε = dω /dt = const, ω = ε t + ω 0, аналогично
ω = dφ /dt, φ = ω 0 t + ε t2/2.
Однотипность структур формул, описывающих поступательное и вращательное движение, особенно ярко видна в таблице 1:
Таблица 1
| Величина | Характер движения | Поступательное | Вращательное |
| Перемещение | Неравномерное | S = f(t) | φ = f(t) |
| Равномерное | S =vt | φ = ω t | |
| Равнопеременное | S =v0 t +at2 /2 | φ =ω 0t +ε t2 /2 | |
| Скорость | Неравномерное | V = ds/dt | ω = dφ /dt |
| Равномерное | V = const | ω =const | |
| Равнопеременное | V = v0 + at | ω =ω 0 +ε t | |
| Ускорение касательное | Неравномерное | at =dv/dt | ε =dω /dt |
| Равномерное | at = 0 | ε = 0 | |
| Равнопеременное | at = const | ε =const | |
| Ускорение нормальное | an = v2/r | an=ω 2 /r |
1.3. Сложное движение.
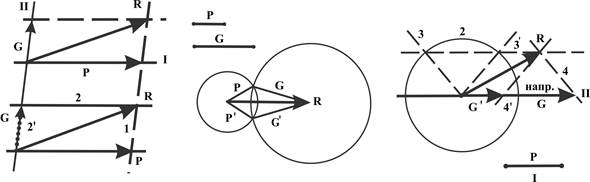
Неподвижных систем координат в природе нет, мы условно принимаем некоторые системы за неподвижные. Реально возникает необходимость рассматривать движение одновременно относительно двух систем – условно неподвижной и движущейся относительно неё, т.е. движение является сложным. Относительно неподвижной системы его называют абсолютным, а относительно движущейся – относительным. Движение системы при этом называют переносным. В итоге: абсолютное движение является сложным и состоит из относительного и переносного. Скорость сложного движения состоит из относительной и переносной скоростей: вектор абсолютной скорости V = Ve + Vr, ve - вектор переносной скорости, Vr – вектор относительной скорости.
1.4. Динамика. Законы динамики.
Динамика изучает движение в зависимости от действия других тел на исследуемое тело. Такое действие характеризуется особой величиной силой (сила – причина, вызывающая движение, причина изменения скорости движения, т.е причина появления ускорения). Измеряется в системе СИ в ньютонах (ньютон – сила, которая телу массой в 1 кг сообщает ускорение 1 м/с2).
Если исследуемая точка не испытывает действия со стороны других тел, она является изолированной (в природе таких тел не существует).
Основные законы динамики:
Первый закон Ньютона (закон инерции). Изолированная материальная точка находится в состоянии покоя или равномерного прямолинейного движения.
Ускорение изолированной материальной точки равно нулю.
Способность материальной точки сохранять ускорение равное нулю называют инертностью или инерцией (иначе говоря – это способность сохранять неизменной по величине и направлению скорость).
Изменить скорость тела можно только действием со стороны других тел, т.е. приложив силу.
Второй закон Ньютона выражает взаимосвязь между приложенной силой и сообщаемым ею ускорением. Ускорение, сообщаемое приложенной силой, пропорционально модулю силы и направлено вдоль действия силы. Р1/Р2 =а1 /а2.
На практике второй закон Ньютона записывают: Р = м а, где м = Р/а = сonst называют массой. [жирными буквами в литературе обозначают вектора].
Чем больше масса, тем большую силу необходимо прилагать для сообщения заданного ускорения. Таким образом, масса – мера инертности тела (одновременно и мера гравитационных свойств тела).
Если учесть, что а = ∆ v/∆ t, можно получить Р = ма = м∆ v/∆ t или Р∆ t = ∆ (mv). Последнее соотношение также часто используют для формулирования второго закона Ньютона: импульс силы, действующей на тело, равен изменению импульса тела (количества движения).
Импульсом силы называют её произведение на время действия Р∆ t, импульсом тела (количеством движения) называют произведение мv.
Следует отметить: под действием постоянной силы тело движется с постоянным ускорением.
К основным законам динамики относят и третий закон Ньютона:
Силы взаимодействия двух тел равны по величине, направлены в противоположные стороны и не уравновешивают друг друга, так как приложены к разным телам.
К основным положениям динамики следует отнести и принцип независимости действия сил: при одновременном действии нескольких сил, ускорение, получаемое телом, равно векторной сумме ускорений, получаемых телом от каждой силы по отдельности.
Используя законы динамики, в механике решаются следующие задачи:
1. по заданному закону движения определяют силы, вызвавшие движение.
2. по известным силам, приложенным к телу, определяют законы движения.
Если тело несвободно, применяется принцип освобождаемости (отбрасываются связи и вместо них вводятся реакции – силы равные связям, но противоположного направления).
1.5. Сложение и разложение сил.
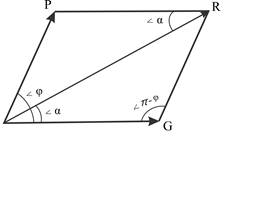 При действии на абсолютно – твёрдое тело двух сил Р и G их можно заменить одной, называемой равнодействующей R, изображаемой диагональю параллелограмма, построенного из составляющих – сторон параллелограмма.
При действии на абсолютно – твёрдое тело двух сил Р и G их можно заменить одной, называемой равнодействующей R, изображаемой диагональю параллелограмма, построенного из составляющих – сторон параллелограмма.
R = P + G, аналитически расчёт проводится с применением теорем косинусов и синусов:
R2 =P2 +G2 +2PG cosφ = P2 +G2 – 2PG cos(π -φ)
P/sinα = R/sin(π -φ) = G/sin(φ -α).
Возможны частные случаи:
φ = 0 даст R = P + G;
φ = 900 даст R2 = (P2 + G2)1/2;
φ = 1800 даст R = P – G.
При рассмотрении обратной задачи – замены одной силы двумя, для получения однозначного ответа необходимы дополнительные условия, т.к. по заданной диагонали параллелограмма построить один параллелограмм невозможно. Возможны варианты дополнительных условий:
1. дополнительно даны направления двух составляющих, определяются их величины.
2. дополнительно даны модуль и направление одной составляющей, определяется модуль и направление второй.
3. дополнительно даны модули обеих составляющих, определяются их направления.
4. дополнительно дан модуль одной составляющей и направление второй, определяется направление первой и модуль второй.
Если рассматривается тело в поле сил земного тяготения, то отдельные частицы тела подвержены действию сил земного тяготения, сумма которых равна весу тела, а точка её приложения, называемая центром тяжести, подлежит определению. Эта точка играет огромную роль при рассмотрении условий равновесия и при рассмотрении поведения тела под действием нескольких внешних сил.
Экспериментально его проще всего определить подвешивая тело дважды в разных точках и после установления равновесия, отмечая вертикальную линию, проходящую через точку подвеса. При равновесии центр тяжести находится на вертикальной линии, проведенной через точку подвеса. Таких линий у нас две, следовательно, центр тяжести находится в точке их пересечения.
1.6. Статика, основные понятия и аксиомы статики.
Статика – раздел теоретической механики, изучающий условия равновесия (покоя или равномерного прямолинейного движения). В статике тело чаще всего рассматривается как абсолютно - твёрдое (его всегда можно представить в виде неизменяемой системы материальных точек).
В статике рассматривают свободные и несвободные (связанные) тела. Большинство тел, окружающих нас, несвободные. Совокупность тел, связанных между собой силами взаимодействия, называют системой. Силы в такой системе – внутренние; тела, не включённые в систему, – внешние и соответствующие им силы – внешние.
В статике всякое тело, при отсутствии действия на него, сохраняет состояние покоя или равномерного прямолинейного движения (аксиома инерции – первый закон Ньютона). На основании третьего закона Ньютона статика утверждает – в природе не существует одностороннего действия (все силы природы – парные). Необходимое и достаточное условие равновесия двух сил – их равенство по величине, действие по одной прямой в противоположном направлении (такие силы называют уравновешенными).
Состояние твёрдого тела не изменится, если к нему приложить или удалить систему уравновешенных сил.
Ограничения положения и скорости движения называют связями. Связи возникают при взаимодействии тел. Действие тела на связь – сила давления, противодействие связи действию тела - сила реакции. Силы подразделяют на активные и реактивные; реактивные зависят от активных.
Несвободное тело можно рассматривать как свободное, для чего необходимо связи заменить их реакциями, направление которых противоположно перемещению уничтожаемому данной связью (так называемый принцип освобождаемости).
Реакции обозначают буквой R. Примеры реакций:
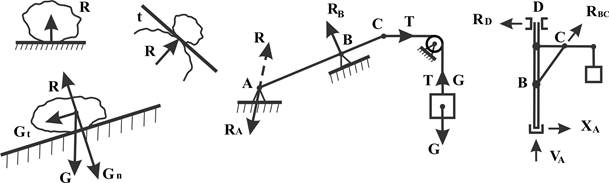
1.7. Момент силы. Главный вектор сил и главный момент системы сил.
При вращательном движении одна и та же сила оказывает разное действие (в отличие от поступательного), действие зависит от места приложения силы. Ещё Леонардо да Винчи (1452 – 1519) ввёл для описания действия силы при вращательном движении понятие момента силы М = РН, Н назвал плечом силы (плечо измеряется по перпендикуляру, проведённому из оси на направление действия силы). Момент считают положительным, если он стремится вызвать вращение против часовой стрелки, и наоборот.
Интерес представляет случай пары сил – системы двух антипараллельных сил равных по величине, лежащих в одной плоскости. Перенос пары не изменяет её момента, пары не имеют равнодействующих, момент пары можно уравновесить только парой, пара не входит ни в уравнение сил, ни в уравнение проекций сил, алгебраическая сумма моментов сил пары относительно любой точки постоянна и равна моменту пары М =Рh, где h – расстояние между силами пары по перпендикуляру к ним.
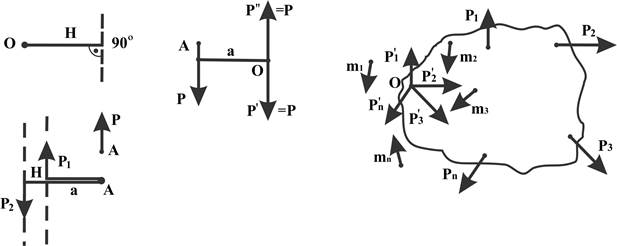 Часто к твёрдому телу приложено несколько сил, действующих в одной плоскости (расположенных произвольно). Механическое состояние твёрдого тела не изменится, если любую силу перенести параллельно самой себе в любую точку тела (называемую точкой приведения или приложения), добавив при этом пару сил, момент которых равен моменту данной силы относительно новой точки приложения.
Часто к твёрдому телу приложено несколько сил, действующих в одной плоскости (расположенных произвольно). Механическое состояние твёрдого тела не изменится, если любую силу перенести параллельно самой себе в любую точку тела (называемую точкой приведения или приложения), добавив при этом пару сил, момент которых равен моменту данной силы относительно новой точки приложения.
В общем случае плоская система произвольно расположенных сил эквивалентна одной силе, приложенной в точке приведения и одной паре. Эта сила называется главным вектором системы (определяют его как равнодействующую сил. перенесённых в точку приведения). Модуль главного вектора R = (Rx2 + Ry2)1/2 = ((∑ X)2 +(∑ Y)2)1/2. Плоская система введённых пар может быть заменена одной эквивалентной парой – главным моментом системы сил: М = m1 + m2 +…+mn = ∑ M0 (Pi).
Главный вектор и главный момент плоской системы произвольно расположенных сил обладают следующими свойствами:
1. модуль и направление главного вектора системы не зависит от положения центра приведения.
2. величина и знак главного момента системы зависят от положения центра приведения (приложения), так как изменение положения центра приведения сопровождается изменением плеч сил.
3. главный вектор и равнодействующая системы сил векторно равны, но не всегда эквивалентны R` = R = ((∑ X)2 + (∑ Y)2)1/2. По главному моменту и равнодействующей сил можно определить плечо равнодействующей d = M/R, которое определит положение линии действия равнодействующей.
Главный вектор и равнодействующая эквивалентны лишь при главном моменте равном нулю, что в свою очередь возможно при расположении центра приведения на линии действия равнодействующей. Сказанное позволило Вариньону (1654 - 1722) сформулировать теорему, носящую его имя, о моменте равнодействующей:
Момент равнодействующей относительно какой-либо точки, расположенной в плоскости действия сил, равен алгебраической сумме моментов составляющих сил относительно той же точки.
Возможные варианты:
1. R = 0, M = 0. Система сил такова, что тело в равновесии.
2. R ≠ 0, M ≠ 0. Модуль равнодействующей равен модулю главного вектора, параллелен ему, но направлен по другой линии.
3. R ≠ 0, M = 0. Линия действия равнодействующей проходит центр приведения и совпадает с главным вектором.
4. R = 0, M ≠ 0. Система эквивалентна паре, у которой величина и знак не зависят от положения центра приведения (одна и та же система сил не может иметь несколько эквивалентных пар).
Для равновесия плоской системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на оси координат равнялась нулю, а алгебраическая сумма моментов этих сил относительно любой точки плоскости также равнялась нулю:
∑ X =0, ∑ Y = 0, ∑ M = 0.