
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Раздел 2. Элементы теории сопротивления материалов.
|
|
2.1. Задачи, решаемые в сопротивлении материалов. Допущения, лежащие в основе.
Сооружения и машины должны обладать:
Прочностью – сопротивляться разрушению (расчёт на прочность – первая задача сопромата).
Жесткостью – сопротивляться деформации (расчёт на жесткость – вторая задача сопромата).
Устойчивостью – сопротивляться отклонению от положения равновесия (расчёт на устойчивость – третья задача сопротивления материалов).
При этом постоянно необходимо заботиться об экономии материалов. Сложные конструкции сводят к простым типам, используя следующие термины:
Брус – тело, у которого 2 размера малы по сравнению с третьим; при прямолинейной оси его называют стержнем.
Пластина – тело ограничено двумя плоскостями, между которыми расстояние мало.
Оболочка – тело ограничено двумя криволинейными поверхностями.
Массив – все три размера тела одного порядка.
Принимаются некоторые упрощения относительно свойств материалов, нагрузок и характера их действия:
Материал считается сплошным (имеющим непрерывное строение).
Материал считается однородным (во всех точках свойства одинаковы).
Материал считается изотропным (свойства одинаковы по всем направлениям).
До приложения нагрузки со стороны других тел в исследуемом теле нет внутренних начальных усилий.
Предполагается независимость действия сил (каждая сила создает свой результат, результат действия нескольких сил суммируется). Предполагается, что перемещение точек приложения сил при деформировании гораздо меньше размеров тела (тела считаются линейно деформируемыми).
В точках достаточно удалённых от места приложения нагрузки величина внутренних сил мало зависит от способа их приложения (принцип Сен-Венана).
2.2. Нагрузки: сосредоточенные и распределённые. Напряжения нормальные и касательные. Виды напряженных состояний.
Исследуемое тело подвергается действию других тел. Для описания действия используют силы, моменты сил. Это действие называется внешним. Силы могут быть сосредоточенными – действующими в точке (в природе таких нет, но их введение упрощает расчёт) и распределёнными по поверхности или объёму (поверхностные и объёмные).
И сосредоточенные, и распределённые нагрузки могут быть статическими (ускорение при этом равно или близко к нулю) и динамическими (ускорение не равно нулю и оно рождает силы инерции). Динамические силы могут иметь установившийся или неустановившийся режим действия.
Расчётную нагрузку определяют, вводя запас прочности, коэффициент запаса прочности определяет во сколько раз достигаемые нагрузки меньше предельных.
Если внешние силы лежат в одной плоскости, вводят продольную силу N, поперечную Q и изгибающий момент Ми. Внешняя нагрузка всегда рождает внутренние силы (силы упругости). Если внешние силы не лежат в одной плоскости, внутренних усилий возникает шесть: N; Qx и Qy (проекции поперечной силы на оси); Мих и Миу (проекции изгибающего момента на оси х и у); Мк = Мz.
В поперечном сечении могут возникать:
1. только продольная сила N (деформация растяжения или сжатия).
2. только Qx или Qy (деформация сдвига).
3. только Мк (деформация кручения).
4. только Мих или Миу (деформация изгиба).
5. несколько усилий – сложная деформация.
Под действием нагрузок происходит деформация – изменение формы и размеров тела. Деформации можно классифицировать по разным признакам:
1. По характеру проведения тела после снятия нагрузок – упругие и пластические (при упругих тело принимает первоначальную форму и размеры, при пластических имеются остаточные деформации). В конструкциях элементы всегда должны испытывать только упругие деформации.
2. По виду происходящих изменений формы – линейные и угловые (линейные – удлинение и укорочение, угловые – изгиб и кручение).
Расчёты удобнее производить, используя величины напряжений, – усилий, приходящихся на единицу площади. Используют нормальные напряжения σ (растягивающее и сжимающее, растягивающее считается положительным) и касательные τ (τ zx и τ zy). Совокупность напряжений называют напряжённым состоянием: если по граням выделенного в материале куба действуют только нормальные напряжения, грани называют главными площадками и напряжения главными σ 1, σ 2, σ 3. Наибольшее обозначают σ 1, наименьшее σ 3. По числу главных напряжений имеем напряжённое состояние: объемное (все три не равны нулю); плоское (два главных напряжения не равны нулю) и линейное (только одно не равно нулю).
Прочность детали оценивают по наибольшему нормальному или касательному напряжению, которое не должно превышать допустимое (такое, которое обеспечивает нормальную эксплуатацию конструкции):
σ мах ≤ [σ ] или τ мах ≤ [τ ].
2.3. Понятие деформации и их классификация.
Деформация – изменение формы и размеров тела под действием приложенных внешних нагрузок. Деформации могут быть разными, но всегда остается неизменным объем деформируемого тела. Объем определяется произведением трёх параметров – длины, ширины и высоты, следовательно, при любом виде деформации изменение одного из этих параметров сопровождается одновременным изменением других. Это необходимо всегда учитывать, даже если ведется речь о простых деформациях, при которых деформация вызывается одним видом сил или моментов. Общую картину можно изобразить на рисунке в пространственной прямоугольной декартовой системе координат (продольную ось всегда в сопромате выбирают 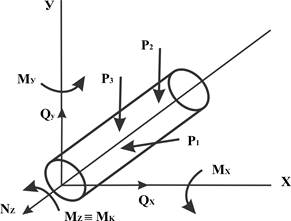 совпадающей с осью Z):
совпадающей с осью Z):
Если существует только продольная сила N - деформация растяжения или сжатия. При наличии одной только поперечной cилы Qx или Qy – сдвиг.
При действии только крутящего момента Мк - кручение. Действие изгибающего момента (одного) Мих или Миу сопровождается изгибом относительно соответствующей оси.
Комбинация перечисленных вариантов приводит к сложной деформации, в которой присутствуют элементы перечисленных простых.
2.4. Закон Гука при растяжении и сжатии. Модуль Юнга.
Если к закреплённому призматическому стержню приложить нормально к торцовому сечению продольную растягивающую силу N, предварительно нанеся на поверхности сетку взаимно перпендикулярных линий, мы увидим: поперечные сечения плоские и нормальные к оси такими и останутся (это означает, что в поперечных сечениях действуют только нормальные напряжения σ = N/F равномерно распределенные по сечению); длина увеличится; поперечные размеры уменьшатся (при сжатии наоборот). Удлинение ∆ l = l – l0 называют абсолютной деформацией; отношение ∆ l/l0 = ε называют относительной деформацией (эта величина показывает на какую долю от первоначальной длины изменяется размер тела при деформировании). До определенных напряжений наблюдается линейный рост относительной деформации с ростом напряжений (это интервал упругих деформаций, которые полностью исчезают при снятии нагрузки), т.е.
ε = σ /Е; σ = Еε или ∆ l/l0 = N/EF – закон Гука при растяжении (сжатии).
Из закона Гука можно найти ∆ l = Nl0/EF или N = EF∆ l/l0 (по приложенной силе и параметрам образца определить абсолютную деформацию или по замеренной деформации и параметрам образца определить усилие, создающее деформацию).
Фигурирующий в формуле коэффициент Е для каждого материала имеет своё значение, характеризует упругие свойства материала при деформациях растяжения (сжатия), носит название модуля Юнга или модуля упругости первого рода. Его всегда можно найти в справочниках для любого материала. Физический смысл легко уяснить, если в закон Гука подставить площадь поперечного сечения равную единице и относительную деформацию взять равной единице; это даст следующий результат |E| = |N| - численное значение модуля Юнга равно продольному усилию, которое действуя на образец с площадью сечения равной единице вызовет относительную деформацию равную единице (при растяжении вызовет удлинение образца в два раза).
При продольной деформации возникает сопутствующая ей поперечная (при удлинении поперечные размеры уменьшаются).
Если ε – продольная деформация, то поперечная ε ' = - μ ε;
μ = - ε '/ε
называют коэффициентом поперечной деформации (коэффициентом Пуассона). Для большинства материалов он имеет значение, лежащее в интервале от нуля до 0, 5 (чаще всего 0, 25 ≤ μ ≤ 0, 35). При расчётах пользуются ещё одним важным коэффициентом – коэффициентом запаса прочности [n] = σ т/[σ ]. При растяжении σ = N/F ≤ [σ ] = σ т/[n] (σ т – предел текучести, [σ ] – предельно допустимое напряжение). Аналогично при касательных напряжениях.
2.5. Плоское нагружение. Обобщённый закон Гука.
Рассмотрим образец с одноосным нагружением σ 1 = N/F и проведём наклонное сечение АВ, расположенное под углом α (угол отсчитываем против часовой стрелки). При поперечном сечении образца F, наклонное сечение равно Fα = F/cosα и в нём действуют нормальное σ α и касательное τ α напряжения. Для нижней части образца запишем условия равновесия (для сил перпендикулярных к АВ и касательных).
σ α Fα – (σ 1 F)cosα = 0 даст σ α = σ 1 cos2α;
τ α Fα – (σ 1F)sinα = 0 даст τ α = (σ 1sin2α)/2 после подстановки вместо F = Fα cosα.
При α = 0 σ α = σ 1 и τ α = 0, т.е. поперечное сечение является главной площадкой, а σ 1- главное напряжение.
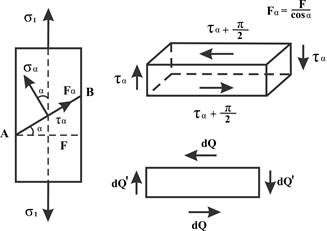 При α = 900 σ α = τ α = 0 – в продольных сечениях нет вообще напряжений.
При α = 900 σ α = τ α = 0 – в продольных сечениях нет вообще напряжений.
При α = 450 σ α = τ α = σ 1/2 растяжение сопровождается появлением линий Людерса – Чернова.
Для сечения перпендикулярного АВ угол будет 900 + α и наши формулы дадут σ α +90 = σ 1sin2α и τ α + 90 = - (σ 1sin2α)/2; получим суммируя σ α + σ α +90 = σ 1; τ α = - τ α +90 (во взаимно перпендикулярных площадках касательные напряжения одинаковы и направлены либо оба к ребру – при сжатии; либо от ребра – при растяжении; можно говорить о законе парности касательных напряжений).
При плоском (двухосном) нагружении - наличии двух нормальных напряжений (по граням действуют только нормальные напряжения) получим:
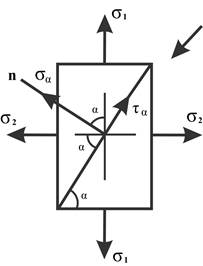 σ α = σ 1cos2α + σ 2cos2(90 – α) = σ 1cos2α +σ 2sin2α;
σ α = σ 1cos2α + σ 2cos2(90 – α) = σ 1cos2α +σ 2sin2α;
τ α = (σ 1sin2α)/2 + (σ 2sin2(90 – α))/2 = (σ 1- σ 2)sin2α /2.
При α = 450 касательное напряжение максимально и равно τ max = (σ 1 – σ 2)/2.
Частные случаи: σ 1 = σ 2 = σ даст σ α = σ и τ α = 0; при σ 1 = σ и σ 2 = - σ имеем чистый сдвиг (α = 450 даёт σ α = 0 и τ α = σ; α = 1350 даёт σ α = 0 и τ α = σ).
Определим деформации в направлении главных напряжений σ 1 и σ 2, применяя закон Гука, и учитывая связь продольных и поперечных деформаций через коэффициент Пуассона μ (коэффициент продольных и поперечных деформаций). Кроме того, воспользуемся принципом независимости действия сил. По вертикали (вдоль направления силы первой) растяжение ε 11 = σ 1/Е от σ 1 и ε 21 = -μ σ 1/Е (сужение в поперечном направлении – вдоль направления второй силы от действия первой); аналогично, растяжение ε 22 = σ 2/Е от σ 2 и ε 12 = -μ σ 2/Е – сужение в вертикальном направлении от действия σ 2.
Суммируем деформации по каждому направлению:
получим ε 1 = ε 11 + ε 12 = σ 1/Е – μ σ 2/Е; ε 2 = ε 22 + ε 21 = σ 2/Е – μ σ 1/Е.
Эти формулы носят название обобщённого закона Гука для плоского напряженного состояния. По деформациям можно определить напряжения:
σ 1 = Е(ε 1 + μ ε 2)/(1 – μ 2) и σ 2 = Е(ε 2 + μ ε 1)/(1 – μ 2).
2.6. Сдвиг. Модуль упругости второго рода. Закон Гука при сдвиге.
Чистый сдвиг – деформация, возникающая при наличии на гранях образца только касательных напряжений. Площадки, по которым действуют только касательные напряжения, называют площадками чистого сдвига. При чистом сдвиге одно главное напряжение - растягивающее, другое – сжимающее; они равны по величине; главные площадки наклонены под 450 к площадкам чистого сдвига. Рассмотрим прямоугольный брус АВСД и 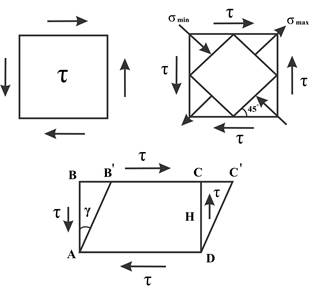 приложим к нему касательные напряжения τ. Брус в сечении примет форму параллелограмма А’B’C’D’, сдвиг грани ВС характеризует относительный сдвиг γ – угол сдвига (угловая деформация). BB’ называют абсолютным сдвигом. Угол γ не зависит от высоты бруса H.
приложим к нему касательные напряжения τ. Брус в сечении примет форму параллелограмма А’B’C’D’, сдвиг грани ВС характеризует относительный сдвиг γ – угол сдвига (угловая деформация). BB’ называют абсолютным сдвигом. Угол γ не зависит от высоты бруса H.
Гуком установлено: до определённых пределов нагружения угол сдвига γ прямо пропорционален касательному напряжению τ, т.е.
γ = τ /G
(сравним с формулой закона Гука при растяжении ε = σ /Е).
Можно записать и иначе: τ = γ G при сдвиге (при растяжении σ = ε Е).
Продолжая аналогию, назвали G – модулем упругости второго рода (модуль сдвига). Он характеризует жёсткость материала – способность материала сопротивляться деформации сдвига. Объёмная деформация равна нулю, связь продольной и поперечной определяется коэффициентом Пуассона μ = ε '/ε, а с учётом направления ε ' = - μ ε. Между Е и G (модулем продольной упругости и модулем сдвига) существует зависимость
G = E/2(1 + μ)
2.7. Кручение. Закон Гука при кручении.
Кручение – деформация, при которой в любом поперечном сечении возникает только крутящий момент (стержни, работающие на кручение, называют валами; обычно валы бывают круглого или кольцевого сечения).
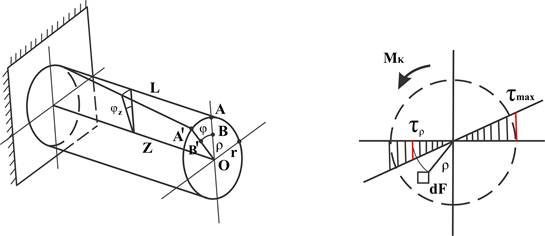 В поперечном сечении действуют непрерывно распределённые внутренние касательные силы. Подвергая кручению резиновый стержень круглого сечения, на котором нанесена сетка из продольных прямых линий и поперечных окружностей мы увидим: ось кручения остаётся прямолинейной; диаметры поперечных сечений и расстояния между ними не изменяются; образующие превращаются в винтовые линии (прямоугольники на боковой поверхности превращаются в параллелограммы) – τ ≠ 0 в продольных и поперечных сечениях; т.к. σ = 0, а τ ≠ 0 – у нас чистый сдвиг; углы поворота поперечных сечений прямо пропорциональны расстоянию от закреплённого сечения.
В поперечном сечении действуют непрерывно распределённые внутренние касательные силы. Подвергая кручению резиновый стержень круглого сечения, на котором нанесена сетка из продольных прямых линий и поперечных окружностей мы увидим: ось кручения остаётся прямолинейной; диаметры поперечных сечений и расстояния между ними не изменяются; образующие превращаются в винтовые линии (прямоугольники на боковой поверхности превращаются в параллелограммы) – τ ≠ 0 в продольных и поперечных сечениях; т.к. σ = 0, а τ ≠ 0 – у нас чистый сдвиг; углы поворота поперечных сечений прямо пропорциональны расстоянию от закреплённого сечения.
Угол φ поворота концевого сечения называется полным углом закручивания цилиндра. Угол закручивания стержня единичной длины φ 0 = φ /l называют относительным углом закручивания (φ 0 = const).
При закручивании сдвиг aa' = r φ; bb' = ρ φ; r = oa; ρ = ob.
Относительный сдвиг γ ρ = ρ φ 0.
По закону Гука для сдвига τ ρ = γ ρ G = ρ φ 0G
При ρ = 0 τ 0 = 0, а при ρ = r τ = τ max= Grφ 0 у поверхности (на наибольшем удалении от оси кручения). Касательные напряжения при кручении прямо пропорциональны расстоянию точек сечения от оси dQ = τ ρ dF,
следовательно Мк = ∫ dQρ = ∫ τ ρ dFρ = ∫ Gρ τ 0dFρ =Gφ 0 ∫ ρ 2dF = Gφ 0Iρ ,
где Iρ = ∫ ρ 2dF – полярный момент инерции вала. Это позволяет записать
φ 0 =Мк/GIρ и φ = φ 0l = Mкl/GIρ ; GIρ – называют жёсткостью при кручении.
Т.к. τ ρ = Gφ 0ρ, a φ 0 = Mk/GIρ выразим τ ρ = Мкρ /Iρ и τ мах = Мкr/Iρ = Mk/Wρ , где Wρ = Iρ /r называют моментом сопротивления кручению.
2.8. Изгиб, поперечная сила, напряжения при изгибе.
Чистый изгиб прямого бруса – деформация, при которой в любом поперечном сечении действует только изгибающий момент. На практике это произойдёт, если к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил.
Рассмотрим брус с одной плоскостью симметрии и совпадающую с ней плоскость действия нагрузок. Деформация произойдёт в плоскости действия внешних сил. Представим балку как множество волокон параллельных оси. Легко проделать опыт с призматическим резиновым брусом прямоугольного поперечного сечения и нанесённой сеткой продольных и поперечных прямых линий:
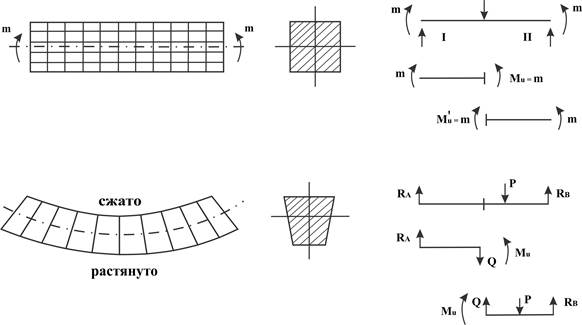
В результате деформирования увидим:
1. Поперечные прямые остаются прямыми.
2. Продольные прямые и ось искривляются.
3. Сечения бруса расширяются в поперечном направлении на вогнутой стороне и сузятся на выпуклой (в поперечных сечениях возникают только нормальные напряжения растяжения и сжатия, неравномерно распределённые по сечению. Эта неравномерность искривляет волокна). Линия пересечения нейтрального слоя с плоскостью симметрии – нейтральная ось (σ = 0).
Наряду с внешними активными силами силы реакции связей определяют внутренние силы.
При решении задач балку принято изображать одной линией – осью и к ней прикладывать активные и реактивные силы; рассмотрим два случая:
1. К балке приложены 2 равные и противоположные по знаку пары сил. Вводя сечение 1-1 необходимо отметить, что для равновесия каждой части необходим изгибающий момент – результирующий момент внутренних сил, действующих в поперечном сечении нормально к оси. Для левой и правой части относительно сечения внутренний момент имеет противоположное направление.
2. К балке приложены активные и реактивные силы – перпендикулярно оси. Проводя сечение для равновесия балки приходится вводить изгибающие моменты и поперечные силы (что эквивалентно появлению касательных напряжений за счёт поперечных сил; для левой и правой касательные силы противоположного направления), т.е. при таком рассмотрении вводятся Ми и Q. В этом случае изгиб называется поперечным. Проведение сечений в разных местах будет сопровождаться изгибающими моментами и поперечными силами, которые будут иметь неодинаковые значения.
Для балки, находящейся в равновесии, при плоской системе сил алгебраическая сумма моментов всех активных и реактивных сил по отношению к любой точке равна нулю (иначе говоря: сумма моментов внешних сил, действующих левее сечения, равна сумме моментов всех внешних сил, действующих правее сечения).
Для той же балки при равновесии сумма внешних сил левее сечения должна численно равняться сумме сил правее сечения (если силы перпендикулярны оси).
Поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения.
Знаки определяют так: если внешняя сила изгибает балку выпуклостью вниз – Ми > 0 и наоборот; если сумма внешних сил левее сечения имеет равнодействующую, направленную вверх, она > 0 и наоборот. Для сил, лежащих правее сечения, наоборот.
Для определения поперечных сил Q и распределенных нагрузок (по длине) q используют теорему Журавского. Для чего изображают балку и все, приложенные к ней, нагрузки (активные, реактивные, распределённые, моменты); проводят сечение с произвольной координатой z; для него подсчитывают алгебраическую сумму моментов.
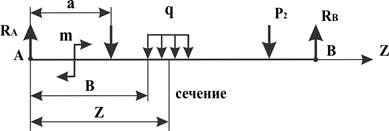
Mu = Ra z + m – P1 (z – a) + q (z-b)2/2
Теорема Журавского: поперечная сила равна первой производной от изгибающего момента по продольной координате; вторая производная от изгибающего момента (или первая от поперечной силы) равна интенсивности распределённой нагрузки.
dMu/dz = Ra – P1 + q(z – b) = Q – поперечная сила и d2Mu/dz2 = dQ/dz = q.
По результатам расчётов строят эпюры поперечных сил и изгибающих моментов, по которым легко определить опасное сечение балки и значения в нём поперечной силы и изгибающего момента.
Эпюры строят двумя способами:
1. Составляют формулы поперечных сил и изгибающих моментов для каждого участка Q = f1(z) и Ми = f2(z) и по формулам строят кривые.
2. Эпюры строят по характерным точкам и значениям Q и Ми по границам участка.
Правила: положительные силы и моменты откладывают вверх; в месте приложения сосредоточенной силы поперечная сила изменяется скачком на величину модуля силы;
в месте приложения момента (пары сил) Ми также меняется скачком на величину момента пары;
правильность построения проверяют с помощью теоремы Журавского (т.к. dMи/dz = Q = tgα при α = 0 Q = 0, Ми = const (или экстремум) – чистый изгиб. При 0 < α < 900 – имеем Q > 0 и Ми возрастает; при 900 < α < 1800 Q < 0 и Ми убывает;
где нет распределённой нагрузки эпюра Ми – наклонная прямая, эпюра Q – прямая параллельная оси (ось всегда должна идти слева - направо);
при наличии распределённой нагрузки эпюра Ми – парабола, а эпюра Q – наклонная прямая;
на конце балки Ми = 0, если нет приложения внешней пары;
если балка консольная – начало координат удобно брать на конце консоли, а в месте заделки Q = R и Ми равен реактивному моменту.
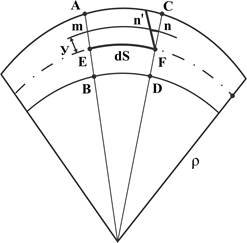 При чистом изгибе существуют только нормальные напряжения растяжения и сжатия.
При чистом изгибе существуют только нормальные напряжения растяжения и сжатия.
Рассмотрим их распределение по поперечному сечению, для чего выделим участок dS между сечениями АВ и СД (радиус кривизны для нейтрального сечения ρ). Волокно mn на nn` удлинится; из-за малости выделенные участки примем за треугольники (они подобны - их соответственные стороны параллельны), т.е. nn`/dS = y/ρ, но nn/dS = ε, следовательно σ = Еε = Еу/ρ, т.е. нормальные напряжения σ = F(y) - распределены по высоте.
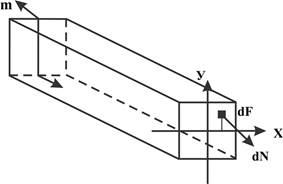 Выделим в сечении участок площадью dF, на которой σ = const и запишем условия равновесия:
Выделим в сечении участок площадью dF, на которой σ = const и запишем условия равновесия:
∑ Z = ∫ dN = 0; ∑ Mx = -m + ∫ ydN = 0;
подробно ∫ σ dF = ∫ EydF/ρ = (E/ρ)∫ ydF = 0, т.к. Е ≠ 0 и ρ ≠ 0, то ∫ ydF = 0, а это статический момент сечения (его равенство нулю означает – ось нейтральная проходит через центр тяжести поперечного сечения).
m+∫ ydN = 0 даёт m = Mи = ∫ ydN = ∫ yσ dF= ∫ (E/ρ)y2dF = (E/ρ)∫ y2dF, интеграл – момент Iρ – момент инерции, т.е. Ми = ЕI/ρ, откуда ρ = ЕI/Mи = const (ось изогнутой балки – дуга окружности).
В итоге: ρ = ЕУ/Ми ; σ = ЕУ/ρ = Ми У/I; σ max = Mи Умах /I = Mи /W, где W = I/Ymax - осевой момент сопротивления изгибу.
При расчётах на прочность при изгибе максимальное нормальное напряжение в опасном сечении на должно превышать допускаемое
σ мах = Ми мах /W ≤ [σ ].
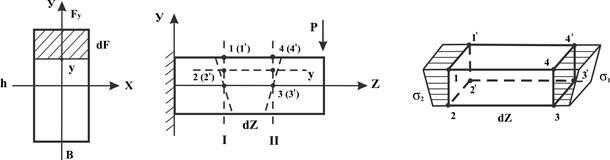 В общем случае в поперечных сечениях возникают и поперечные силы, и изгибающие моменты. Изгибающие моменты рождают продольные напряжения, а поперечные силы создают касательные напряжения (по закону парности касательных напряжений они возникают в поперечных и продольных сечениях). Рассмотрим балку с поперечным сечением bh, выделим малый параллелепипед bdz(h/2 – y)
В общем случае в поперечных сечениях возникают и поперечные силы, и изгибающие моменты. Изгибающие моменты рождают продольные напряжения, а поперечные силы создают касательные напряжения (по закону парности касательных напряжений они возникают в поперечных и продольных сечениях). Рассмотрим балку с поперечным сечением bh, выделим малый параллелепипед bdz(h/2 – y)
В сечении 1 действует изгибающий момент Ми и нормальная сила N1, в сечении 11 Ми + dMи и N2
N1 = ∫ σ z dF = (Mи /I)∫ ydF; N2 = ∫ σ 1dF = ((Mи + dMи )/I)∫ ydF.
В поперечных сечениях τ ║ Q и распределены равномерно по сечению и в силу парности касательных напряжений в продольном сечении возникает сила касательная продольному сечению dT = τ bdz.
Для выделенного объёма 11'2'2, который внутри материала находится в равновесии, записываем условия равновесия:
∑ Z = 0 = N1 +dT – N2 , что даёт dT = N2 – N1 = (dMи/I)∫ ydF = (dMи/I)S или τ bdZ = (dMи/I)S; т.е.
τ = (dMи /dZ) (S/Ib = QS/Ib)
касательное напряжение в поперечном сечении балки равно частному отделению произведения поперечной силы и статического момента отнросительно нейтральной оси части сечения, лежащего выше рассматриваемого слоя волокон, на произведение момента инерции всего сечения относительно нейтральной оси и ширины рассматриваемого слоя волокон.
Для прямоугольного сечения, подставляя S и I, получим
τ = QS/Ib = 6Q/bh3(h2/4 – y2)
касательное напряжение неравномерно распределено по высоте в сечении балки (у поверхности равно нулю, а на оси достигает максимума).