Метод вспомогательных секущих эксцентрических сфер

На рис. 29 представлены фронтальные проекции пересекающихся поверхностей вращения: усеченного конуса и тора (кольца). Поверхности имеют общую главную меридианальную плоскость, являющуюся одновременно и плоскостью симметрии фигур. Поэтому фронтальные проекции поверхностей вращения представляют собой их главные меридианы. Оси вращения поверхностей являются скрещивающимися прямыми, причем ось вращения усеченного конуса i^к является профильно-проецирующей прямой, а ось вращения тора i^т — фронтально-проецирующей прямой. Задача ограничена построением только фронтальной проекции линии взаимного пересечения поверхностей.

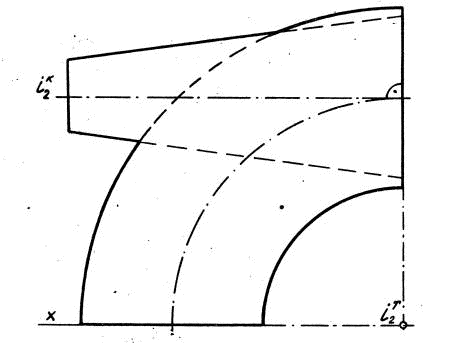
Рис. 29.

Использовать способ вспомогательных секущих плоскостей и способ концентрических сфер для определения положения на чертеже проекций точек кривой взаимного пересечения поверхностей невозможно. Так при пересечении заданных на чертеже поверхностей вращения, например, общей плоскостью в сечении получаются графически сложные кривые линии при любом ее положении. Способ же концентрических секущих сфер здесь не применим, так как оси вращения фигур не пересекаются. Поэтому используем способ эксцентрических секущих сфер. Этот способ предопределяет необходимость выявления наличия для каждой из поверхностей вращения соосной секущей сферы (рис. 30).

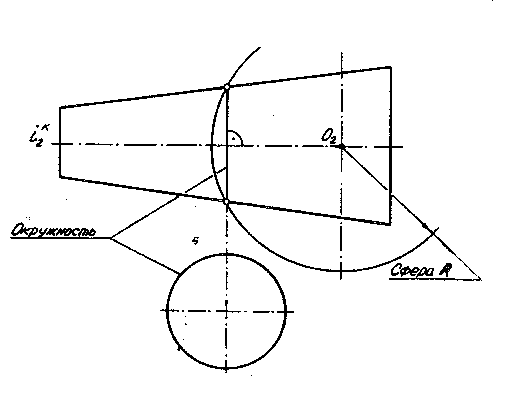
Рис. 30.

Для поверхности усеченного конуса определение положения соосной сферы следует из определения соосности двух поверхностей вращения — сфера соосна с конической поверхностью в том случае, когда центр сферы располагается непосредственно на оси вращения конуса. Только в этом случае в пересечении указанных поверхностей образуется окружность. Положение сферы соосной с поверхностью тора (рис. 31) устанавливают следующим образом.

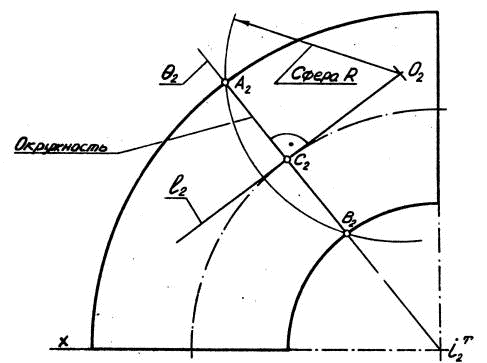
Рис. 31.

Известно, что в случае пересечения поверхности вращения плоскостью, проходящей через ее ось, в сечении образуется меридиан. Меридианом же тора является окружность. Поэтому при пересечении поверхности тора фронтально-проецирующей плоскостью θ, проходящей через его ось i^т, в сечении образуется окружность.

Фронтальная проекция окружности сечения тора плоскостью θ представляет собой отрезок A ₂ B ₂. Фронтальная проекция центра окружности сечения располагается в точке C ₂ и представляет собой точку пересечения следа θ ₂ секущей плоскости θ с проекцией траектории движения (вращения) центра меридиана поверхности. Тогда фронтальная проекция O ₂центра соосной сферы, пересекающейся с заданной поверхностью тора по окружности, должна располагаться на прямой l ₂, проходящей через точку C ₂ в направлении перпендикулярном отрезку A ₂ B ₂ (рис. 31).

Выявив наличие соосных сфер для каждой из поверхностей вращения — усеченного конуса и тора, устанавливают возможность проведения общей для них соосной секущей сферы. Для этого вначале определяют положение опорных точек 1₂ и 2₂ пересечения главных меридианов поверхностей, ограничивающих положение на чертеже фронтальных проекций регулярных точек кривой взаимного пересечения заданных поверхностей (рис. 32).

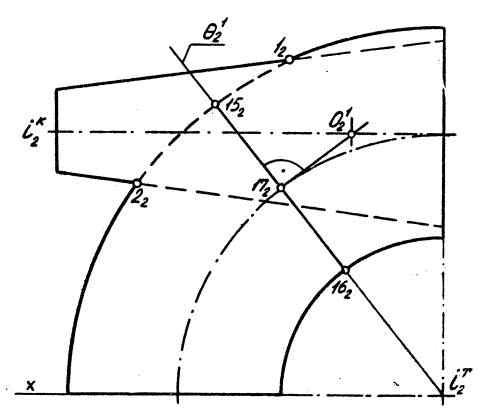
Рис. 32.

Затем между проекциями опорных точек 1₂ и 2₂ проводят след θ ₂¹ первой секущей фронтально-проецирующей плоскости, проходящей через проекцию оси вращения тора i ₂ ^т.

Проведение вспомогательной секущей плоскости θ ¹ позволяет выявить на чертеже положение центра сферы, соосной с поверхностью тора. Если прямую, на которой должна располагаться фронтальная проекция центра соосной сферы, продолжить до пересечения с проекцией i ₂ ^k — оси вращения усеченного конуса, то получится точка O ₂¹, представляющая собой теперь уже центр сферы, соосной с каждой из заданных поверхностей вращения. Подобным приемом графического построения можно определить положения на чертеже некоторого количества центров секущих сфер, соосных с каждой из поверхностей. Далее на чертеже (рис. 33) из центра O ₂¹ радиусом, равным отрезку O ₂¹ — 15₂¹, проводят первую секущую соосную сферу. Отмечают точки 18₂ и 19₂ пересечения сферы с главным меридианом усеченного конуса и соединяют их отрезком 18₂ — 19₂.

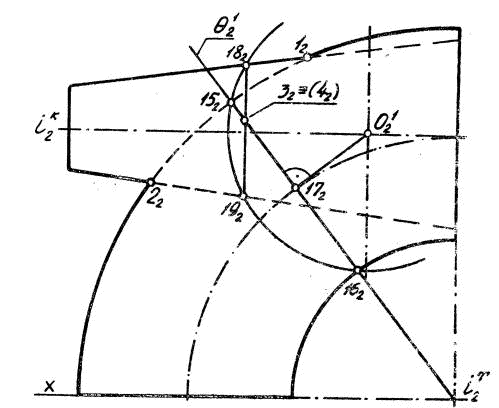
Рис. 33.

Отрезки 15₂ — 16₂ и 18₂ — 19₂ представляют собой фронтальные проекции окружностей сечения каждой из заданных поверхностей вращения одной и той же соосной секущей сферой θ ¹. В пересечении отрезков 15₂ — 16₂ и 18₂ — 19₂ найдены положения проекций 3₂ и 4₂ двух конкурирующих точек. Точки 3 и 4 принадлежат каждой из поверхностей вращения и являются регулярными точками кривой пересечения тора и усеченного конуса. Аналогично (рис. 34) на чертеже определяют положение фронтальных проекций некоторого количества регулярынх точек кривой пересечения.

Соосные сферы проводятся каждый раз из нового центра, поэтому данный способ построений называется способом эксцентрических секущих сфер.

Построение горизонтальных проекций точек кривой пересечения поверхностей основано на эпюрном признаке принадлежности точки

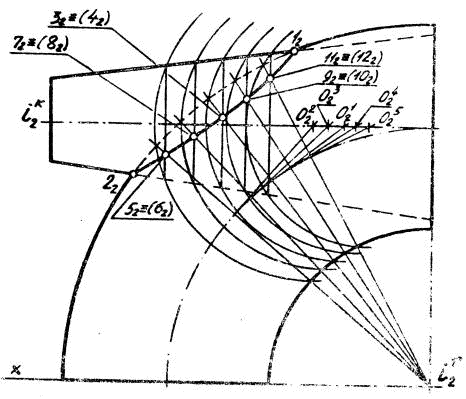
Рис. 34.

поверхности и не вызывает особых затруднений. При этом надо иметь ввиду, что не все точки кривой будут видимыми на горизонтальной плоскости проекций. Поэтому сначала надо определить положение проекций точек видимости.

Соединив плавной кривой одноименные проекции точек, получают горизонтальную и фронтальную проекции кривой пересечения усеченного конуса и тора.

В заключение отметим, что на последовательность графических построений центров соосных секущих сфер влияют вид и расположение на чертеже пересекающихся поверхностей вращения.