Расчетные формулы

Точечные оценки коэффициентов корреляции

Проводится n наблюдений.

Результаты наблюдений – исходная матрица данных:

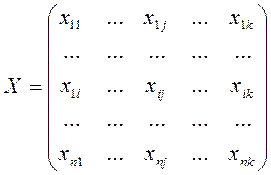
Столбцы характеризуют признаки, строки характеризуют наблюдения (объекты)

Матрицу X рассматриваем как выборку объема 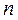, из 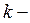мерной генеральной совокупности.

По выборке определяют точечные оценки параметров генеральной совокупности, а именно:

Числовые характеристики	Их оценки
вектор математических ожиданий	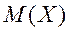вектор выборочных средних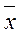
вектор среднеквадратических отклонений	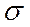Вектор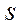
корреляционная матрица	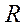выборочная корреляционная матрица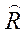

где

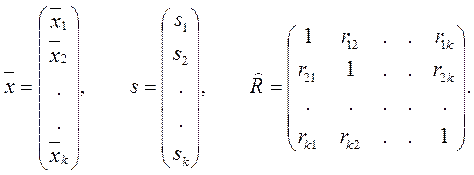
и

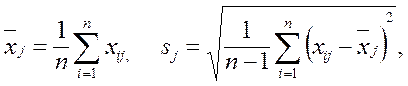(1)

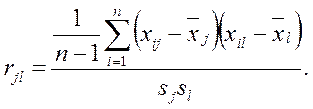(2)

Расчетные формулы

1 способ

а. Сначала рассчитывается выборочные дисперсии, которые являются смещенными оценками дисперсий:

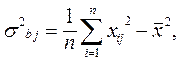
б. Рассчитываются несмещенные дисперсии:

;

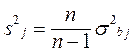в. ,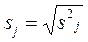

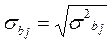
г. .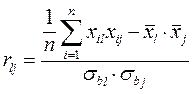

Если объем выборки большой (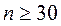), то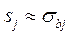

2 способ

а. Сразу рассчитываются несмещенные дисперсии:

;

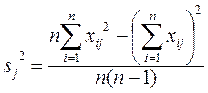б. ;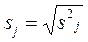

в. .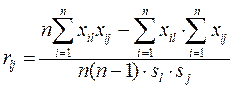

Частный коэффициент корреляции между факторам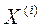и и 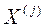равен:

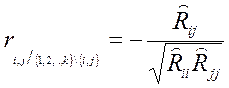(3)

где 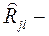алгебраическое дополнение элемента выборочной корреляционной матрицы.

Если 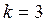, то

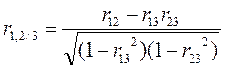(4)

Аналогично,

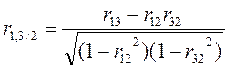и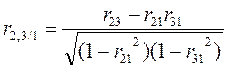

Множественный коэффициент корреляции, например, признака 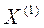определяется по формуле:

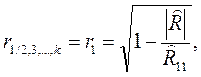(5)

где 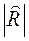- определитель матрицы . В случае трех признаков ():

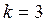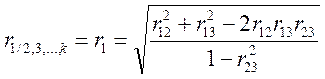. (6)

Следует иметь в виду, что большая величина коэффициента корреляции не является доказательством того, что между исследуемыми признаками существует причинно-следственная связь, а представляет собой оценку степени взаимной согласованности в изменениях признаков.

Для того чтобы установить причинно-следственную зависимость, необходим анализ качественной природы явлений.