Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЧАСТЬ 1. Федеральное агентство по образованию
|
|
Федеральное агентство по образованию
Пермский институт (филиал) ГОУ ВПО
«Российский государственный торгово-экономический университет»
Кафедра Высшей и прикладной
математики
УТВЕРЖДЕНО:
Методическим Советом
ПИ (ф) ГОУ ВПО «РГТЭУ»
Протокол №________
от «___» _________ 200 г.
ПРИКЛАДНАЯ МАТЕМАТИКА
ЧАСТЬ 1
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ №1 ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ ВСЕХ СПЕЦИАЛЬНОСТЕЙ И НАПРАВЛЕНИЙ
Пермь 2006
Методические указания составлены в соответствии с государственными образовательными стандартами второго поколения и программой РГТЭУ.
Р А С С М О Т Р Е Н О:
на заседании кафедры:
Высшей и прикладной математики
от «» 200 г. Протокол №
Зав. каф., к.т.н., профессор В.В. Козлов
Составители: доцент Козлов В.В. доцент Овчинникова В.И.
I. Общие методические указания
Преподавание дисциплины " Прикладная математика" обосновывается на необходимости изучения арсенала математических методов и моделей для применения их в решении практических задач в различных сферах коммерческой и финансовой деятельности, позволяющие получить более выгодные, оптимальные решения в сравнении с традиционными приемами, привить навыки самостоятельного изучения литературы по математическим методам решения коммерческих задач, развить логическое мышление, повысить уровень математической культуры, выработать навыки математического исследования проблем и задач финансовой и коммерческой деятельности.
Курс изучается по программе " Прикладная математика", утвержденной в 1992 г.
Цель настоящих методических указаний (часть I) - оказать помощь студентам в изучении разделов и тем курса " Прикладная математика" для развития навыков по применению различных математических методов и моделей в решении практических задач коммерческой деятельности, а также подготовить к самостоятельному изучению литературы по математическим методам в экономике и применения их к решению новых проблем и задач в финансовой и коммерческой сферах.
II. Литература
1. Кузнецов Ю.П. Математическое программирование. - М.: Высшая школа, 1980.
2. Вентцель Е.С. Исследование операций. М.: Наука, 1980.
3. Спирин А.А., Фомин Г.П. Экономико-математические методы и модели в торговле М.: Экономика, 1988.
4. Дж. Хедли Нелинейное и динамическое программирование, М.: Мир, 1967.
5. Фомин Г.П., Шарипов ГА. Экономико-математическое моделирование явлений и процессов в торговле: Учеб. пособие /Заоч. ин-т сов. торговли, М., 1982
6. Фомин Г.П., Григорьев С.Б. Модели оптимального планирования в общественном питании: Учеб. Пособие/ Моск. коммерческий ин-тМ., 1990.
7.. Фомин Г.П., Системы и модели массового обслуживания в общественном питании: Учеб. пособие/Заочн. ин-т сов. Торговли М., 1987.
8. Фомин Г.П., Модели выбора решений в коммерческих операциях М.: изд-во МГУК, 1996, 29с.
9. Смирнова В.В. Методические указания и задания по дисциплине «Математическое программирование», М., МУПК, 1998..
10. Смирнова В.В. Методические указания и задания по дисциплине " Математическое программирование", М:, МУПК.1998.
Для выполнения контрольной работы студенту необходимо ознакомится с программой курса " Прикладная математика", с методическими указаниями и контрольными заданиями. При изучении студент должен пользоваться рекомендуемой литературой, материалами устных и письменных консультаций, закрепляя усвоение каждой темы решением практических задач.
Студент, завершивший самостоятельное изучение дисциплины, должен выполнить две контрольные работы и сдать экзамен.
III. ЗАДАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ №1
Предлагаются к самостоятельному изучению и последующему решению задач по следующим темам:
1. Решение задачи линейного программирования на основе ее геометрической интерпретации (графический метод).
2. Моделирование экономических процессов коммерческого предприятия и решение моделей симплексным методом.
3. Двойственная задача к задаче планирования работы коммерческого предприятия.
4. Транспортная задача в матричной постановке. Построение первого опорного плана. Нахождение оптимального плана транспортной задачи методом потенциалов.
5. Номера задач определяются в соответствии с таблицей 1 по первым буквам фамилии, имени, отчества.
Таблица 1
| Первые буквы | Номера задач для контрольного задания | ||
| Фамилия | Имя | Отчество | |
| А | 51 76 | ||
| Б | 52 77 | ||
| В | 53 78 | ||
| Г | 54 79 | ||
| Д | 55 80 | ||
| Е | 56 81 | ||
| Ж | 57 82 | ||
| 58 83 | |||
| И | 59 84 | ||
| к | 60 85 | ||
| л | 61 86 | ||
| м | 62 87 | ||
| н | 63 88 | ||
| 64 89 | |||
| п | 65 90 | ||
| р | 66 91 | ||
| с | 67 92 | ||
| т | 68 93 | ||
| У | 69 94 | ||
| ф | 70 95 | ||
| Х | 71 96 | ||
| Ц | 72 97 | ||
| ч | 73 98 | ||
| шэ | 74 99 | ||
| юя | 75 100 |
ЗАДАЧИ № 1 - 25
Построить на плоскости область решений системы линейных неравенств и найти максимальное и минимальное значения линейной функции в этой области.
1. 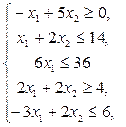 5.
5. 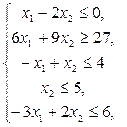




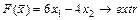
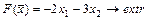
2. 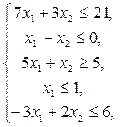 6.
6. 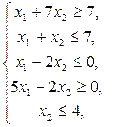




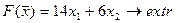
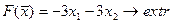
3. 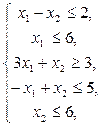 7.
7. 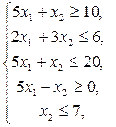




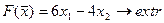
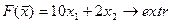
4.  8.
8. 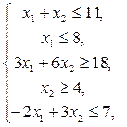




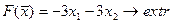
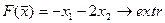
9. 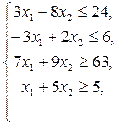 10.
10. 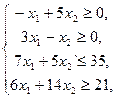




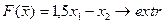
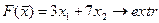
11. 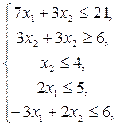 12.
12. 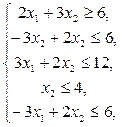




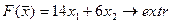
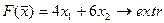
13. 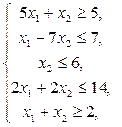 14.
14. 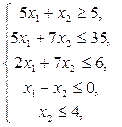




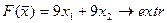
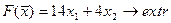
16. 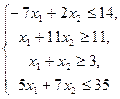 17.
17. 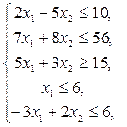




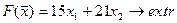

18. 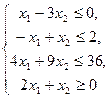 19.
19. 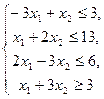




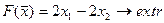
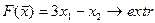
20. 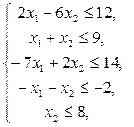 21.
21. 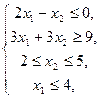




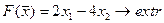
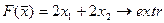
22. 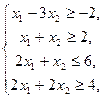 23.
23. 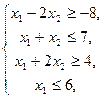




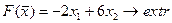
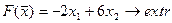
24. 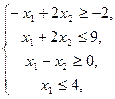 25.
25. 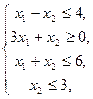




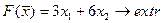
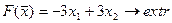
Задачи № 26 - 50
Для реализации трех групп товаров коммерческое предприятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве  единиц. При этом для продажи 1 группы товаров на 1 тыс. руб. товарооборота расходуется ресурса первого вида в количестве
единиц. При этом для продажи 1 группы товаров на 1 тыс. руб. товарооборота расходуется ресурса первого вида в количестве 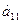 единиц, ресурса второго вида в количестве
единиц, ресурса второго вида в количестве 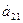 единиц, ресурса третьего вида в количестве
единиц, ресурса третьего вида в количестве 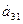 единиц. Для продажи 2 и 3 групп товаров на 1 тыс. руб. товарооборота расходуется соответственно ресурса первого вида в количестве
единиц. Для продажи 2 и 3 групп товаров на 1 тыс. руб. товарооборота расходуется соответственно ресурса первого вида в количестве 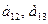 единиц, ресурсов второго вида в количестве
единиц, ресурсов второго вида в количестве 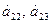 единиц, ресурсов третьего вида в количестве
единиц, ресурсов третьего вида в количестве 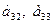 единиц. Прибыль от продажи трех групп товаров на 1 тыс. руб. товарооборота составляет соответственно
единиц. Прибыль от продажи трех групп товаров на 1 тыс. руб. товарооборота составляет соответственно 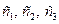 (тыс. руб.).
(тыс. руб.).
Определить плановый объем и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.
26. а11=3, а12=6, а13=4, a21=2, а22=1, а23=2, а31=2, а32=3, а33=1, b1=180, Ь2=50, Ь3=40, C1=6, С2=5, С3=5.
27. а11=1, а12=2, а13=1, а21=2, а22=1, а23=3, а31=4, а32=2, а33=1, b1=420, Ь2=600, Ь3=900, c1=3, С2=3, С3=4.
28. a11=16, а12=18, а13=9, a21=7, a22=7, a23=2, a31=9, a32=2, a33=3, Ь1=520, Ь2=140, Ь3=810, c1=8, с2=6, С3=4.
29. а11=4, а12=8, а13=2, а21=3, а22=8, а23=4, а31=12, а32=4, а33=6, b1=116, Ь2=240, Ь3=432, C1=8, с2=6, С3=6.
30. а11=8, a12=10, a13=20, a21=4, a22=13, a23=8, a31=2, a32=18, a33=12, b1=800, Ь2=520, Ь3=940, c1=3, c2=6, С3=7.
31. а11=3, а12=3, а13=9, a21=10, a22=9, a23=15, a31=5, a32=5, a33=1, b1=810, Ь2=900, Ь3=250, C1=7, c2=7, C3=6.
32. а11=17, а12=5, а13=5, а21=8, а22=6, а23=6, а31=4, а32=2, а33=4, b1=850, Ь2=1120, Ь3=1060, d=8, С2=7, с3=4.
33. а11=2, a12=1, a13=6, а21=3, а22=3, а23=9, a31=2, a32=1, азэ=2, Ь1=240, Ь2=540, Ь3=120, c1=14, С2=6, С3=22.
34. а11=2, а12=3, а13=6, а21=6, а22=8, а23=2, a31=3, a32=43, а33=2, Ь1=450, Ь2=400, Ь3=350, с1=З, С2=5, С3=4.
35. a11=1, a12=1, a13=1, a21=2, а22=1, а23=3, а31=3, аз2=2, азз=3, b1=160, Ь2=200, Ь3=240, c1=4, С2=3, С3=5.
36. а11=2, a12=3, а13=6, а21=4, а22=2, а23=4, а31=4, а32=6, а33=8, b1=240, Ь2=200, Ь3=160, C1=4, С2=5, С3=4.
37. а11=9, а12=9, a13=2, a21=4, a22=3, a23=2, a31=1, a32=2, a33=4, b1=180, Ь2=120, Ь3=220, c1=7, c2=8, C3=6.
38. а11=18, а12=9, а13=6, а21=4, а22=2, а23=4, a31=3, a32=3, а33=1, b1=540, Ь2=340, Ь3=120, с1=3, С2=4, с3=3.
39. а11=3, а12=2, a13=1, a21=4, а22=2, а23=4, а31=3, а32=3, а33=4, b1=70, bz=80, Ь3=120, c1=7, с2=8, с3=7.
40. а11=4, а12=2, a13=5, a21=2, а22=8, а23=4, a31=11, a32=4, a33=2, Ь1=250, Ь2=160, Ь3=440, c1=7, С2=6, С3=8.
41. а11=7, a12=4, a13=5, a21=6, a22=2, a23=4, a31=7, a32=14, а33=7, Ь1=280, Ь2=160, Ь3=420, С1=18, С2=16, С3=15.
42. а11=5, а12=8, а13=4, а21=5, а22=5, а23=6, a31=10, a32=2, азз=5, b1=400, Ь2=300, Ь3=200, c1=4, C2=3, С3=2.
43. a11=5, а12=5, a13=2, а21=4, а22=6, а23=8, a31=5, а32=6, а33=2, b1=250, Ь2=500, Ь3=300, c1=10, с2=, с3=9.
44. а11=7, a12=7, а13=4, a21=2, a22=4, a23=8, a31=16, аЭ2=12, а33=10, Ь1=280, Ь2=160, Ь3=530, с1=10, с2=10, c3=12.
45. а11=7, а12=10, а13=11, а21=8, а22=б, а23=4, a31=12, a32=4, а33=16, b1=740, Ь2=820, Ь3=480, c1=10, с2=8, с3=7.
46. а11=2, а12=2, а13=4, а21=1, а22=5, а23=1, a31=6, a32=2, а33=1, Ь1=540, Ь2=360, Ь3=180, c1=3, с2=2, с3=1.
47. а11=10, а12=6, а13=8, a21=6, а22=6, а23=4, а31=10, а32=12, а33=6, Ь1=840, Ь2=296, Ь3=620, c1=6, с2=5, с3=5.
48. a11=10, а12=5, а13=10, а21=26, а22=13, а23=4, а31=3, а32=4, а33=2, Ь1=670, Ь2=520, Ь3=480, c1=8, с2=6, с3=6.
49. а11=9, а12=9, а13=3, а21=3, а22=6, а23=9, a31=7, a32=4, а33=12, Ь1=801, Ь2=453, Ь3=280, c1=3, с2=2, с3=2.
50. а11=10, а12=5, а13-5, а21=7, а22=2, а23=4, а31=7, а32=3, а33=3, Ь, =290, Ь2=140, Ь3=210, c1=10, с2=9, с3=5.
Задачи №51-75
Используя вариант предыдущего контрольного задания №25-50, необходимо:
- к прямой задаче планирования товарооборота, решаемой симплексным методом, составить двойственную задачу линейного программирования;
- установить сопряженные пары переменных прямой и двойственной задач;
- согласно сопряженным парам переменных из решения прямой задачи получить решение двойственной задачи, в которой производится оценка ресурсов, затраченных на продажу товаров.
Задачи №76-100
Поставщики товара - оптовые коммерческие предприятия 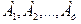 имеют запасы товаров соответственно в количестве
имеют запасы товаров соответственно в количестве 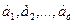 ед. и розничные торговые предприятия
ед. и розничные торговые предприятия 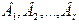 - подали заявки на закупку товаров в объемах соответственно:
- подали заявки на закупку товаров в объемах соответственно: 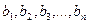 . Тарифы перевозок единицы груза с каждого из пунктов поставки в соответствующие пункты потребления заданы в виде матрицы
. Тарифы перевозок единицы груза с каждого из пунктов поставки в соответствующие пункты потребления заданы в виде матрицы
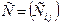 (
( =
= 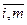 ; j = i, n)
; j = i, n)
Найти такой план перевозки груза от поставщиков к потребителям, чтобы совокупные затраты на перевозку были минимальными.
76. 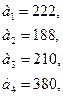
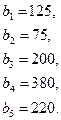
C = 
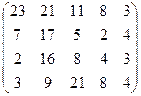
77. 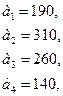
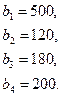
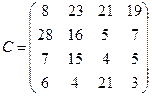
78. 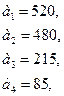

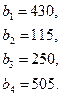
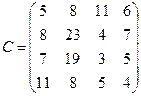
79. 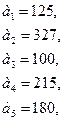
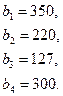
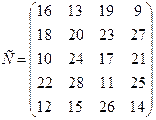
80. 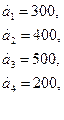
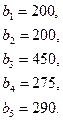
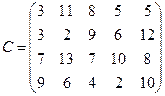
81. 
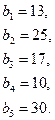
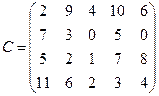
82. 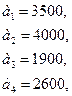
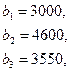
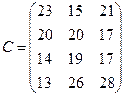
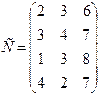 83.
83. 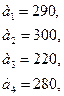
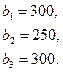
84. 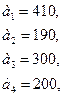
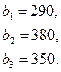
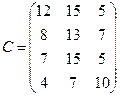
85. 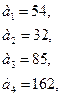
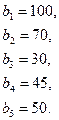
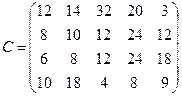
86. 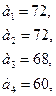
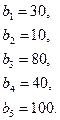
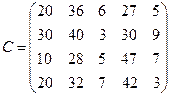
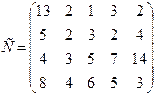 87.
87. 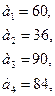
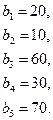
88. 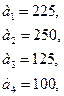
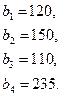
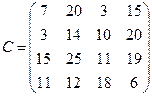
89. 
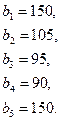
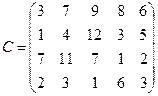
90. 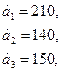
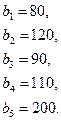
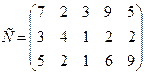
91. 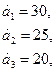
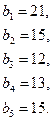
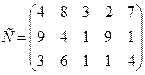
92. 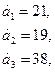
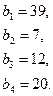
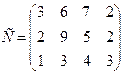
93. 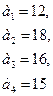
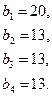
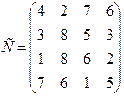
94. 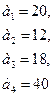
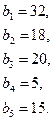
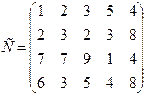
95. 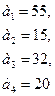
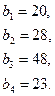
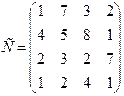
96. 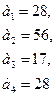
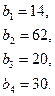
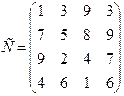
97. 
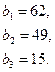
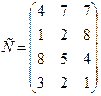
98. 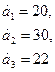

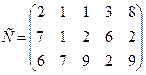
99. 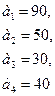
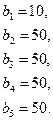
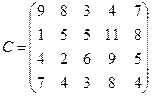
100. 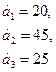

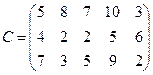
ПРАВИЛА ОФОРМЛЕНИЯ РАБОТЫ
На титульном листе тетради должны быть написаны наименование дисциплины, наименование факультета, курс, фамилия, имя, отчество.
В начале работы или на титульном листе должны быть указаны номера задач, выполненных в контрольном задании.
Перед решением каждой задачи надо полностью записать ее условие. Решение задач должно включать развернутые расчеты и краткие пояснения, экономический анализ полученных результатов. В конце контрольной работы привести список использованной литературы и поставить свою подпись.
В процессе выполнения контрольной работы студент может получить на кафедре устную или письменную консультацию.
Допущенную к защите контрольную работу вместе с рецензией на нее студент должен представить на собеседование.
Студент, не выполнивший контрольную работу и не прошедший собеседование, к экзамену не допускается.
IV.МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
1. Графический метод решения задач линейного программирования
Общей задачей линейного программирования ОЗЛП называется задача, которая состоит в определении максимального (минимального) значения линейной целевой функции:
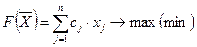
При условиях-ограничениях
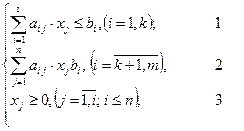
где 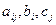 -заданные постоянные величины и
-заданные постоянные величины и 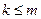 .
.
Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения целевой функции при выполнении условий 1 и 3, где  и
и 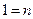 .
.
Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения целевой функции при выполнении условий 2 и 4, где 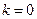 и
и 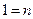 .
.
Совокупность чисел 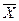 =
= 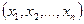 удовлетворяющих ограничениям задачи, называется допустимым решением (или планом).
удовлетворяющих ограничениям задачи, называется допустимым решением (или планом).
План 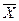 =
= 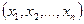 , при котором целевая функция задачи принимает максимальное (минимальное) значение, называется оптимальным.
, при котором целевая функция задачи принимает максимальное (минимальное) значение, называется оптимальным.
В случае, когда требуется найти минимум функции 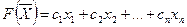 можно перейти к нахождению максимума функции
можно перейти к нахождению максимума функции 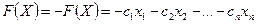 , так как min
, так как min 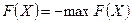 .
.
Ограничение-неравенство исходной задачи линейного программирования, имеющее вид " 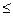 ", преобразуется в ограничение-равенство добавлением к левой части дополнительных неотрицательной переменной, а ограничение неравенство вида "
", преобразуется в ограничение-равенство добавлением к левой части дополнительных неотрицательной переменной, а ограничение неравенство вида " 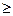 " - в ограничение-равенство вычитанием из левой части дополнительной неотрицательной переменной.
" - в ограничение-равенство вычитанием из левой части дополнительной неотрицательной переменной.
Допустим ограничения задачи отображают наличие производственных ресурсов, тогда числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.
План 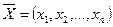 называется опорным планом основной задачи линейного программирования, если система векторов, входящих в разложение с положительными коэффициентами
называется опорным планом основной задачи линейного программирования, если система векторов, входящих в разложение с положительными коэффициентами 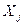 линейно независима.
линейно независима.
Так как векторы 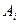 являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может превышать m.
являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может превышать m.
Опорный план называется невырожденным, если он содержит ровно m положительных компонент, в противном случае - план вырожденный.
Свойства основной задачи линейного программирования связаны со свойствами выпуклых множеств.
Множество точек называется выпуклым, если оно вместе с любыми двумя точками содержит и их произвольную выпуклую линейную комбинацию.
Геометрический смысл этого определения состоит в том, что множеству вместе с его двумя произвольными точками полностью принадлежит и прямолинейный отрезок, их соединяющий. Примерами выпуклых множеств являются прямолинейный отрезок, полуплоскость, круг, шар, куб, полупространство и др.
Угловыми точками выпуклого множества называются точки, не являющиеся выпуклой комбинацией двух произвольных точек множества. Например, угловыми точками треугольника являются его вершины, круга - точки окружности, которые его ограничивают.
Множество планов основной задачи линейного программирования является выпуклым (если оно не пусто). Непустое множество планов называется многогранником решений, а всякая угловая точка многогранника решений - вершиной.
Если основная задача линейного программирования имеет оптимальный план, то максимальное значение целевая функция задачи принимает в одной из вершин многогранника решений. Если максимальное значение достигается более чем в одной вершине, то целевая функция принимает его во всякой точке, являющейся выпуклой линейной комбинацией этих вершин.
Непустое множество планов основной задачи линейного программирования образует выпуклый многогранник, каждая вершина которого определяет опорный план. Для одного из опорных планов (т.е. в одной из вершин многогранника решений) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов).
Вершину многогранника решений, в которой целевая функция принимает максимальное значение, можно найти достаточно просто, если задача в стандартной форме содержит не более двух переменных:

при условиях
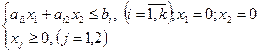
Каждое из неравенств системы ограничений задачи геометрически определяет полуплоскость допустимых значений переменных соответственно с граничными прямыми

Если система неравенств совместна, то областью допустимых решений задачи является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.
Решение задачи линейного программирования графическим методом включает следующие этапы.
1. На плоскости 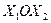 строят прямые, уравнения которые получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.
строят прямые, уравнения которые получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.
2. Находят полуплоскости, определяемые каждым из ограничений задачи.
3. Строят многоугольник решений.
4. Строят вектор 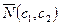 , направление которого указывает на возрастание целевой функции.
, направление которого указывает на возрастание целевой функции.
5. Строят начальную прямую 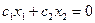 и передвигают ее в направлении вектора
и передвигают ее в направлении вектора 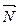 до крайней угловой точки многоугольника решений. В результате находят точку, в которой целевая функция принимает максимальное значение, либо множество точек с одинаковым максимальным значением целевой функции, если начальная прямая сливается с одной из сторон многоугольника решений, либо устанавливают неограниченность сверху функции на множестве планов
до крайней угловой точки многоугольника решений. В результате находят точку, в которой целевая функция принимает максимальное значение, либо множество точек с одинаковым максимальным значением целевой функции, если начальная прямая сливается с одной из сторон многоугольника решений, либо устанавливают неограниченность сверху функции на множестве планов 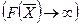 .
.
6. Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.
Минимальное значение линейной функции цели находится путем передвижения начальной прямой 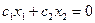 , в направлении,
, в направлении,
противоположном вектору 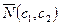 .
.
Пример
Найти максимум и минимум линейной функции:
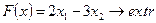 при условиях:
при условиях:

Решение;
Построим на плоскости 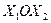 многоугольник решений рис.1.
многоугольник решений рис.1.
Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств.
|
Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение
Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение
Многоугольником решений задачи является пятиугольник АВ-СДЕ, координаты точек которого удовлетворяют условию неотрицательности и неравенствам системы ограничений задачи.
Для нахождения точек экстремума построим начальную прямую 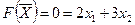 и вектор
и вектор 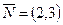 . Передвигая прямую
. Передвигая прямую 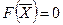 параллельно самой себе в направлении вектора
параллельно самой себе в направлении вектора 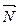 , найдем точку С, в которой начальная прямая принимает положение опорной прямой. Следовательно, в точке С целевая функция принимает максимальное значение, так как точка С получена в результате пересечения прямых 1 и 2, то ее координаты удовлетворяют уравнениям этих прямых:
, найдем точку С, в которой начальная прямая принимает положение опорной прямой. Следовательно, в точке С целевая функция принимает максимальное значение, так как точка С получена в результате пересечения прямых 1 и 2, то ее координаты удовлетворяют уравнениям этих прямых:
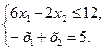
Решив систему уравнений, получим: 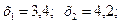
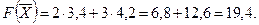
Для нахождения минимального значения целевой функции задачи перемещаем начальную прямую в направлении, противоположном вектору 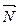 . Начальная прямая займет положение опорной прямой в вершине Е. Целевая функция принимает минимальное
. Начальная прямая займет положение опорной прямой в вершине Е. Целевая функция принимает минимальное
значение в угловой точке Е, где 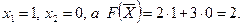
Найдем координаты угловых точек В, Д и А. Для этого решим следующие системы уравнений:

В результате получим координаты точек В (0; 2, 5), Д (2, 0) и А (0, 1).
Вычислим значения целевой функции во всех угловых точках многоугольника решений АВСДЕ:
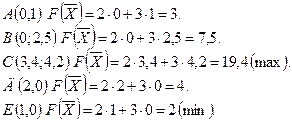
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте общую задачу линейного программирования.
2. Дайте определение невырожденного и вырожденного опорного плана, оптимального плана.
3. Какое множество называется выпуклым?
4. Какая точка выпуклого множества называется угловой?
5. Дайте геометрическую интерпретацию задачи линейного программирования.
6. В какой точке многогранника решений целевая функция задачи линейного программирования достигает оптимального значения?
7. Какие задачи линейного программирования можно решить графическим методом?
8. Назовите особые случаи при решении задачи линейного программирования графическим методом.
2. Симплексный метод решения задачи линейного программирования.
Симплексный метод основан на последовательном переходе от одного опорного плана задачи линейного программирования к другому, при этом значение целевой функции изменяется. Рассмотрим алгоритм симплексного метода на примере задачи планирования товарооборота.
Коммерческое предприятие реализует несколько 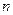 -товарных групп, располагая
-товарных групп, располагая 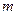 ограниченными материально-денежными ресурсами
ограниченными материально-денежными ресурсами 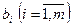 . Известны расходы ресурсов каждого
. Известны расходы ресурсов каждого 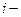 вида на реализацию продажи единицы товарооборота товаров по каждой группе, представленной в виде матрицы
вида на реализацию продажи единицы товарооборота товаров по каждой группе, представленной в виде матрицы 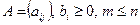 и прибыль
и прибыль 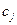 получаемая предприятием от реализации единицы товарооборота товаров
получаемая предприятием от реализации единицы товарооборота товаров 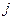 группы. Определить объем и структуру товарооборота
группы. Определить объем и структуру товарооборота 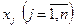 . при которых прибыль коммерческого предприятия была бы максимальной.
. при которых прибыль коммерческого предприятия была бы максимальной.
1. Математическую модель задачи запишем следующим образом:
Определить 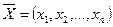 , который удовлетворяет ограничениям вида:
, который удовлетворяет ограничениям вида:
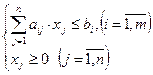
и обеспечивает максимальное значение целевой функции
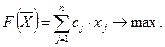
Алгоритм симплексного метода включает следующие этапы.
2. Составление первого опорного плана.
Система ограничений задачи, решаемой симплексным методом, задана в виде системы неравенств. Перейдем от системы неравенств к системе уравнений путем введения неотрицательных дополнительных переменных. Векторы-столбцы при этих переменных представляют собой единичные векторы и образуют базис, а соответствующие им переменные называются базисными:
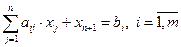
где 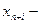 базисные переменные.
базисные переменные.
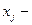 свободные переменные.
свободные переменные.
Решим эту систему относительно базисных переменных:
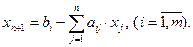
а функцию цели перепишем в таком виде:
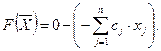
Полагая, что основные переменные 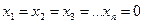
.получим первый опорный план 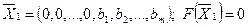 , (заносим его в симплексную таблицу 3, которая состоит из коэффициентов системы ограничений и свободных членов. Последняя строка таблицы называется индексной. Она заполняется коэффициентами функции цели, взятыми с противоположным знаком.
, (заносим его в симплексную таблицу 3, которая состоит из коэффициентов системы ограничений и свободных членов. Последняя строка таблицы называется индексной. Она заполняется коэффициентами функции цели, взятыми с противоположным знаком.
3. Проверка плана на оптимальность.
Если все коэффициенты индексной строки симплексной таблицы при решении задачи на максимум неотрицательны (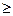 0), то
0), то
план табл.3 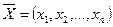 задачи табл. 2 является оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный и его можно улучшить. Тогда переходим к следующему этапу алгоритма.
задачи табл. 2 является оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный и его можно улучшить. Тогда переходим к следующему этапу алгоритма.
4. Определение ведущих столбца и строки.
Из отрицательных коэффициентов индексной строки выбираем наибольший по абсолютной величине, что и определяет ведущий столбец, который показывает, какая переменная на следующей итерации перейдет из свободных в базисные.
Затем элементы столбца свободных членов симплексной таблицы делим на соответствующие только положительные элементы ведущего столбца. Результаты заносим в отдельный столбец 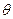 . Строка симплексной таблицы, соответствующая минимальному значению
. Строка симплексной таблицы, соответствующая минимальному значению 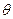 , является ведущей. Она определяет переменную
, является ведущей. Она определяет переменную 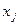 которая на следующей итерации выйдет из базиса и станет свободной.
которая на следующей итерации выйдет из базиса и станет свободной.
Элемент симплексной таблицы, находящейся на пересечении ведущих столбца и строки, называют разрешающими и выделяет кружком.
5. Построение нового опорного плана
Переход к новому плану проводится пересчетом симплексной таблицы по методу Жордана-Гаусса. Сначала заменим переменные в базисе, т.е. вместо 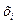 в базис войдет переменная
в базис войдет переменная 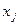 , соответствующая направляющему столбцу.
, соответствующая направляющему столбцу.
Разделим все элементы ведущей строки предыдущей симплексной таблицы на разрешающий элемент и результаты деления занесем в строку следующей симплексной таблицы, соответствующую введенной в базис переменной 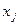 . В результате этого на месте разрешающего элемента в следующей симплексной таблице будем иметь 1, а в остальных клетках j столбца, включая клетку столбца индексной строки, записываем нули. Остальные новые элементы
. В результате этого на месте разрешающего элемента в следующей симплексной таблице будем иметь 1, а в остальных клетках j столбца, включая клетку столбца индексной строки, записываем нули. Остальные новые элементы
нового плана находятся по правилу прямоугольника: 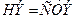 -
- 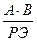 ,
,
где 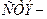 элемент старого плана,
элемент старого плана, 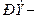 разрешающий элемент,
разрешающий элемент,
А и В - элементы старого плана, образующие прямоугольник с элементами 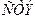 и
и 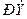 .
.
6. Полученный новый опорный план опять проверяется на оптимальность в соответствии с этапом 3 алгоритма.
При решении задачи линейного программирования на минимум целевой функции, признаком оптимальности плана является отрицательные значения всех коэффициентов индексной строки симплексной таблицы.
Если в направляющем столбце все коэффициенты 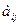
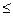 0, то функция цели
0, то функция цели 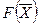 неограниченна на множестве допустимых планов, т.е.
неограниченна на множестве допустимых планов, т.е. 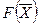
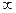 и задачу решить нельзя.
и задачу решить нельзя.
Если в столбце симплексной таблицы содержатся два или несколько одинаковых наименьших значения, то новый опорный план будет вырожденным (одна или несколько базисных переменных станут равными нулю). Вырожденные планы могут привести к зацикливанию, т.е. многократному повторению процесса вычислений, не позволяющему завершить задачу. С целью исключения этого для выбора направляющей строки используют способ Креко, который заключается в следующем. Делим элементы строк, имеющие одинаковые наименьшее значение 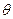 , на предполагаемые разрешающие элементы, а результаты заносим в дополнительные строки. За ведущую строку выбирается та, в которой раньше встречается меньшее число при чтении таблицы слева направо по столбцам.
, на предполагаемые разрешающие элементы, а результаты заносим в дополнительные строки. За ведущую строку выбирается та, в которой раньше встречается меньшее число при чтении таблицы слева направо по столбцам.
Если в оптимальный план вошла дополнительная переменная 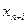 , то при реализации такого плана имеются недоиспользованные ресурсы
, то при реализации такого плана имеются недоиспользованные ресурсы 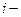 гo вида в количестве, полученном в столбце свободных членов симплексной таблицы.
гo вида в количестве, полученном в столбце свободных членов симплексной таблицы.
Если в индексной строке симплексной таблицы оптимального плана находится нуль, принадлежащий свободной переменной, не вошедшей в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов. Свободную переменную, соответствующую указанному столбцу, можно внести в базис, выполнив соответствующие этапы алгоритма. В результате будет получен второй оптимальный план с другим набором базисных переменных.
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ СИМПЛЕКСНЫМ ДЕТОДОМ.
Торговое предприятие, располагающее материально-денежными ресурсами, реализует три группы товаров А, В и С. Плановые нормативы затрат ресурсов на тыс. руб. товарооборота, прибыль от продажи товаров на тыс. руб. товарооборота, а также объем ресурсов заданы в таблице 2.
Определить плановый объем продажи и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.
Таблица 2
| Виды материально-денежных ресурсов | Норма затрат материально-денежных ресурсов на ед. товарооборота, тыс. руб. | Объём ресурсов
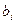
| ||
| А _ группа _ | В группа | С группа | ||
| Рабочее время продавцов, чел./ч | 0, 1 | 0, 2 | 0, 4 | |
| Площадь торговых залов, м2 | 0, 05 | 0, 02 | 0, 02 | |
| Площадь складских помещений, м2 | ||||
| Прибыль, т.руб. | max |
1.Запишем математическую модель задачи.
Определить 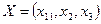 , который удовлетворяет условиям
, который удовлетворяет условиям
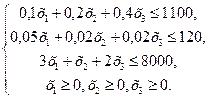
и обеспечивают максимальное значение целевой функции
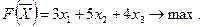
Для построения первого опорного плана систему неравенств, приведем к системе уравнений.
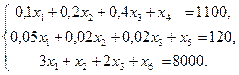
В матрице этой системы уравнений 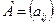 имеет:
имеет:
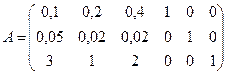
Векторы 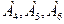 - линейно независимы, так как определитель, составленный из компонент этих векторов, отличен от нуля:
- линейно независимы, так как определитель, составленный из компонент этих векторов, отличен от нуля:
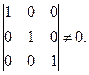
Соответствующие этим векторам переменные 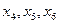 будут базисными.
будут базисными.
Решим систему уравнений относительно базисных переменных.
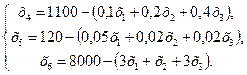
Функцию цели запишем в виде:
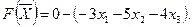
2.Полагая, что свободные переменные  =0,
=0,  =0,
=0, 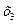 =0, получим первый опорный план
=0, получим первый опорный план
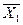 =(0, 0, 01100, 120, 8000), F
=(0, 0, 01100, 120, 8000), F 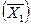 = 0, в котором базисные переменные
= 0, в котором базисные переменные 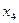 =1100,
=1100, 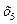 =120,
=120, 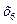 =8000,
=8000,
следовательно товары не продаются и прибыль равна нулю, а ресурсы не используются.
Заносим первый опорный план 1 в симплексную таблицу 3.
| План | Базисные переменные | Ресурсы плана | Значения коэффициентов при переменных |  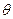
| |||||
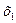
| 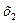
| 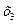
| 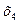
| 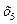
| 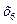
| ||||
| I план | 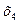
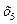
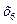
| 1100 120 8000 | 0, 1 0, 05 3 | 0, 2 0, 02 1 | 0, 4 0, 02 2 | 0 1 0 | |||
| Инд. Строка | 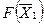
| -3 | -5 | -4 | |||||
| II план | 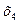
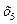
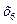
| 5500 10 2500 | 0, 5 0, 04 2, 5 | -0, 02 0 | -0, 1 -5 | ||||
| Инд. Строка | 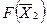
| -0, 5 | |||||||
| III план | 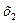
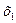
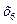
| 5375 250 1 875 | 2, 25 -0, 5 1, 25 | 6, 25 -2, 5 1, 25 | -12, 5 25 -62, 5 | 0 0 | |||
 Инд. строка Инд. строка
| 
| 5, 75 | 23, 75 | 12, 5 |
Симплексная таблица 3
Первый опорный план 1 не оптимальный, так как в индексной строке находятся отрицательные коэффициенты - -3, -5, -4.
За ведущий столбец выберем столбец, соответствующий переменной 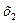 , так как сравнивая по модулю имеем:
, так как сравнивая по модулю имеем:
|- 5| >  |- 3I, |- 4I} Рассчитываем значения 9 по строкам, как частное от деления
|- 3I, |- 4I} Рассчитываем значения 9 по строкам, как частное от деления 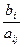 и выбираем наименьшее:
и выбираем наименьшее:
|