Постановка задачи. В симплекс – методе, рассмотренном в разделе 2.5., при осуществлении последовательных итераций используются процедуры преобразования текущей К – матрицы

В симплекс – методе, рассмотренном в разделе 2.5., при осуществлении последовательных итераций используются процедуры преобразования текущей К – матрицы методом Жордана – Гаусса. Для проведения таких вычислений на ПК требуется большой объем оперативной памяти, которая, в отличие от долговременной памяти, содержит те параметры задачи, с которыми производятся вычисления на данной итерации. При реализации симплекс – метода на S – й итерации необходимо хранить в оперативной памяти матрицу, содержащую (m+1) строку и (n+2) столбца.

Алгоритм симплекс – метода можно модифицировать так, чтобы текущая матрица, которая должна храниться в оперативной памяти, имела размеры

(m x m)

Пусть требуется решить следующую ЗЛП:

(2.89)

(2.90)

(2.91)

(2.92)

или в матричной форме

Пусть задача (2.89) – (2.91) решается симплекс-методом. Рассмотрим S -ю итерацию симплекс-метода.

Известна текущая К -матрица:

(2.93)

и определяемый ею опорный план

(2.94)

Векторы-столбцы

образуют базисную (единичную) подматрицу в матрице .

Следовательно, столбцы исходной матрицы

образуют базисную подматрицу в матрице , на месте i -й итерации в матрице

Следовательно, можно записать, что

(2.95)

или

(2.96)

(2.97)

где –матрица, обратная к базисной подматрице

Матрицу называют обращенным базисом.

Основные расчетные формулы модифицированного алгоритма.

Основным содержанием итерации симплекс-метода является построение нового базиса

,

отличающегося лишь одним столбцом от старого базиса .

Для перехода от старого базиса к новому необходимо знать: К -номер вектора, вводимого в базис, для которого

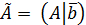
векторы и, с помощью которых находится номер

вектора, выводимого из базиса:.

Как следует из формул (2.96) – (2.97), для определения этих параметров достаточно знать исходную матрицу 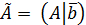, вектор , текущий обращенный базис и вектор .

Действительно,

(2.98)

(2.99)

Получим формулу, связывающую обращенный базис с базисом .

Пусть и

- базисные подматрицы матрицы А, соответствующие соседним итерациям.

Очевидно, что базис отличается от базиса только одним столбцом

Далее очевидно, что

(2.100)

Откуда и (2.101)

где

(2.102)

и

(2.103)

Итак, новый обращенный базис можно вычислять по формуле

(2.104)

Так как исходный базис обычно представляет собой единичную матрицу, то

,

Тогда

(2.105)

(2.106)