Случайные величины. Способы их задания

Случайная величина – это переменная величина, которая принимает различные значения в зависимости от случайных обстоятельств с определенными вероятностями для каждого значения. Случайные величины бывают дискретные и непрерывные.

Случайная величина X считается заданной, если известен закон ее распределения, под которым понимают определенное соотношение между значениями случайной величины и соответствующимиим вероятностями ().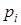

Закон распределения может быть задан:

а) таблично, с указанием всех значений случайной величины и соответствующих им вероятностей, причем сумма всех вероятностей равна единице, то есть

;

б) аналитически, с помощью интегральной функции (функции распределения вероятностей) и/или дифференциальной функции (плотнос­ти распределения вероятностей) ;

в) графически, в виде графиков интегральной (для дискретной и непрерывной случайных величин) и/или дифференциальной (для непрерывной случайной величины) функций или в виде полигона (для дискретной случайной величины).

Интегральная функция может быть выражена через дифференциальную:

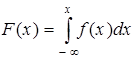
Вероятность попадания непрерывной случайной величины в интервал (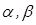) рассчитывается по одной из следующих формул:

;

.

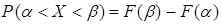Вероятность попадания случайной величины в интервал (a, b) графически можно интерпретировать как площадь под кривой распределения, ограниченной слева прямой 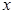= 1/2 и справа – 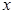= 3/2. Построим график кривой распределения (рис.1) и покажем искомую вероятность.

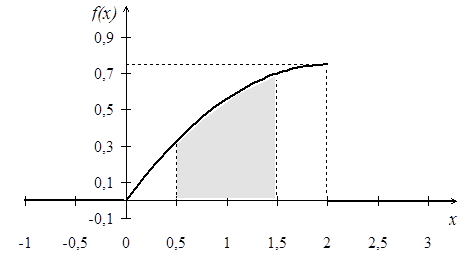
Рис.1

График функции 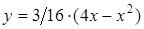– парабола (рис.1), ветви которой направлены вниз и пересекают ось абсциссв точках 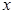= 0 и 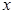= 4, вершина параболы находится в точке .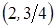