Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Числовые характеристики случайной величины
|
|
Основными числовыми характеристиками случайной величины X являются математическое ожидание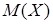 
, дисперсия D (X), среднее квадратическое отклонение 
.
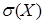Математическое ожидание случайной величины – это среднее значение случайной величины, взвешенное по вероятностям.
Для дискретной случайной величины математическое ожидание вычисляется по формуле:
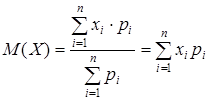, так как 
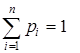, то есть 
.
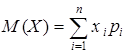Для непрерывной случайной величины:
.
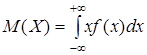Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, то есть
D (X)=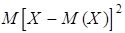 
.
Преобразуем это выражение, используя свойства математического ожидания, получим D (X) =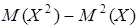 
, то есть дисперсия случайной величины равна математическому ожиданию квадрата случайной величины без квадрата ее математического ожидания. Итак:
D (X) = 
– для дискретной случайной величины;
D (X) =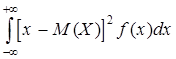 
– для непрерывной случайной величины;
D (X) = 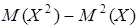– для любой случайной величины.
Средним квадратическим отклонением случайной величины называют арифметическое значение квадратного корня из ее дисперсии, то есть
.
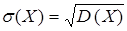Дисперсия и среднее квадратическое отклонение характеризуют вариацию (колеблемость) значений случайной величины около ее среднего значения. Так, показывает, на сколько в среднем отклоняются значения случайной величины от ее математического ожидания.
Обобщением основных числовых характеристик случайной величины является понятие моментов случайной величины.
Начальным моментом k-го порядка случайной величины называют математическое ожидание величины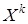 
: 
.
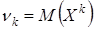Начальный момент дискретной случайной величины: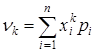 
.
Начальный момент непрерывной случайной величины: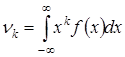 
.
Центральным моментом k-го порядка случайной величины называют математическое ожидание величины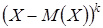 
: 
.
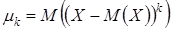Центральный момент дискретной случайной величины: 
.
Центральный момент непрерывной случайной вел-ны: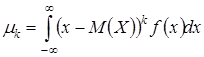 
.
Начальный момент первого порядка представляет собой математическое ожидание, а центральный момент второго порядка – дисперсию случайной величины.
Нормированный центральный момент третьего порядка служит характеристикой «скошенности» или асимметрии распределения (коэффициент асимметрии):
.
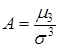Нормированный центральный момент четвертого порядка служит характеристикой «островершинности» или «плосковершинности» распределения (коэффициент эксцесса):
.
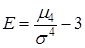Величины А и Е характеризуют степень отличия функции распределения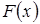 
от функции распределения стандартного нормального распределения, для которого коэффициенты асимметрии и эксцесса равны нулю: 
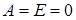. Левосторонняя асимметрия: 
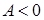, правосторонняя асимметрия: 
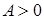. Если 
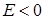, то кривая плотности распределения 
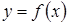имеет более плоскую вершину, чем кривая плотности нормального распределения.
Введем понятие различных операций над случайными величинами.
Пусть имеются две случайные величины X и Y, заданные следующими законами распределения:
| xi | x 1 | x 2 | … | xi | … | xn | yj | y 1 | y 2 | … | yj | … | yk | ||
| pi | p 1 | p 2 | … | рi | … | pn | ; | p’j | p’ 1 | p’ 2 | … | р’j | … | p’k | ; |
причем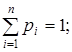 
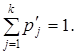
Случайной величиной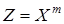 
называют такую случайную величину, возможные значения которой равны 
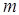- й степени значений случайной величины X, а соответствующие вероятности не изменяются. Закон распределения случайной величины Z будет иметь вид:
| 
| 
| … | 
| … | 
| |
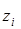
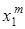
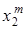
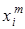
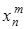
| pi | p 1 | p 2 | … | рi | … | pn | , |
Суммой (разностью, произведением) случайных величин X и Y называют случайную величину Z, возможные значения которой равны соответственно сумме (разности, произведению) каждого значения случайной величины X с каждым значением случайной величины Y, а соответствующие вероятности перемножаются.
Например, закон распределения случайной величины Z = X + Y имеет вид:
| zi |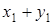 
| 
| … | 
| 
| … | 
| … | 
| |
| 
| 
| … | 
| 
| … | 
| … | 
| ; |
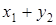
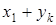
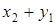
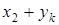
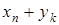
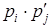
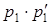
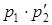
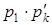
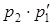
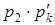
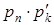
причем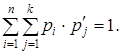 
Пример 1. Случайная величина X имеет распределение:
| xi | ||||||
| pi | 0, 1 | 0, 3 | 0, 3 | 0, 2 | 0, 1 | . |
Найти характеристики случайной величины.
Решение. Воспользуемся формулами для дискретной случайной величины.
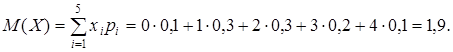
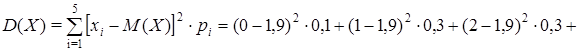
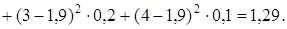
Дисперсию случайной величины можно рассчитать и по формуле:
D (X) = .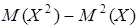
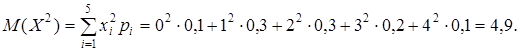
D (X) = 4, 9 – (1, 9)2 = 4, 9 – 3, 61 = 1, 29.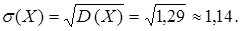 
Среднее квадратическое отклонение характеризует колеблемость значений случайной величины около математического ожидания.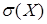 
» 1, 14 означает, что каждое значение данной случайной величины отклоняется от математического ожидания (от среднего значения) в среднем на 1, 14.
Пример 2. Случайная величина X задана следующим распределением:
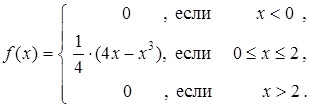
Найти характеристики случайной величины.
Решение. Воспользуемся формулами для непрерывной случайной величины.
= 
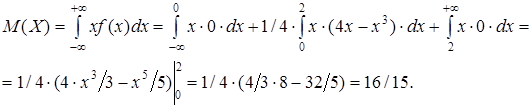
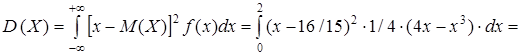
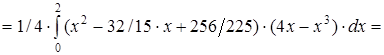
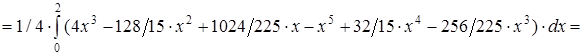
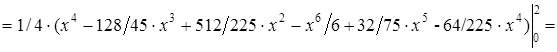
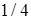(16 – 1024/45 + 2048/225 – 32/3 + 1024/75–1024/225) = 44/225.
Проще вычислить дисперсию по формуле:
D (X) = .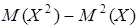
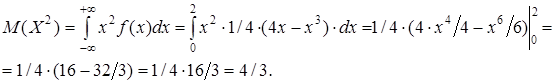
D (X) = 4/3 – (16/15)2 = 44/225.
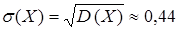(каждое значение случайной величины отклоняется от математического ожидания в среднем на 0, 44).
Пример 3. Случайные величины X и Y заданы следующими распределениями:
| xi | yj | ||||||||||
| pi | 0, 1 | 0, 5 | 0, 2 | 0, 2 | ; | p j | 0, 6 | 0, 4 | . |
Составить закон распределения случайной величины Z = X – Y.
На этом примере проверить справедливость свойства дисперсии разности двух независимых случайных величин.
Решение: 1) составим закон распределения случайной величины Z = X – Y.
| zi | 1 – 0 | 1 – 1 | 2 – 0 | 2 – 1 | 3 – 0 | 3 – 1 | 5 – 0 | 5 – 1 | |
| pi × pj | 0, 06 | 0, 04 | 0, 30 | 0, 20 | 0, 12 | 0, 08 | 0, 12 | 0, 08 | ; |
или:
| zi | |||||||
| 0, 04 | 0, 26 | 0, 38 | 0, 12 | 0, 08 | 0, 12 | . |
2) найдем характеристики случайных величин X, Y, Z.
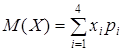= 0, 1 + 1 + 0, 6 + 1 = 2, 7.
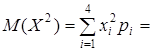0, 1 + 2 + 1, 8 + 5 = 8, 9.
D (X) = 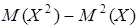= 8, 9 – (2, 7)2 = 1, 61.
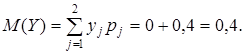
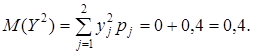
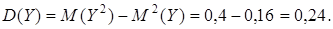
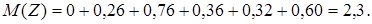
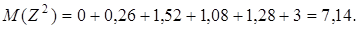
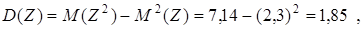то есть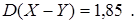 
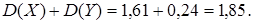
Отсюда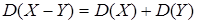 
.