
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Составить уравнение плоскости, проходящей через точку А и перпендикулярно вектору .
|
|
7.1. А (2, 5, -3), В (7, 8, -1), С(9, 7, 4).
7.2. А (7, -5, 0), В (8, 3, -1), С(8, 5, 1).
7.3. А (5, 3, -1), В (0, 0, -3), С(5, -1, 0).
7.4. А (0, 7, -9), В (-1, 8, -11), С(-4, 3, -12).
7.5. А (0, -8, 10), В (-5, 5, 7), С(-8, 0, 4).
7.6. А (-3, 1, 0), В (6, 3, 3), С(9, 4, -2).
7.7. А (-7, 1, -4), В (8, 11, -3), С(9, 9, -1).
7.8. А (3, -3, -6), В (1, 9, -5), С(6, 6, -4).
7.9. А (1, -1, 5), В (0, 7, 8), С(-1, 3, 8).
7.10. А (-3, 7, 2), В (3, 5, 1), С(4, 5, 3).
7.11. А (0, -3, 5), В (-7, 2, 6), С(-3, 2, 4).
7.12. А (1, 9, -4), В (5, 7, 1), С(3, 5, 0).
7.13. А (1, -1, 8), В (-4, -3, 10), С(-1, -1, 7).
7.14. А (7, -5, 1), В (5, -1, -3), С(3, 0, -4).
7.15. А (4, -2, 0), В (1, -1, -5), С(-2, 1, -3).
7.16. А (1, 0, -2), В (2, -1, 3), С(0, -3, 2).
7.17. А (-1, 3, 4), В (-1, 5, 0), С(2, 6, 1).
7.18. А (-8, 0, 7), В (-3, 2, 4), С(-1, 4, 5).
7.19. А (-3, 5, -2), В (-4, 0, 3), С(-3, 2, 5).
7.20. А (-2, 0, -5), В (2, 7, -3), С(1, 10, -1).
7.21. А (-7, 0, 3), В (1, -5, -4), С(2, -3, 0).
7.22. А (5, -1, 2), В (2, -4, 3), С(4, -1, 3).
7.23. А (0, -2, 8), В (4, 3, 2), С(1, 4, 3).
7.24. А (-10, 0, 9), В (12, 4, 11), С(8, 5, 15).
7.25. А (2, 1, 7), В (9, 0, 2), С(9, 2, 3).
7.26. А (1, 0, -6), В (-7, 2, 1), С(-9, 6, 1).
7.27. А (-4, -2, 5), В (3, -3, -7), С(9, 3, -7).
7.28. А (1, -5, -2), В (6, -2, 1), С(2, -2, -2).
7.29. А (-3, -1, 7), В (0, 2, -6), С(2, 3, -5).
7.30. А (-1, 2, -2), В (13, 14, 1), С(14, 15, 2).
8. Даны четыре точки A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3), D(x4, y4, z4). 
Найти: а) уравнение плоскости, проходящей через точки А, В, С;
б) расстояние от точки Д до плоскости АВС;
в) угол между плоскостью АВС и плоскостью 5x-3y+7z-3=0.
8.1. А (1, -1, 2), В (2, 1, 2), С (1, 1, 4), Д (6, -3, 8).
8.2. А (-3, -5, 6), В (2, 1, -4), С (0, -3, -1), Д (-5, 2, -8).
8.3. А (1, 3, 0), В (4, -1, 2), С (3, 0, 1), Д (-4, 3, 5).
8.4. А (-1, 2, 4), В (-1, -2, -4), С (3, 0, -1), Д (7, -3, 1).
8.5. А (1, 2, -3), В (1, 0, 1), С (-2, -1, 6), Д (0, -5, -4).
8.6. А (1, 2, 0), В (1, -1, 2), С (0, 1, -1), Д (-3, 0, 1).
8.7. А (4, -1, 3), В (-2, 1, 0), С (0, -5, 1), Д (3, 2, -6).
8.8. А (-3, 4, -7), В (1, 5, -4), С (-5, -2, 0), Д (2, 5, 4).
8.9. А (1, 1, -1), В (2, 3, 1), С (3, 2, 1), Д (5, 9, -8).
8.10. А (1, 1, 2), В (-1, 1, 3), С (2, -2, 4), Д (-1, 0, -2).
8.11. А (1, 2, 0), В (3, 0, -3), С (5, 2, 6), Д (8, 4, -9).
8.12. А (-2, 0, -4), В (-1, 7, 1), С (4, -8, -4), Д (1, -4, 6).
8.13. А (5, 2, 0), В (2, 5, 0), С (1, 2, 4), Д (-1, 1, 1).
8.14. А (-1, -5, 2), В (-6, 0, -3), С (3, 6, -3), Д (-10, 6, 7).
8.15. А (7, 2, 4), В (7, -1, -2), С (3, 3, 1), Д (-4, 2, 1).
8.16. А (1, 3, 6), В (2, 2, 1), С (-1, 0, 1), Д (-4, 6, -3).
8.17. А (-4, 2, 6), В (2, -3, 0), С (-10, 5, 8), Д (-5, 2, -4).
8.18. А (2, 1, 4), В (-1, 5, -2), С (-7, -3, 2), Д (-6, 3, 6).
8.19. А (0, -1, -1), В (-2, 3, 5), С (1, -5, -9), Д (-1, -6, 3).
8.20. А (2, -1, -2), В (1, 2, 1), С (5, 0, -6), Д (-10, 9, -7).
8.21. А (14, 4, 5), В (-5, -3, 2), С (-2, -6, -3), Д (-2, 2, -1).
8.22. А (2, -1, 2), В (1, 2, -1), С (3, 2, 1), Д (-4, 2, 5).
8.23. А (2, 3, 1), В (4, 1, -2), С (6, 3, 7), Д (7, 5, -3).
8.24. А (1, 5, -7), В (-3, 6, 3), С (-2, 7, 3), Д (-4, 8, -12).
8.25. А (-1, 2, -3), В (-2, 1, 0), С (0, -5, 1), Д (3, 2, -6).
8.26. А (1, -1, 1), В (-2, 0, 3), С (2, 1, -1), Д (2, -2, -4).
8.27. А (1, 0, 2), В (1, 2, -1), С (2, -2, 1), Д (2, 1, 0).
8.28. А (3, 10, -1), В (-2, 3, -5), С (-6, 0, -3), Д (1, -1, 2).
8.29. А (0, -3, 1), В (-4, 1, 2), С (2, -1, 5), Д (3, 1, -4).
8.30. А (-2, -1, -1), В (0, 3, 2), С (3, 1, -4), Д (-4, 7, 3).
Прямая L1 задана общими уравнениями.
Найти: а) канонические и параметрические уравнения прямой L1;
б) найти угол между прямой L1 и прямой L2: 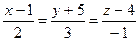 ;
;
В) найти расстояние от точки А(1, -3, 4) до прямой L1.
9.1. L1: 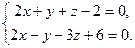
| 9.4. L1: 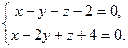
|
9.2. L1: 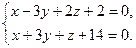
| 9.5. L1: 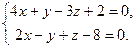
|
9.3. L1: 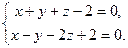
| 9.6. L1: 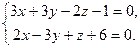
|
9.7. L1: 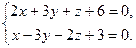
| 9.19.L1: 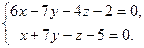
|
9.8. L1: 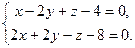
| 9.20. L1: 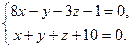
|
9.9. L1: 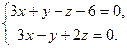
| 9.21.L1: 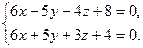
|
9.10. L1: 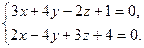
| 9.22. L1: 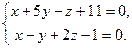
|
9.11. L1: 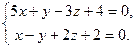
| 9.23. L1: 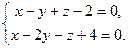
|
9.12. L1: 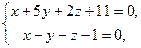
| 9.24. L1: 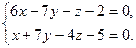
|
9.13. L1: 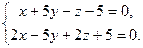
| 9.25. L1: 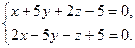
|
9.14. L1: 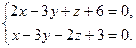
| 9.26.L1: 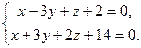
|
9.15. L1: 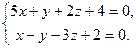
| 9.27.L1: 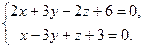
|
9.16. L1: 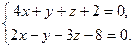
| 9.28.L1: 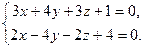
|
9.17. L1: 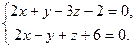
| 9.29.L1: 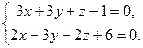
|
9.18. L1: 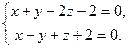
| 9.30.L1: 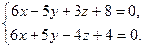
|
Найти точку пересечения прямой и плоскости.
10.1. 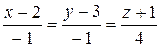 ,
, 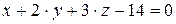 .
.
10.2. 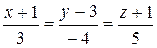 ,
, 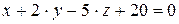 .
.
10.3. 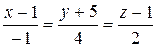 ,
, 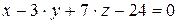 .
.
10.4. 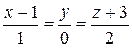 ,
, 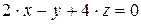 .
.
10.5. 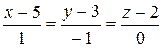 ,
, 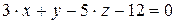 .
.
10.6. 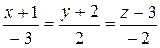 ,
, 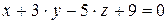 .
.
10.7. 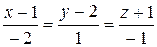 ,
, 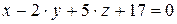 .
.
10.8. 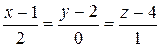 ,
, 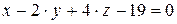 .
.
10.9. 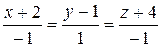 ,
, 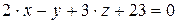 .
.
10.10. 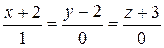 ,
, 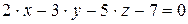 .
.
10.11. 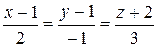 ,
, 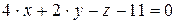 .
.
10.12. 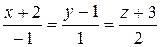 ,
, 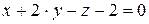 .
.
10.13. 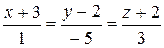 ,
, 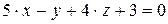 .
.
10.14. 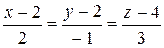 ,
, 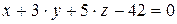 .
.
10.15. 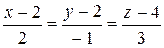 ,
, 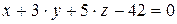 .
.
10.16. 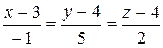 ,
, 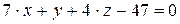 .
.
10.17. 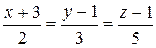 ,
, 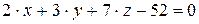 .
.
10.18. 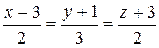 ,
, 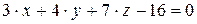 .
.
10.19. 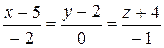 ,
, 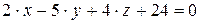 .
.
10.20. 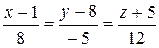 ,
, 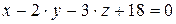 .
.
10.21. 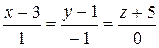 ,
, 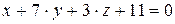 .
.
10.22. 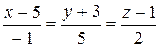 ,
, 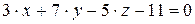 .
.
10.23. 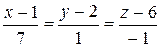 ,
, 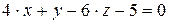 .
.
10.24. 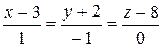 ,
, 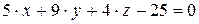 .
.
10.25. 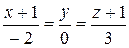 ,
, 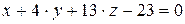 .
.
10.26. 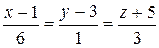 ,
, 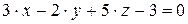 .
.
10.27. 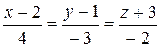 ,
, 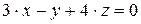 .
.
10.28. 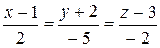 ,
, 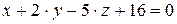 .
.
10.29. 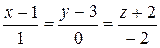 ,
, 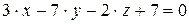 .
.
10.30. 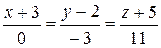 ,
, 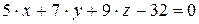 .
.